部分構造の共有を観測するdata-reify
この記事は Haskell Advent Calendar 2017 の12/21(木)の記事です。
昨年の Haskell Advent Calendar 2016 の記事 Hash-consingのためのinternパッケージ では、同値な部分構造を共通化するテクニック hash-consing および、そのためのHaskellライブラリ intern の紹介を行いました。
今回は、これに若干近い方向性のライブラリとして、部分構造の共有を観測して明示的に扱うライブラリ data-reify について紹介しようと思います。
部分構造の共有の例
Haskellでのプログラミングでは、部分構造を共有したデータ構造や、さらに遅延評価を利用した循環構造を持ったデータ構造を多用します。
例えば、ご存知のように
repeat :: a -> [a]
repeat x = xs
where
xs = x : xs
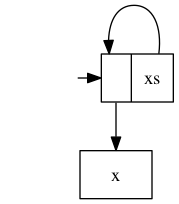
という関数の生成する無限リストは、(評価後には)メモリ上では以下のような循環構造を持って表現されます。
同様に論理式を表す以下のようなデータ型と値を考えてみましょう。
data Formula
= Atom Int
| Not Formula
| And Formula Formula
| Or Formula Formula
| Imply Formula Formula
deriving (Show)
equiv :: Formula -> Formula -> Formula
equiv p q = And (p `Imply` q) (q `Imply` p)
sample :: Formula
sample = And p q `equiv` Not (Or (Not p) (Not q))
where
p = Atom 0
q = Atom 1
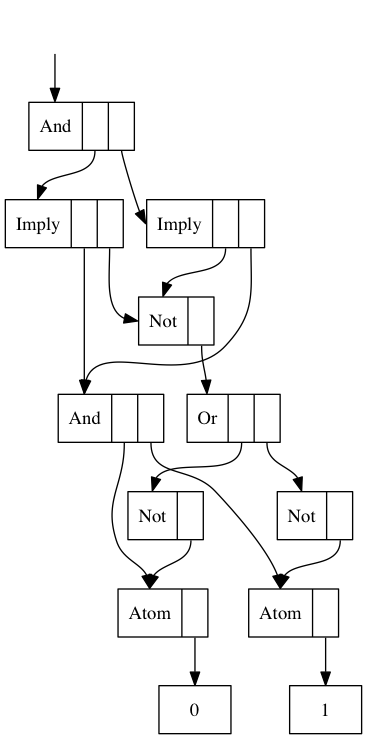
この値は(評価後には)メモリ上では以下のように表現されます。 And p q と Not (Or (Not p) (Not q)) とが 2つの Imply の間で共有されていることが分かります。
Haskellでの問題
Haskell では実際の実行時のメモリ上では上記のような部分構造の共有が行われていますが、純粋関数型言語としてのHaskellは、(オブジェクト指向言語のオブジェクトなどと異なり)値に同一性の概念がないため、このような共有が行われていることを観測したり、それに基いて処理を行うことは出来ません。
そのため、共有を意識した処理を行いたい場合、データ構造として上記のようなHaskellとして自然な表現を用いることはできず、共有を明示的に扱うデータ構造を用いる必要があります。
論理式の例であれば共有はあるけれど循環はないため、昨年 Hash-consingのためのinternパッケージ で紹介した intern パッケージのような手法を用いる方法があります(その代わり intern を用いると等価な部分式はすべて共有されてしまいますが)。
一方で、上記の循環リストの例では intern パッケージのような手法をそのまま用いることはできず、グラフ構造を明示的に扱う必要が出てきてしまい、非常に煩雑になります。
どんなときにそんな処理が必要になるのかと思われるかも知れませんが、上記の論理式の例などのように、複雑な演算子をより単純なデータ構築子の組み合わせで表現するということを行っていくと、データ構造は多くの共有を含む結果となり、共有を意識せずに単純に再帰で処理すると、多数の重複した計算を行ってしまって非効率になってしまいます。
また、循環データ構造の方に関しても、埋め込みDSLの解釈などで、少しメタなことをしようとするとやはり共有を意識した処理を行いたい場合があります。 例えば、埋め込みDSLで書かれた記述からHDLを生成する Lava では、以下の例のように、順序回路の記述として delay 関数を挟んだ循環が現れることがあり、ここから有限のHDLを生成するには、やはり共有を明示的に意識した処理を行う必要があります。(もちろんそのような循環を使わないような埋め込みDSLの設計も考えられますが、確実に記述が煩雑なものにってしまいます)
toggle :: Bit -> Bit
toggle change = out
where
out' = delay low out
out = xor2 (change, out')
(コード例は『関数プログラミングの楽しみ』 の「第8章 Lava: 関数によるハードウェア記述」 p.172 より抜粋)
data-reify パッケージのインターフェース
data-reify パッケージ はこのような問題を解決するためのパッケージで、Haskellの通常のデータ型の値を受け取り、それをグラフのデータ型に変換して返す機能を提供しています。
まず、 これを書いている時点での最新版である data-reify-0.6.1 の Data.Reify の提供しているインターフェースを見てみましょう。
{-# LANGUAGE TypeFamilies #-}
type Unique = Int
data Graph e = Graph [(Unique, e Unique)] Unique
class MuRef a where
type DeRef a :: * -> *
mapDeRef
:: Applicative f
=> (forall b. (MuRef b, DeRef a ~ DeRef b) => b -> f u)
-> a -> f (DeRef a u)
reifyGraph :: MuRef s => s -> IO (Graph (DeRef s))
メインの機能は reifyGraph ですが、まずは補助的な定義を見ていきます
グラフの表現
type Unique = Int
data Graph e = Graph [(Unique, e Unique)] Unique
Unique はグラフの頂点を表す値で、 Graph e は [(Unique, e Unique)] として表されたグラフとその中の一つの頂点 Unique のペアになっています。
グラフ部分の [(Unique, e Unique)] は、親頂点に対して、子頂点のコレクションを対応付ける連想リストとして表現されていて、 e が子のコレクションを抽象化する型構築子という感じです。 ただし、後述するように、 e は単なる子のコレクションというだけではなく、親頂点に関する他の情報も持ち得ます。
グラフのこの表現は containers の Data.Graph とか IntMap など、グラフ処理に用いる他のデータ構造へと変換しやすいことを念頭に設計されています。
MuRef 型クラス
class MuRef a where
type DeRef a :: * -> *
mapDeRef
:: Applicative f
=> (forall b. (MuRef b, DeRef a ~ DeRef b) => b -> f u)
-> a -> f (DeRef a u)
次に型クラス MuRef ですが、これがグラフに変換できる型を表す型クラスです。 Graph の引数の e として渡すための DeRef a が関連型として定義されています。 また、 唯一のメソッドの mapDeRef は型が若干複雑ですが、 mapDeRef g a は a の中に含まれる子への参照を g :: forall b. (MuRef b, DeRef a ~ DeRef b) => b -> f u で処理した結果を集めて DeRef a u の形で返す関数です。
なお、型変数 f, u を用いた多相的な定義に一般化されていますが、reifyGraph 内で呼ばれる際にはそれぞれ IO と Unique に実体化されるので、型が複雑だと感じる方はまずは具体化した型で理解すると良いかも知れません。
mapDeRef
:: MuRef a
=> (forall b. (MuRef b, DeRef a ~ DeRef b) => b -> IO Unique)
-> a -> IO (DeRef a Unique)
また、 g の型が単純な a -> f u ではなく forall b. (MuRef b, DeRef a ~ DeRef b) => b -> f u と一般化された型になっているのは、 DeRef の型さえ一致していれば子ノードの型は別の型でも構わないこという事実を表しています。 子の型が常に 同じ a だと仮定すると、さらに以下のような型に単純化することもできます。
mapDeRef :: MuRef a => (a -> IO Unique) -> a -> IO (DeRef a Unique)
reifyGraph 関数
reifyGraph :: MuRef s => s -> IO (Graph (DeRef s))
そして、 reifyGraph は MuRef クラスのインスタンスである型の値を受け取り、グラフとグラフ中での元の値に対応するノードの情報を返します。
上でApplicative関手 f が実際には IO に具体化されると書きましたが、この関数は値の(等価性ではなく)メモリ上での同一性という純粋でない性質に依存した結果を返すので、結果は IO モナド上の計算になっています。
使用例1: 論理式
インターフェースの説明を書きましたが、これだけでは使い方が良くわからない人が多いと思うので、簡単な使用例として上で書いた論理式のグラフ表現を取り出してみましょう。
まずは、Formula データ型の各構築子毎に、子の現れる部分を型変数に置き換えたデータ型を定義します。
{-# LANGUAGE DeriveFunctor #-}
{-# LANGUAGE DeriveFoldable #-}
{-# LANGUAGE DeriveTraversable #-}
data FormulaF a
= AtomF Int
| NotF a
| AndF a a
| OrF a a
| ImplyF a a
deriving (Show, Functor, Foldable, Traversable)
そして、それを DeRef 結果として用いる MuRef インスタンスを定義します。 部分式を f の適用結果で置き換えるには、Applicative関手に関するコンビネータを用いると簡潔に書くことができます。
instance MuRef Formula where
type DeRef Formula = FormulaF
mapDeRef f phi =
case phi of
Atom p -> pure (AtomF p)
Not p -> NotF <$> f p
And p q -> AndF <$> f p <*> f q
Or p q -> OrF <$> f p <*> f q
Imply p q -> ImplyF <$> f p <*> f q
そして、上の例に対して reifyGraph を適用してみます。
*Main> g <- reifyGraph sample
*Main> g
let [(1,AndF 2 10),(10,ImplyF 6 3),(2,ImplyF 3 6),(6,NotF 7),(7,OrF 8 9),(9,NotF 5),(8,NotF 4),(3,AndF 4 5),(5,AtomF 1),(4,AtomF 0)] in 1
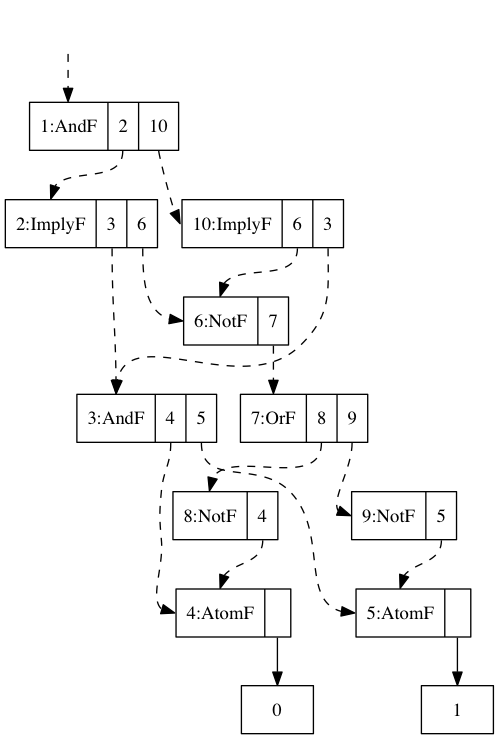
この結果は以下の図のような構造を表しています。 頂点番号による明示的な頂点の参照となった部分については破線で描いてみています。
これは最初と同じ構造ですが、共有された部分構造に対して同じ頂点番号が振られることで、共有されていることが明示的に分かるようになっています。 このグラフに対して処理を行えば、共有部分式に対する重複した処理を行わずに済みます。
型の不動点
ところで、気づいたとは思いますが、 Formula は FormulaF の不動点になっています。 そして、 Formula をそのように定義すると、mapDeRef を非常に一般的に定義することができます。
newtype Formula2 = Formula2 (FormulaF Formula2)
instance MuRef Formula2 where
type DeRef Formula2 = FormulaF
mapDeRef f (Formula2 phi) = traverse f phi
実装
ここで実装についても簡単に触れておくと、クロージャ(未評価のサンクや評価済の値などのメモリ上のオブジェクトを指すHaskell用語)の同一性を判定するために System.Mem.StableName の StableName を用いています。
以下の短いコードが本質的な実装部分です。
reifyGraph :: (MuRef s) => s -> IO (Graph (DeRef s))
reifyGraph m = do rt1 <- newMVar M.empty
rt2 <- newMVar []
uVar <- newMVar 0
root <- findNodes rt1 rt2 uVar m
pairs <- readMVar rt2
return (Graph pairs root)
findNodes :: (MuRef s)
=> MVar (IntMap [(DynStableName,Int)])
-> MVar [(Int,DeRef s Int)]
-> MVar Int
-> s
-> IO Int
findNodes rt1 rt2 uVar j | j `seq` True = do
st <- makeDynStableName j
tab <- takeMVar rt1
case mylookup st tab of
Just var -> do putMVar rt1 tab
return $ var
Nothing ->
do var <- newUnique uVar
putMVar rt1 $ M.insertWith (++) (hashDynStableName st) [(st,var)] tab
res <- mapDeRef (findNodes rt1 rt2 uVar) j
tab' <- takeMVar rt2
putMVar rt2 $ (var,res) : tab'
return var
findNodes _ _ _ _ = error "findNodes: strictness seq function failed to return True"
若干の補足を加えるとこんな感じです。
-
StableNameの型パラメータ部分を隠すためにDynStableNameという型にラップしてある -
rt1 :: MVar (IntMap [(DynStableName,Int)])は DynStableName から 頂点番号への写像 (IntMapとリストでハッシュテーブルを表現) -
rt2 :: MVar [(Int,DeRef s Int)]は構築中のグラフの情報 -
uVar :: MVar Intは頂点番号の生成用のカウンタ -
StableNameはクロージャの評価前後で異なるものになりえるので、makeDynStableNameを呼ぶ前にseqで評価済みの状態にする
使用例2: 自動微分
ところで、data-reify の他のちょっと面白かった応用例として、Haskell での自動微分のライブラリ ad があります(ここではad-4.3.4を対象とします)。 adは Edward Kmett さん作で、Haskellらしい非常に整然としたインターフェースと巧妙な実装を備えています(実用しようと思うと性能的に難がある部分もありますが……)。
自動微分の手法には、フォワードモード(ボトムアップ)自動微分、リバースモード(トップダウン)自動微分など幾つかの方法があり、特にリバースモードの自動微分は最近ではバックプロパゲーション(誤差逆伝播法)として機械学習・深層学習で広く使われています。 adパッケージではリバースモードの自動微分として Reverse と Kahn の二種類の実装を提供しています。
adパッケージでは微分対象の関数を、Doubleなどの通常の数値型の代わりに AD s (Forward Double) といった特殊な型上の関数として定義すると、
diff :: Num a => (forall s. AD s (Forward a) -> AD s (Forward a)) -> a -> agrad :: (Traversable f, Num a) => (forall s. f (AD s (Forward a)) -> AD s (Forward a)) -> f a -> f a
などの関数を使って微分できるようになっていますが、 AD s (Forward Double) などのデータ型は Num などの型クラスのインスタンスになっているため、普通の関数を書くのとほぼ同じ感覚で書くことができます。
微分対象の関数は予めグラフとして構築するのではなく、通常の関数として書く形で、条件分岐や再帰なども自由に書けるので、define-and-run ではなく define-by-run 方式と言えるでしょう。
そして、define-by-run 方式で、リバースモードの自動微分を実装しようと思うと、関数の実行時に計算履歴のグラフを構築し、勾配を計算する際にはこのグラフの最後のノードから逆に辿って各ノードの勾配を順に計算していきます。
Haskellでの自然な実装を考えると AD s (Kahn Double) 等の型の内部に、通常の計算結果の値に加えて計算履歴を木として持たせることが考えられます。ただし、木として持たせてしまうと共有の情報が失われてしまうので、中間変数が複数の経路で最終結果の計算に関わっている場合などの勾配の計算に問題が出てしまいます。
それに対して ad では、Reverseの方では unsafePerformIO を使って一種のIDを生成することで解決する手法をとり、 Kahn の方では共有の情報を data-reify を使って復元する方法が用いられています。 具体的には以下の Kahn 型に値と計算履歴の情報が格納されており、これが data-reifyの対象となっています。
-- | A @Tape@ records the information needed back propagate from the output to each input during reverse 'Mode' AD.
data Tape a t
= Zero
| Lift !a
| Var !a {-# UNPACK #-} !Int
| Binary !a a a t t
| Unary !a a t
deriving (Show, Data, Typeable)
-- | @Kahn@ is a 'Mode' using reverse-mode automatic differentiation that provides fast 'diffFU', 'diff2FU', 'grad', 'grad2' and a fast 'jacobian' when you have a significantly smaller number of outputs than inputs.
newtype Kahn a = Kahn (Tape a (Kahn a)) deriving (Show, Typeable)
instance MuRef (Kahn a) where
type DeRef (Kahn a) = Tape a
mapDeRef _ (Kahn Zero) = pure Zero
mapDeRef _ (Kahn (Lift a)) = pure (Lift a)
mapDeRef _ (Kahn (Var a v)) = pure (Var a v)
mapDeRef f (Kahn (Binary a dadb dadc b c)) = Binary a dadb dadc <$> f b <*> f c
mapDeRef f (Kahn (Unary a dadb b)) = Unary a dadb <$> f b
少しだけ意味を補足すると、各構築子は以下のような意味になっています。
-
Zeroはゼロと分かっている値を表す構築子 -
Liftは定数値を表す構築子 -
Varは入力変数を表す構築子で、値と変数インデックスを保持する -
Unaryは単項演算の適用結果を表す構築子で値a、入力値での傾き∂a/∂b、 入力値bの情報の3つの値を持つ - 同様に
Binaryは二項演算の適用結果を表す構築子で値a、第一引数に対する偏微分値∂a/∂b、第二引数の偏微分値∂a/∂c、第一引数の情報b、第二引数の情報cの4つの値を持つ
まとめ
部分構造の共有を観測するdata-reifyを紹介し、そのインターフェースと実装、論理式のデータ型を対象とした簡単な使い方、また応用例として自動微分ライブラリでadでの使用例を簡単に紹介しました。
data-reify は実装には好みの分かれるかもしれないトリックが用いられていますが、これを使うことでHaskellらしい簡潔なインターフェースを提供できることは、ちょこちょこありそうなので、そういう場合には使ってみたいですね。