この記事は理物 Advent Calendar 2022の25日目の記事です。

はじめに

メリークリスマス！クリぼっちしかいないであろう弊学科のみんなに、この記事をクリスマスプレゼントとして捧げたいと思います。冷え切った心を温めるのに一番効くのはやっぱり物理を学ぶことでしょう。

タイトルを見てわかる通り、今回は冬の風物詩「フィギュアスケート」について語ろうと思いま、、、せん。小さい時は自宅のテレビで冬は毎晩フィギュアスケートが流れていたのですが、東京で一人暮らしをし始めてからは一切見てません。（自宅のテレビを酔った勢いで破壊したというのもあります。）

ではなぜこんなタイトルにしたのか¹。それはこの記事を読めばわかるようになっています。興味のある人はぜひお付き合いください。

本記事ではまず最初に題名にある 「Haldane予想」 と呼ばれる主張について説明します。次にその主張を支持する具体的な例を2つ紹介します。1つはスピン $1/2$ の反強磁性ハイゼンベルグモデルにおける Leib-Schultz-Mattisの定理 で、もう一つが AKLTモデル についてです。ここではHaldane予想そのものの"証明"を解説することは自身の実力や記事としての読みやすさを考慮して断念しています。代わりに、予想を示す傍証となる2つの例を取り上げることにしました。

※この記事は主に田崎先生の"Physics and Mathematics of Quantum Many-Body Systems"の6、7章と、同じく田崎先生のこの講義録を参考にしています。

Haldane予想とは

Haldane予想とは、1次元反強磁性ハイゼンベルグモデルにおいてスピンの大きさ $S$ が整数 $(1,2,3,\cdots)$ のときと、半整数 $(1/2, 3/2, 5/2,\cdots)$ のときとで性質が大きく変わるというHaldaneによる主張のことをいいます。

$L$個のサイトにあるスピン $S$ からなる1次元反強磁性ハイゼンベルグモデルを考えます。スピンの大きさは $S=1/2, 1, 3/2, \cdots$ のなんでも良いとします。ハミルトニアンは以下のようになります。

\begin{align}
\hat{H} = \sum_{x=1}^L \hat{S}_x\cdot\hat{S}_{x+1}
\end{align}

ここで ${\hat{S}}_x = (\hat{S}_x^{(1)}, \hat{S}_x^{(2)}, \hat{S}_x^{(3)})$ はサイト $x$ にいるスピン演算子です。スピン同士の積が正の係数をもって入っているので、この系のエネルギーはスピンが反対を向けば下がることがわかります ² 。つまりこの系はスピンが揃いにくくなっており、それゆえこのハミルトニアンで表されるモデルを"反"強磁性と呼ぶわけです。

反強磁性ハイゼンベルグモデルのうち、 $S=1/2$ のものは厳密に解くことができます。ここでいう厳密解は、基底状態とその他のいくつかのエネルギー固有値・固有状態を書き下すことができるというものです。最初の厳密解は1931年にベーテにより、有名な「ベーテ仮設」を用いて導かれました。それ以降 $S=1/2$ の反強磁性ハイゼンベルグモデルは量子スピン系の恰好の研究対象となっています。

スピンが $S=1/2$ での厳密解から、反強磁性ハイゼンベルグモデルの低エネルギー励起について次のような性質があると考えられていました。

基底状態は一意である

基底状態と第一励起状態との間にエネルギーギャップはない

基底状態でスピン相関関数はべき的に（ゆっくりと）減衰をする

1つ目の基底状態の一意性は、大雑把には長距離秩序がなく、自発的対称性の破れがないということと同じです。この振る舞いは低温でのイジングモデルなどに見られる自発的に対称性が破れた状態が持つ性質とは対照的です。古典イジングモデルの場合、秩序が壊れるのは高温で熱ゆらぎが大きくなる場合でしたが、今回の量子スピン系では基底状態での強い"量子ゆらぎ"が原因で秩序が生まれないという風に直感的に理解できます。実は、反強磁性ハイゼンベルグモデルでの基底状態の一意性はMarshall-Lieb-Mattisの定理により保証されています。つまりスピンの大きさが整数でも半整数でも基底状態は一意であることがわかっています。

この記事で注目するのは2つ目の性質のエネルギーギャップの有無です。エネルギーギャップがないということは、基底状態のエネルギーのすぐ上に励起状態のエネルギーがあるということで、これはサイト数 $L$ が大きいところでエネルギーの差が $O(1/L)$ で小さくなるということを示しています。場の量子論の観点から、このような性質をもつ $S=1/2$ の反強磁性ハイゼンベルグモデルは自発的対称性の破れのない質量0の場の理論で説明できるそうです。ギャップがないので、粒子をいくらでも小さいエネルギーコストで励起できるということです。（さらに、相関関数のべき的な減衰に対応するのが、この場の理論での力が長距離力であるということです。）

上で述べた3つの性質はスピンの大きさに関わらず成立してもよいように思えます。スピンの大きさは直感的には粒子の回転の速さであり、量子化されたその量が整数でも半整数でも振る舞いが大きく変わることはあまりなさそうです。

しかし、Haldaneは1983年の彼の論文で驚くべき結論を導いています。反強磁性ハイゼンベルグモデルにおいて、スピンの大きさが整数と半整数の場合で性質が大きく変わるというのです。彼の主張は、スピンが半整数の場合は上で述べた3つの性質と同じ性質を持つが、整数の場合は次のように別の性質を持つというものでした。

基底状態は一意である

基底状態と励起状態の間に消えないエネルギーギャップが存在する

基底状態でのスピン相関関数は指数関数的に（速く）減衰する

1つ目の性質は半整数の場合と同じです。2つ目の性質にあるエネルギーギャップはHaldaneギャップとも呼ばれるもので、サイト数 $L$ によらず消えません。場の量子論の観点からは、スピンが整数の反強磁性ハイゼンベルグモデルは質量をもつ場と同じ振る舞いをします。真空（基底状態）から粒子を生成するのに一定のエネルギーを必要とする点（性質2）、またその力は短距離力であること（性質3）が対応しています。

スピンが整数の場合と半整数の場合の違いをまとめます。まず、統計力学の観点では、

半整数 $\leftrightarrow$ 臨界点
整数 $\leftrightarrow$ 無秩序相

という対応関係があります。この対応関係は対称性の破れや相関関数の減衰などから理解できるでしょう。³ 次に場の量子論の観点からは、

半整数 $\leftrightarrow$ 質量0の場
整数 $\leftrightarrow$ 質量をもつ場

となります。

Haldaneはこのような性質の違いを何もないところから見出したわけではないようです。この議論は2つの出所があり、一つは非線形シグマモデルの量子化、もう一つはソリトンの半古典的な量子化（？）の研究です。モデルを直接解いて示すというよりは、スピンが大きい極限での振る舞いを調べていく中で発見したというところでしょうか。何はともあれ、Haldaneによるこの主張は当時の研究者たちに衝撃を与え、"Haldane Conjecture" (Haldane予想）と呼ばれるようになりました。⁴

最後にHaldane予想の驚きポイントだけまとめておきます。

途中でも述べたように、スピンが $1/2, 1, 3/2, 2, \cdots$ と大きくなるにつれて"交互に"性質が行ったり来たりすること。（ある大きさを境にして変わるとかならまだ驚かないかも。）
スピンの大きさが整数でもスピンを徐々に傾けることでいくらでも小さい励起エネルギーを作り出せる気がするのに、実際にはギャップがあること。
スピン波理論では整数と半整数の違いは現れないこと。(でも近似を使ったりするからそこまで驚きではないかも）
フィギュアスケートのアクセルとループ（やその他整数回転のジャンプ）では難易度以外にも違いがあるということ。

次に、半整数スピンの性質を示すLieb-Schultz-Mattisの定理と、整数スピンの性質を示すAKLTモデルについて説明していきたいと思います。ここで述べたHaldane予想の傍証となる重要な結果です。

Leib-Schultz-Mattisの定理

定理の内容

Leib-Schultz-Mattis(LSM)の定理は、スピンが半整数のときの反強磁性ハイゼンベルグモデルがエネルギーギャップを持たないことを保証してくれる定理です。この定理により、半整数スピンのときのHaldane予想が正しいことを部分的に示すことができます。

1次元系におけるLSM定理の内容を述べます。スピン $S$ が半整数のとき、反強磁性ハイゼンベルグモデルの第一励起エネルギー $E_{\rm 1st}$ と基底エネルギー $E_{\rm GS}$ との差はサイト数 $L$ によって次のように上から抑えられる：

\begin{align}
0 < E_{\rm 1st} - E_{\rm GS} \leq \frac{8\pi^2 S^2}{L}.
\end{align}

この定理から、サイト数 $L$ が無限大でエネルギーギャップが消失することがわかります。定理は今は反強磁性ハイゼンベルグモデルを念頭に置いていますが、より広いタイプのモデルにも当てはまることが知られているようです。

こんな便利な定理があるのなら、整数スピンのときも同じようにギャップがないことを示せるんじゃないかと思うかもしれませんが、LSM定理は整数スピンのときは成り立ちません。この定理の証明はスピンが半整数のときにしか成り立たないようにできているからです。では、実際に証明を見てみることにします。

定理の証明

証明の方針は、「スピンをわずかにひねることでいくらでも小さい励起を作れる」ことを示すというものです。サイト数 $L$ を偶数とすると、Marshall-Leib-Mattisの定理から、基底状態 $\vert\Phi_{\rm GS}\rangle$ は(3)-軸方向⁵ の合計スピンが0です, i.e.,

\begin{align}
{{\hat{S}}_{\rm tot}}^{(3)} \vert\Phi_{\rm GS}\rangle = 0.
\end{align}

ここで $\hat{S}_{\rm tot}^{(3)}$ はすべてのサイトのスピンの(3)-軸方向のスピン演算子の和です。ここから、(3)-軸回りの回転を作る演算子がスピン演算子の指数関数で書けることを思い出すと、基底状態は(3)-軸回りの回転に対して不変（対称）な状態であることがわかります。モデルが反強磁性（スピンをなるべく反対向きに向けたい）かつ、回転対称性があったことから、この帰結は自然に理解できるでしょう。

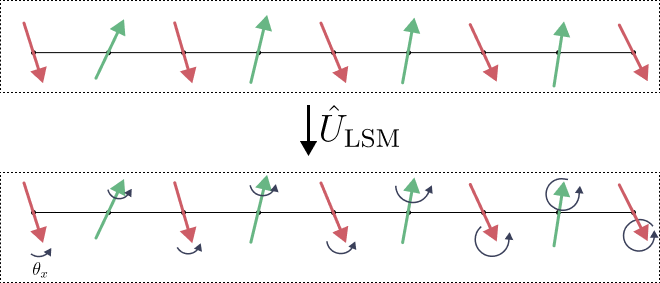
基底状態はすべてのスピンを同じ角度だけ回したときに不変であったので、今度はスピンをわずかに角度を変えながら徐々に傾けていくことを考えます。次のような演算子を考えます。

\begin{align}
\hat{U}_{\rm LSM} &:= \exp[-i\sum_{x=1}^L \theta_x \hat{S}_x^{(3)}]\\
\theta_x &:= \frac{2\pi}{L}x = \Delta\theta x.
\end{align}

この演算子は、位置 $x$ のスピンを角度 $\Delta\theta x$ だけずらしていくはたらきをします。今度は一斉に回すのではなく、隣同士わずかに異なる角度だけずらす状態を作るのです。ちょうど端から端までで1回転させます。この演算子を基底状態に作用させた状態$\vert\Phi_{\rm LSM}\rangle$ を試しに励起状態だとしてエネルギー固有値を計算してみましょう。すると、次の関係を満たすことが計算により確かめられます：

\begin{align}
\langle\Phi_{\rm LSM}\vert \hat{H}\vert\Phi_{\rm LSM}\rangle - E_{\rm GS} \leq \frac{8\pi^2 S^2}{L}.
\end{align}

これは示したい定理にだいぶ近いことを言っているように見えます。一旦この式を示しておきましょう。

次の便利な関係式を用います。

\begin{align}
e^{i\theta\hat{S}^{(3)}} \,\hat{S}^{\pm} \,e^{-i\theta\hat{S}^{(3)}} = e^{\pm i\theta}\,\hat{S}^{\pm}.
\end{align}

ここで、 $\hat{S}^{\pm} := \hat{S}^{(1)} \pm i\hat{S}^{(2)}$ はスピンの昇降演算子です。これを用いると、ハミルトニアンの各項は $\hat{U}_{\rm LSM}$ で次のように変換します。

\begin{align}
\hat{U}^\dagger_{\rm LSM} \, \hat{S}_x\cdot\hat{S}_{x+1} \,\hat{U}_{\rm LSM} 
&= \hat{U}^\dagger_{\rm LSM} \, \left(\frac{1}{2}\left(\hat{S}_x^{+}\hat{S}_{x+1}^- + \hat{S}_x^-\hat{S}_{x+1}^+\right) + \hat{S}_x^{(3)}\hat{S}_{x+1}^{(3)}\right)\,\hat{U}_{\rm LSM} \\
&= \frac{1}{2} \left(e^{i(\theta_x-\theta_{x+1})}\hat{S}_x^{+}\hat{S}_{x+1}^- + e^{-i(\theta_x-\theta_{x+1})}\hat{S}_x^-\hat{S}_{x+1}^+\right) + \hat{S}_x^{(3)}\hat{S}_{x+1}^{(3)}
\end{align}

元々の項との差をとると、

\begin{align}
\hat{U}^\dagger_{\rm LSM} \, \hat{S}_x\cdot\hat{S}_{x+1} \,\hat{U}_{\rm LSM} -\hat{S}_x\cdot\hat{S}_{x+1}
&= \frac{1}{2}\left((e^{-i\Delta\theta}-1)\hat{S}_x^+\hat{S}_{x+1}^- + (e^{i\Delta\theta}-1)\hat{S}_x^-\hat{S}_{x+1}^+\right)
\end{align}

を得ることができます。これを $x$ について和をとったものと、また $\theta_x\to-\theta_x$に置き換えた式は次のようになります。

\begin{align}
\hat{U}^\dagger_{\rm LSM} \, \hat{H} \,\hat{U}_{\rm LSM} - \hat{H}
&= \frac{1}{2}\sum_{x=1}^L \left((e^{-i\Delta\theta}-1)\hat{S}_x^+\hat{S}_{x+1}^- + (e^{i\Delta\theta}-1)\hat{S}_x^-\hat{S}_{x+1}^+ \right)\\
\hat{U}_{\rm LSM} \, \hat{H} \,\hat{U}^\dagger_{\rm LSM} - \hat{H}
&= \frac{1}{2}\sum_{x=1}^L \left((e^{i\Delta\theta}-1)\hat{S}_x^+\hat{S}_{x+1}^- + (e^{-i\Delta\theta}-1)\hat{S}_x^-\hat{S}_{x+1}^+ \right).
\end{align}

以上より、$\vert\Phi_{\rm LSM}\rangle$ でのエネルギー固有値と基底エネルギーの差は次のように上から抑えることができます。

\begin{align}
\langle \Phi_{\rm LSM}\vert\hat{H}\vert\Phi_{\rm LSM}\rangle - E_{\rm GS}
&= \langle\Phi_{\rm GS}\vert(\hat{U}^\dagger_{\rm LSM}\hat{H}\hat{U}_{\rm LSM}- \hat{H})\vert\Phi_{\rm GS}\rangle \\
&\leq \langle\Phi_{\rm GS}\vert(\hat{U}^\dagger_{\rm LSM}\hat{H}\hat{U}_{\rm LSM}- \hat{H})\vert\Phi_{\rm GS}\rangle + \langle\Phi_{\rm GS}\vert(\hat{U}_{\rm LSM}\hat{H}\hat{U}^\dagger_{\rm LSM}- \hat{H})\vert\Phi_{\rm GS}\rangle\\
&= (\cos\Delta\theta - 1) \sum_{x=1}^L\langle\Phi_{\rm GS}\vert\left(\hat{S}_x^+\hat{S}_{x+1}^- + \hat{S}_x^-\hat{S}_{x+1}^+\right)\vert\Phi_{\rm GS}\rangle\\
& \leq  2(1-\cos\Delta\theta)\sum_{x=1}^L\left\vert\langle\Phi_{\rm GS}\vert(\hat{S}_x^{(1)}\hat{S}_{x+1}^{(2)} + \hat{S}_x^{(2)}\hat{S}_{x+1}^{(2)})\vert\Phi_{\rm GS}\rangle\right\vert\\
& \leq (\Delta\theta)^2 2S^2L = \frac{8\pi^2S^2}{L}
\end{align}

ここで、1から2行目では変分原理より正の値と保証されている余分な項を加えており、3から4行目では昇降演算子を成分ごとに書き直し、不等式の向きに注意して1と $\cos\Delta\theta$ の順番を入れ替えています。4から5行目では $\cos x\geq 1-x^2/2$ と、演算子の性質 $\vert\langle\Phi\vert\hat{S}_x^{(\alpha)}\hat{S}_y^{(\alpha)}\,\vert \Phi\rangle\vert\leq S^2$ を用います。これで、目的の式が示されました。

式をみると、これでLSM定理が証明されたようにも見えますが、実はまだやり残したことがあります。先ほどお試しに定義した $\vert\Phi_{\rm LSM}\rangle$ が本当は基底状態と同じなんじゃないの？？という疑いを晴らす必要があります。変換してたまたま基底状態と同じ状態だったら先ほど示した不等式にはなんの意味もありません。嬉しいことに、スピンが半整数のときは $\vert\Phi_{\rm LSM}\rangle$ と $\vert\Phi_{\rm GS}\rangle$ が直交することをきちんと示すことができます。

直交性の証明の鍵となるのは、スピンの大きさに応じて $\langle \Phi_{\rm LSM}\vert\Phi_{\rm GS}\rangle$ を平行移動したときにかかる因子が $\pm1$ で異なることです。つまり、スピンの大きさ $S$ を用いて、この内積は次の関係を満たすことを示せます：

\begin{align}
 \langle \Phi_{\rm LSM}\vert\Phi_{\rm GS}\rangle = (-1)^{2S}\,\langle \Phi_{\rm LSM}\vert\Phi_{\rm GS}\rangle.
\end{align}

ここから、スピンが半整数のときは $\langle \Phi_{\rm LSM}\vert\Phi_{\rm GS}\rangle=0$　となり、$\vert\Phi_{\rm LSM}\rangle $ が基底状態とは別の状態であることが言えます。

スピンの鎖の位置を一つずらす平行移動演算子を次で定義します：

\begin{align}
\hat{T}^\dagger\, \hat{S}_x^{(\alpha)} \,\hat{T} = \hat{S}_{x-1}^{(\alpha)}.
\end{align}

ここで、周期境界条件を用いて $L+1$と$1$、 $L$と$0$を同一視します。基底状態に平行移動を施してもまた基底状態であるので、次の式が成立します。

\begin{align}
\langle \Phi_{\rm GS}\vert\Phi_{\rm LSM}\rangle = \langle\Phi_{\rm GS}\vert\hat{U}_{\rm LSM}\vert\Phi_{\rm GS}\rangle = \langle\Phi_{\rm GS}\vert\hat{T}^\dagger\hat{U}_{\rm LSM}\hat{T}\vert\Phi_{\rm GS}\rangle.
\end{align}

次に $\hat{U}_{\rm LSM}$　に平行移動を施した演算子がどのようなものか計算して確かめます。

\begin{align}
\hat{T}^\dagger\hat{U}_{\rm LSM}\hat{T}
&= \hat{T}^\dagger \exp[-i\sum_{x=1}^L\theta_x\hat{S}_x^{(3)}]\hat{T}\\
&= \exp[-i\sum_{x=0}^{L-1}\theta_x\hat{S}_x^{(3)}]\exp[-i\Delta\theta\sum_{x=0}^{L-1}\hat{S}_x^{(3)}]
\end{align}

2行目において、$\theta_x$ を$x=0$にまで拡張して、 $\theta_0=0$としています。よって、2行目の前半部分は、

\begin{align}
\exp[-i\sum_{x=0}^{L-1}\theta_x\hat{S}_x^{(3)}] = \exp[-i\sum_{x=1}^{L-1}\theta_x\hat{S}_x^{(3)}] = e^{i\theta_L\hat{S}_L^{(3)}}\,\hat{U}_{\rm LSM}
\end{align}

となり、 $\theta_L = 2 \pi$ であるので、角運動量の一般論から、次のことが言えます。

\begin{align}
e^{2\pi i \hat{S}_L^{(3)} } = (-1)^{2S}
\end{align}

以上より、 $\sum_{x=0}^{L-1}\hat{S}_x^{(3)}$ が全スピン演算子で、基底状態に作用すると0になることを考慮すると、

\begin{align}
\langle\Phi_{\rm GS}\vert\Phi_{\rm LSM}\rangle = \langle \Phi_{\rm GS}\vert (-1)^{2S}\hat{U}_{\rm LSM} \exp[-i\Delta\theta \hat{S}_{\rm tot}^{(3)}]\vert\Phi_{\rm GS}\rangle = (-1)^{2S}\langle \Phi_{\rm GS}\vert\Phi_{\rm LSM}\rangle
\end{align}

と、目的の式を示すことができました。

結局、LSM定理の証明において、スピンをわずかにひねった状態が基底状態と直交することを確認する段階で、スピンが整数か半整数かが効いてくることがわかりました。以上によりLSM定理の説明と証明が完了しました。この定理により、スピンが半整数のとき、反強磁性ハイゼンベルグモデルの基底エネルギーにギャップがないことを確かめることができました。

LSM定理について、田崎先生がYouTubeで動画もあげているので興味のある方はこちらもご覧ください。

次に、今度は整数スピン $S=1$ の量子スピン系でHaldane予想の主張に合致する結果を厳密に示すことができる例を紹介します。

AKLTモデル

1987年、Affleck, Kennedy, Lieb, Tasakiらによって提唱されたモデルが今回お話しするAKLTモデルです。このモデルは、スピン $S=1$ の1次元量子系で、基底状態が厳密に書き下せます。また、Haldane予想での整数スピンの系の性質であるエネルギーギャップと、相関関数の指数関数的な減衰が確かめられる例となっています。AKLTモデルはハイゼンベルグモデルとは若干異なるので、この結果は直接Haldane予想の"証明"とはなりません。しかし、Haldane予想を支持する結果であるとともに、その後の研究に大きな影響を与えるものでした。

まず、AKLTモデルの説明をします。そしてAKLTモデルの基底状態、Valence Bond Solid state(VBS状態)、を構築します。実はこの基底状態はテンソルネットワークの文脈で知られる「行列積状態 (Matrix Product States)」であることが知られています。最後に、エネルギーギャップの存在と相関関数の減衰について議論の方針だけ述べようと思います（、計算が多めなので）。

モデルの説明

AKLTモデルはスピン $S=1$ の1次元量子系で、以下のハミルトニアンで表されます。

\begin{align}
\hat{H}_{\rm AKLT} = \sum_{x=1}^L \left[\hat{S}_x\cdot\hat{S}_{x+1} + \frac{1}{3}(\hat{S}_x\cdot\hat{S}_{x+1})^2\right]
\end{align}

これをみると、ハイゼンベルグモデルとの違いが第2項に現れていることがわかります。この項があることにより、基底状態を厳密に書き下せるようになります。そのため、以下の式が成り立つことに注目します。

\begin{align}
\hat{S}_x\cdot\hat{S}_{x+1} + \frac{1}{3}(\hat{S}_x\cdot\hat{S}_{x+1})^2 = 2\hat{P}_2[\hat{S}_x+\hat{S}_{x+1}] - \frac{2}{3}.
\end{align}

ここで、 $\hat{P}_{J}[\hat{J}]$ は $\hat{J}$の固有状態の中で、固有値 $J(J+1)$を持つ空間への射影演算子です。つまり上式の $\hat{P}_2$ は隣り合うスピンの合成スピンが2となる空間に射影する演算子となります。この変形は次の関係式を利用すれば簡単に示されます。

\begin{align}
\hat{S}_x \cdot \hat{S}_{x+1} 
&= \frac{1}{2}\left[(\hat{S}_x+\hat{S}_{x+1})^2 - \hat{S}_x^2 - \hat{S}_{x+1}^2\right]\notag\\
&= \frac{1}{2}\left[2(2+1)\hat{P}_2 + 1(1+1)\hat{P}_1\right]-2\notag\\
&= 3\hat{P}_2 + \hat{P}_1 -2
\end{align}

この式に、この式を2乗して3で割ったものを足せば、目的の式が示されます。よって、AKLTモデルのハミルトニアンは定数の差を除いて以下のハミルトニアンと等しいことがわかります。

\begin{align}
\hat{H}'_{\rm AKLT} = \sum_{x=1}^L \hat{P}_2[\hat{S}_x+\hat{S}_{x+1}]
\end{align}

基底状態を求める

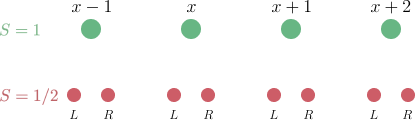
AKLTハミルトニアンは、隣り合うスピン $S=1$ の合成したスピンが2のときだけ正の値を吐くようなものでした。そこで、一番エネルギーの小さい基底状態は「隣り合うスピンの合成スピンが0か1にしかならないようにうまく配置する」ことで作れそうな気がしませんか？それを実現する巧妙？な方法があります。それは、スピン $S=1$ を2つのスピン $S=1/2$ を使って表すというものです。

各サイト $x$ の $S=1$ の基底、

\begin{align}
\vert\psi_x^{-1}\rangle,\quad \vert\psi_x^{0}\rangle, \quad \vert\psi_x^{1}\rangle
\end{align}

を、 $(x,L),(x,R)$ に棲む2つのスピンで次のように表すことができます。

\begin{align}
\vert\psi_x^{-1}\rangle
&= \mathscr{S}(\vert\psi_{x,L}^\downarrow\rangle\vert\psi_{x,R}^\downarrow\rangle)\\
\frac{1}{\sqrt{2}}\vert\psi_x^{0}\rangle
&= \mathscr{S}(\vert\psi_{x,L}^\uparrow\rangle\vert\psi_{x,R}^\downarrow\rangle) = \mathscr{S}(\vert\psi_{x,L}^\downarrow\rangle\vert\psi_{x,R}^\uparrow\rangle)\\
\vert\psi_x^{1}\rangle
&= \mathscr{S}(\vert\psi_{x,L}^\uparrow\rangle\vert\psi_{x,R}^\uparrow\rangle)
\end{align}

ここで $\mathscr{S}$ は対称化演算子で、2つのスピン $1/2$ をきちんとスピン $1$ の空間に対応させる働きをします。具体的には、2つのスピンがシングレット(合成スピンが0)の場合0を返してしまう演算子です。

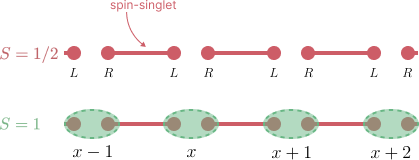
この考え方を使って、次のような状態(pre-VBS状態)を考えます。

\begin{align}
\vert\Phi_{\rm pre-VBS}\rangle = \otimes_{x=1}^L\frac{1}{\sqrt{2}}\left[\vert\psi_{x,R}^\uparrow\rangle\vert\psi_{x+1,L}^\downarrow\rangle - \vert\psi_{x,R}^\downarrow\rangle\vert\psi_{x+1,L}^\uparrow\rangle\right]
\end{align}

これはサイト $2L$ のスピン $1/2$ の鎖で、 $(x,R),(x+1,L)$がシングレット状態を作ってるものです。このようにして状態を作ると、スピン1に直したときに絶対に合成スピンが2にはなりません。なぜなら隣り合うスピン1の合成は、隣り合う4つのスピン $1/2$ の合成であり、そのうち2つがシングレットを作ってしまうと、どう頑張っても合計スピンが2にはならないからです。よって、このpre-VBS状態に対称化演算子を作用させてスピン1の鎖に直した状態：

\begin{align}
\vert\Phi_{\rm VBS}\rangle = (\otimes_{x}\mathscr{S})\vert\Phi_{\rm pre-VBS}\rangle
\end{align}

はAKLTモデルの基底状態になっていると考えられます。VBS状態を図で表すとこのようになります。赤い棒がシングレットで、緑の丸が対称化演算子をかけたものになります。

以上でAKLTモデルの基底状態を表すことができました。⁶

VBS状態の性質

ここまで、AKLTモデルにおける基底状態、VBS状態、を構築してきました。具体的な計算は省略して、VBS状態の性質についてまとめていこうと思います。気になるのは、

基底状態は一意か
エネルギーギャップがあるか
相関関数は指数関数的に減衰するか

です。

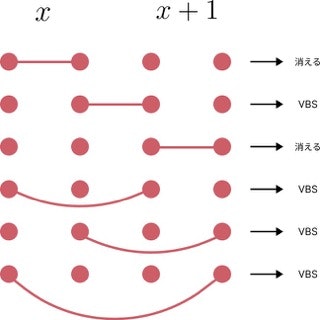
1つ目の基底状態の一意性はほとんど明らかです。スピン $1/2$ の鎖に書き直したとき、各サイト $x$ にシングレットを作るスピンの片方が入っていればそれは基底状態になります。対称化演算子を最後に作用させるので、4つのスピンで可能なシングレットのペアを作ると、すべて消えるかVBS状態になるかの2択となります。

よって、VBS状態以外でエネルギーが0となる基底状態はありえません。

2つ目のエネルギーギャップについては解析的に示すことができます。ハミルトニアンが以下の式を満たせば良いことを証明する必要があります。(演算子が正であるとは、すべての状態ベクトルに関する期待値が正であるということです。）

\begin{align}
\hat{H}_{\rm AKLT}'^2 \geq \varepsilon \hat{H}_{\rm AKLT}'
\end{align}

こちらは腕力で示すことになります。上の式を満たす $\varepsilon$ を見つけてこればよいのです。この性質もきちんと証明されています。

最後の相関関数の減衰については、行列積状態(MPS)を用いて基底状態を表しておくことで比較的簡単に示すことができます。この計算はテンソルネットワークを使った計算のいい練習問題となります。計算結果だけ述べておくと、 $L\to\infty$ で、

\begin{align}
\langle \Phi_{\rm VBS}\vert \hat{S}_x^{(3)}\cdot\hat{S}_{x+r}^{(3)}\vert\Phi_{\rm VBS}\rangle = 4\left(-\frac{1}{3}\right)^r
\end{align}

と、指数関数的に減衰することが確かめられます。

以上、AKLTモデルの諸性質について紹介しました。AKLTモデルが実際に、Haldane予想にあるような整数スピンの系の性質を持ち合わせていることが確認できました。

おわりに

ここまでお付き合いいただきありがとうございます。楽しめてもらってたら幸いです。

ただ1列に並んだスピンたちが単純な相互作用をする、そこにここまで深い物理を見出すことができることは本当に驚異的です。ここでしたお話にはまだまだ続き？があります。聞いたことがある人も多いとは思いますが、Symmetry protected topological phase (SPT相）は今回紹介したHaldane予想やAKLTモデルにも深く関わっています。他にも量子スピン系は現代物理の各分野につながりがあるように思えます。

知らないことだらけで、まだまだ人生が楽しめそうですね。

茶番：フィギュアスケートで検証

角運動量といえば回転、回転といえばスケート⁷。Haldane予想を $L$ 人のフィギュアスケーターを採用して検証してみます。

まず、スケーターには1列に並んでもらいます。そしてタイミングを合わせてみんなでトリプルアクセル／トリプルループを飛んでもらいます。その際、となり合うスケーター同士の回転の角運動量の内積をとり、その合計を得点とします。Haldane予想が主張するのは、この場合トリプルアクセルを飛べば最低得点と次最低得点の差は $L$ が無限大で0になるが、トリプルループの場合はその差を0にはできないということでした。

果たして、この実験でHaldane予想を検証できるのでしょうか。

答えは否

問題点を列挙します。

まず、量子系のフィギュアスケーターは現実的に用意できない。本編で議論してきた内容は量子力学の効果が正面から効いてきます。
回転をするジャンプが持つ角運動量は軌道角運動量で、本編で議論しているスピン角運動量とは性質が若干ことなる。軌道角運動量の場合そもそも半整数スピンにならない。
反強磁性ハイゼンベルグモデルの基底状態は、スピンを古典近似すればたぶんお互いに反対方向を向くスピンが交互にならぶ状態となる。フィギュアスケーターで、逆回転のジャンプをできる者はそう多くはない。半々には用意できない。
怪我をしそう。

他にもいろいろ問題点がありそうです。実験が大好きな物理学科の民にもこの実験はおすすめしません。

フィギュアスケートにおいて、アクセルは前を向いた状態で踏み切る、ループは後ろ向きで踏み切るジャンプを表す用語です。（こんな適当な説明をしていたら怒られそうですが。）結果として、アクセルジャンプは回転が半整数になり、ループやその他のジャンプは回転が整数になります。 ↩
量子スピン系の場合は古典の場合と違って単に上下に向いたスピンを交互にとった状態, Neel状態, は固有状態になりません。 ↩
整数スピンの場合のスピン相関関数の減衰はOrnstein–Zernike型になります。これは古典系の無秩序相での相関関数の振る舞いと同じです。 ↩
Haldane"予想"と呼ばれてはいますが、主張の根拠はちゃんとあります。 $S=1$ の反強磁性ハイゼンベルグについては数値的にも実験的にも（！）性質が確かめられています。現実に1次元の量子系があるわけではありませんが、3次元空間でもある特定の方向の相互作用だけが強い擬1次元系を用いて実験的に検証することができます。しかし、厳密に・解析的にギャップを示せてはいないようです。 ↩
この記事では座標軸を通常の $x,y,z$ ではなく、 (1), (2), (3)-軸と呼ぶことにします。 ↩
ちゃんとスピン1の基底で書き下して欲しいと思った人もいるかもしれません。スピン1の基底で書くと、行列積状態が自然に現れます。詳しくはTasaki, "Physics and Mathematics of Quantum Mady-Body Systems"を見てください。 ↩
書いていて思ったのですが、スピンといったらスケートでは回転するジャンプではなく、片脚を軸にくるくる回る「スピン」がまず出てきますね。 ↩

【Haldane予想】アクセルとループは何が違う？