Winograd 畳み込みアルゴリズムをTVMで実装する その2

前回の記事では、Winograd アルゴリズムの概要、TVM によるアルゴリズムの定義、ナイーブな GPU 実装、までを説明しました。今回は、ナイーブなスケジュールから出発して、ステップバイステップでスケジュールを改善していきます。最終的には、 TVM 本家の Direct Convolution よりも 2 倍近く速くなります。また、TVM には AMDGPU 向けのバックエンドもあるので、AMDGPU 用のカーネルを生成することもできます。NVIDIA GPU 向けに高速化したスケジュールが、 AMDGPU でも高速に動作することを最後に示します。

高速化

1. 入力変換、出力逆変換の改善

まずは、入力タイルの変換 $V$ の計算スケジュールを改善します。$V$ は、サイズ (4, 4, 全タイル数, チャネル数) で、入力タイル $d$ に変換行列 $B^T$ を左右からかけた変換 $B^T d B$ を全タイル数・チャネル数分束ねた配列でした。最初に実装したスケジュールでは、$V$ の各 (4, 4, 全タイル数, チャネル数) の値を、一つのスレッドに計算させました。つまり、一つの 4 x 4 タイルの変換 $B^T d B$ に 16 個 のスレッドを使っていました。この計算に必要なのは 4 x 4 の入力タイル $d$ のみです。16個のスレッドは同じ 4 x 4 の入力 $d$ にグローバルメモリを通して何度もアクセスしていることになり、非効率です。

そこで、一つのスレッドで 4 x 4 の 1 タイルの変換をするように変更します。4 x 4 の値を計算する中で何度も同じ入力 $d$ にアクセスしないように、一度 $d$ をグローバルメモリからスレッド内のレジスタにキャッシュしておく必要があります。また、4 x 4 の出力の途中結果を保持しておくためのレジスタも用意します。

TVM でレジスタをグローバルメモリへのキャッシュとして使うには、Schedule.cache_read(..., "local") という API を使うのですが、コードでは $d$ はメモリというよりも"入力画像をタイル状に並び替える" という計算そのものです(前回の記事中、TVM による $d$ の定義を参照)。そこで、ここでは

s[d].compute_at(s[V], ...)

という API を使いました。これにより、$V$ を計算するスレッドが必要とする入力 $d$ を、必要な分だけレジスタにキャッシュする、ということが実現されます。

途中結果を保持するレジスタを宣言するには、Schedule.cache_write(..., "local") という API を使います。cache_write(...), cache_read(...) を使うには、対応する compute_at(...) が必要です。compute_at(...) によって、スレッド内のどのループでキャッシュへの読み書きをするのか指定します。

以上を踏まえて、改善した入力変換 $V$ のスケジュールは以下のように記述します。

VL = s.cache_write(V, "local")
eps, nu, p, c = s[V].op.axis
s[V].reorder(p, c, eps, nu) # 4 x 4 のループを内側に持ってくることで、各スレッドが 4 x 4 の値を計算するようになる
po, pi = s[V].split(p, factor=num_thread)
co, ci = s[V].split(c, factor=num_thread)
s[V].bind(pi, tvm.thread_axis("threadIdx.y"))
s[V].bind(ci, tvm.thread_axis("threadIdx.x"))
s[V].bind(po, tvm.thread_axis("blockIdx.y"))
s[V].bind(co, tvm.thread_axis("blockIdx.x"))
s[VL].compute_at(s[V], ci)
s[d].compute_at(s[V], ci)

tvm.lower(schedule, [...], simple_mode=True) という API を使うと、TVM が上記のスケジュールをどのような中間表現 (Intermediate Representation, 以下 IR) に変換しているか調べることができます。IR をダンプしてみると、以下のようになっていました。

produce V {
  // attr [iter_var(blockIdx.y, , blockIdx.y)] thread_extent = 4
  // attr [d] storage_scope = "local"
  allocate d[float32 * 1 * 1 * 4 * 4]
  // attr [V.local] storage_scope = "local"
  allocate V.local[float32 * 4 * 4 * 1 * 1]
  // attr [iter_var(threadIdx.y, , threadIdx.y)] thread_extent = 16
  // attr [iter_var(blockIdx.x, , blockIdx.x)] thread_extent = 784
  // attr [iter_var(threadIdx.x, , threadIdx.x)] thread_extent = 16
  produce d {
    unrolled (eps, 0, 4) {
      unrolled (nu, 0, 4) {
        d[((eps*4) + nu)] = tvm_if_then_else((((((1 - eps) <= ((((blockIdx.x*16) + threadIdx.x)/112)*2)) && (((((blockIdx.x*16) + threadIdx.x)/112)*2) < (225 - eps))) && ((1 - nu) <= ((((blockIdx.x*16) + threadIdx.x) % 112)*2))) && (((((blockIdx.x*16) + threadIdx.x) % 112)*2) < (225 - nu))), A[(((((((((blockIdx.y*16) + threadIdx.y)*112) + (((blockIdx.x*16) + threadIdx.x)/112))*224) + ((eps*112) + (((blockIdx.x*16) + threadIdx.x) % 112)))*2) + nu) + -225)], 0.000000f)
      }
    }
  }
  produce V.local {
    unrolled (eps.c, 0, 4) {
      unrolled (nu.c, 0, 4) {
        V.local[((eps.c*4) + nu.c)] = 0.000000f
        unrolled (r_eps, 0, 4) {
          unrolled (r_nu, 0, 4) {
            V.local[((eps.c*4) + nu.c)] = (V.local[((eps.c*4) + nu.c)] + ((d[((r_eps*4) + r_nu)]*select(((r_eps == 3) && (eps.c == 3)), -1.000000f, select((((r_eps == 3) && (eps.c == 2)) || (((r_eps == 3) && (eps.c == 1)) || (((r_eps == 3) && (eps.c == 0)) || ((r_eps == 2) && (eps.c == 3))))), 0.000000f, select((((r_eps == 2) && (eps.c == 2)) || ((r_eps == 2) && (eps.c == 1))), 1.000000f, select(((r_eps == 2) && (eps.c == 0)), -1.000000f, select(((r_eps == 1) && (eps.c == 3)), 1.000000f, select(((r_eps == 1) && (eps.c == 2)), -1.000000f, select((((r_eps == 1) && (eps.c == 1)) || !(((r_eps == 1) && (eps.c == 0)) || (((r_eps == 0) && (eps.c == 3)) || (((r_eps == 0) && (eps.c == 2)) || (((r_eps == 0) && (eps.c == 1)) || !((r_eps == 0) && (eps.c == 0))))))), 1.000000f, 0.000000f))))))))*select(((r_nu == 3) && (nu.c == 3)), -1.000000f, select((((r_nu == 3) && (nu.c == 2)) || (((r_nu == 3) && (nu.c == 1)) || (((r_nu == 3) && (nu.c == 0)) || ((r_nu == 2) && (nu.c == 3))))), 0.000000f, select((((r_nu == 2) && (nu.c == 2)) || ((r_nu == 2) && (nu.c == 1))), 1.000000f, select(((r_nu == 2) && (nu.c == 0)), -1.000000f, select(((r_nu == 1) && (nu.c == 3)), 1.000000f, select(((r_nu == 1) && (nu.c == 2)), -1.000000f, select((((r_nu == 1) && (nu.c == 1)) || !(((r_nu == 1) && (nu.c == 0)) || (((r_nu == 0) && (nu.c == 3)) || (((r_nu == 0) && (nu.c == 2)) || (((r_nu == 0) && (nu.c == 1)) || !((r_nu == 0) && (nu.c == 0))))))), 1.000000f, 0.000000f)))))))))
          }
        }
      }
    }
  }
  unrolled (eps, 0, 4) {
    unrolled (nu, 0, 4) {
      V[((((((((blockIdx.y*16) + threadIdx.y)*784) + blockIdx.x)*16) + threadIdx.x) + (eps*3211264)) + (nu*802816))] = V.local[((eps*4) + nu)]
    }
  }
}

意図した通りになっていそうですね。出力の逆変換も上記と同様に、一つのスレッドで 2 x 2 の出力を計算するように変更します。詳細は似ているので省きます。

ここまでの改善を含めたブランチで実行時間を測ってみると、

$ python wino_test.py
Winograd: 18.771 msec, Reference: 2.066 msec

ナイーブな実装の 23.614 ミリ秒から少し高速化することができました。

2. 共有メモリの利用

次に、4 x 4 個分の行列積 $M$ の計算の高速化をします。ここまでのコードをプロファイラにかけると、95% の実行時間がこの計算に費やされていました。そのため、高速化の余地が大いにあります。

行列積は、GPU プログラミングの入門でもよく取り上げられるように、GPU により高い性能を出しやすい問題です。高速化の手段としては、共有メモリの利用がまず挙げられます。現在のスケジュールでは、出力行列の各要素を1スレッドで計算していますが、同じ行・列のスレッドは入力行列の同じ要素にアクセスします。そのため、同じグローバルメモリに何度もアクセスしていることになり、大変非効率です。そこで、スレッドブロックごとにメモリの再利用を高めるために、共有メモリの利用を考えます。共有メモリを使った行列積では、以下のように行列積をブロック分割し、ブロックごとの積和を計算します。ブロック内では、同じ行・列のスレッドは共有メモリの同じ要素にアクセスするようになり、メモリ効率が高まります。

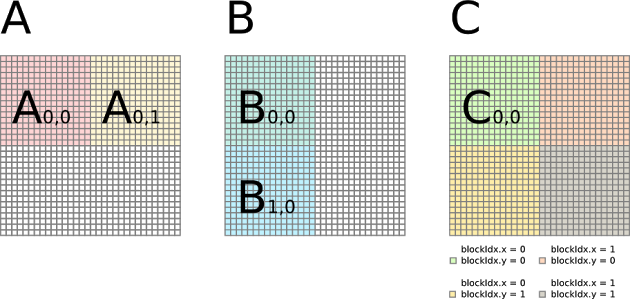
(画像元: http://www.es.ele.tue.nl/~mwijtvliet/5KK73/?page=mmcuda)

TVM で共有メモリを使うには、Schedule.cache_read(..., "shared") という API を使います。行列 $U$ と $V$ の共有メモリを、以下のように宣言します。共有メモリのサイズを明示的に指定することはできません。サイズは、共有メモリへのアクセスパターンから TVM が適切な値を決定します。

UU = s.cache_read(U, 'shared', [M])
VV = s.cache_read(V, "shared", [M])

スレッドブロックの設定に変更はありません。4 x 4 個の行列積はそれぞれ別のスレッドブロックで計算します。

ML = s.cache_write(M, "local")
eps, nu, k, p = s[M].op.axis
ko, ki = s[M].split(k, factor=num_thread)
po, pi = s[M].split(p, factor=num_thread)
z = s[M].fuse(eps, nu)
s[M].bind(ki, tvm.thread_axis("threadIdx.y"))
s[M].bind(pi, tvm.thread_axis("threadIdx.x"))
s[M].bind(ko, tvm.thread_axis("blockIdx.y"))
s[M].bind(po, tvm.thread_axis("blockIdx.x"))
s[M].bind(z, tvm.thread_axis("blockIdx.z"))
s[ML].compute_at(s[M], pi)

次に、行列積をブロック分割します。内積をとる次元 reduce_axis を、ブロックのサイズで 2つのループに分割します。

k = s[ML].op.reduce_axis[0]
ko, ki = s[ML].split(k, factor=num_thread)

ループ ki の内では共有メモリから値を読んで積和を計算したいので、グローバルメモリから共有メモリへのロードはループ ko で行います。compute_at(..., ko) によってそう指定することができます。

s[UU].compute_at(s[ML], ko)

最後に、共有メモリへのロードを 16 x 16 のスレッドでどのように行うかを指定します。今回のようにそれぞれのスレッドが 1つの値をロードする場合は、以下のように記述します。

yi, xi, ci, ni = s[UU].op.axis
ty, ci = s[UU].split(ci, nparts=num_thread)
tx, ni = s[UU].split(ni, nparts=num_thread)
s[UU].bind(ty, tvm.thread_axis("threadIdx.y"))
s[UU].bind(tx, tvm.thread_axis("threadIdx.x"))

VV についても同様です。

__syncthreads() のようなスレッド同期 API は TVM にはありません。ユーザーはスレッドの同期を気にする必要はなく、TVM が適切な箇所に同期命令を挿入します。

このスケジュールから TVM がどのような IR をつくるか見てみましょう。

produce M {
  // attr [iter_var(blockIdx.z, , blockIdx.z)] thread_extent = 16
  // attr [M.local] storage_scope = "local"
  allocate M.local[float32 * 1 * 1 * 1 * 1]
  // attr [U.shared] storage_scope = "shared"
  allocate U.shared[float32 * 1 * 1 * 16 * 16]
  // attr [V.shared] storage_scope = "shared"
  allocate V.shared[float32 * 1 * 1 * 16 * 16]
  // attr [iter_var(blockIdx.y, , blockIdx.y)] thread_extent = 4
  // attr [iter_var(threadIdx.y, , threadIdx.y)] thread_extent = 16
  // attr [iter_var(blockIdx.x, , blockIdx.x)] thread_extent = 784
  // attr [iter_var(threadIdx.x, , threadIdx.x)] thread_extent = 16
  produce M.local {
    M.local[0] = 0.000000f
    unrolled (c.outer, 0, 4) {
      produce U.shared {
        // attr [iter_var(threadIdx.y, , threadIdx.y)] thread_extent = 16
        // attr [iter_var(threadIdx.x, , threadIdx.x)] thread_extent = 16
        U.shared[((threadIdx.y*16) + threadIdx.x)] = U[(((((((blockIdx.z*4) + blockIdx.y)*64) + c.outer) + (threadIdx.y*4))*16) + threadIdx.x)]
      }
      produce V.shared {
        // attr [iter_var(threadIdx.y, , threadIdx.y)] thread_extent = 16
        // attr [iter_var(threadIdx.x, , threadIdx.x)] thread_extent = 16
        V.shared[((threadIdx.y*16) + threadIdx.x)] = V[(((((((blockIdx.z*784) + blockIdx.x)*64) + c.outer) + (threadIdx.y*4))*16) + threadIdx.x)]
      }
      unrolled (c.inner, 0, 16) {
        M.local[0] = (M.local[0] + (U.shared[((threadIdx.y*16) + c.inner)]*V.shared[((threadIdx.x*16) + c.inner)]))
      }
    }
  }
  M[((((((((blockIdx.z*4) + blockIdx.y)*16) + threadIdx.y)*784) + blockIdx.x)*16) + threadIdx.x)] = M.local[0]
}

$U$, $V$ それぞれに 16 x 16 の共有メモリが割り当てられ、 分割したブロックごとに共有メモリへのロードが行われていること、最内ループでは共有メモリにのみアクセスしていることが確認できます。

共有メモリを導入したブランチで、実行時間を測ってみます。

$ python wino_test.py
Winograd: 4.225895 msec, Reference: 2.066044 msec

18.7 ミリ秒から 4.2 ミリ秒と、共有メモリを使っていなかった場合と比べて大きく高速化されました。

3. バンクコンフリクトをなくす

ここまでのコードをプロファイラにかけると、共有メモリのバンド幅がボトルネックになっていることと、共有メモリロード時のバンクコンフリクトが大量に起こっていることが分かりました。

共有メモリのバンクコンフリクトは、一つのメモリーバンクに同一ワープから複数のアクセスが起こると発生します。先ほどの共有メモリを導入したスケジュールの IR の最内ループに相当する部分、

unrolled (c.inner, 0, 16) {
        M.local[0] = (M.local[0] + (U.shared[((threadIdx.y*16) + c.inner)]*V.shared[((threadIdx.x*16) + c.inner)]))
      }

を見てみると、V.shared[((threadIdx.x*16) + c.inner)] の部分が怪しそうです。このアクセスパターンだと、となり合うスレッドはストライド 16 で V.shared にアクセスします。メモリーバンクの数が16か32の場合、バンクコンフリクトが発生します。アクセスパターンを改善するには、配列 $V$ のレイアウトを転置するだけでよさそうです。

V のレイアウトを転置して、実行時間を測ってみます。コードはこちら。

$ python wino_test.py
Winograd: 2.591631 msec, Reference: 2.163305 msec

メモリのレイアウトを変えるだけで、4.2 ミリ秒から　2.59 ミリ秒に高速化されました。

もう一度プロファイラをかけると、バンクコンフリクトが完全になくなっていることが確認できました。

4. より良い行列積スケジュールの利用

ここまで見てきたとおり、行列積の高速化を続けていけば、さらなる Winograd アルゴリズムの高速化が期待できそうです。ですが、行列積の高速化には終わりがなく、続けていくのは大変です。幸運なことに、行列積はよく性能評価にも使われるので、TVM にもすでに良い実装があります。そこで、今回は TVM 公式サイト上のあるチュートリアル で実装されているスケジュールを利用しました。このスケジュールにわずかな変更を加え、

schedule_batched_sgemm(s, U, V, M)

と使えるようにしました。スケジュールの詳しい解説は上記チュートリアルでされているのでここでは省きますが、主なポイントとして、

• 8 x 8 のスレッドブロックで、64 x 64 の出力を計算する
• 64 x 8 の共有メモリを使う。共有メモリのロードはベクトル化する。
• メモリアクセスの再利用をさらに高めるために、 8 つのレジスタを共有メモリのキャッシュとして使う

が挙げられます。また、このスケジュールをそのまま今回の Winograd アルゴリズムの実装に使おうとすると、行列 $U$ の共有メモリへのベクターロードができていませんでした。この問題は、配列 $U$ のレイアウトを、

U = tvm.placeholder((4, 4, num_filter, in_channel), name='U')

から

U = tvm.placeholder((4, 4, in_channel, num_filter), name='U')

にすることで解決しました。

以上の変更を加えたブランチ で実行時間を測ると、

$ python wino_test.py
Winograd: 1.249893 msec, Reference: 2.124259 msec

と、さらに 2倍ほど高速化され、TVM 本家の Direct Convolution にも大きく差をつけることができました。

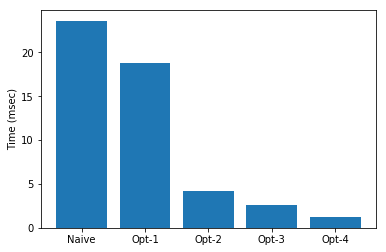
結果

今回実装した各スケジュールのパフォーマンスをまとめます。

最初に実装したナイーブなスケジュールから、20倍近く高速化できました。

また、TVM のコンパイル時のターゲットを CUDA から ROCM にすることで、AMDGPU用のコードを生成することもできます。GTX 1070 Ti と、Radeon R9 Nano 上で、様々な入力に対する Winograd アルゴリズムのパフォーマンスを比較しました。

それぞれのカードの理論性能は、
- GTX 1070 Ti: ベースクロック 7816 GFLOPS, Boost クロック 8186 (wiki リンク)
- R9 Nano: 8192 GFLOPS (wiki リンク)

となっています。ほぼ同等か、わずかに R9 Nano のほうが上、と言えると思います。また、R9 Nano のメモリバンド幅も GTX 1070 Ti のそれを大きく上回ります。そのため、R9 Nano のほうがより良いパフォーマンスを出す、と期待したいところです。

結果は、以下のようになりました。

(N, C, size, K)	GTX 1070 ti	R9 Nano
(1, 64, 224, 64)	1.250	1.234
(1, 128, 122, 128)	1.573	1.173
(1, 128, 128, 128)	0.994	1.138
(1, 64, 56, 64)	0.181	0.136
(1, 64, 64, 32)	0.114	0.163
(1, 64, 112, 128)	0.815	0.650

(単位は全てミリ秒)

概ねどっこいどっこい、といったところでしょうか。少なくとも、AMDGPU でも NVIDIA GPU と同程度の性能を出すことはできる、と言えると思います。今回実装したスケジュールでは、スレッドブロックの幅が 8 か 16 であるため、画像のサイズが 8 で割り切れない場合、 TVM はメモリアクセスのある箇所すべてにインデックスの範囲チェックを挿入していました。これが NVIDIA GPU ではパフォーマンスに大きな悪影響を及ぼしているようで、ほとんど同じ入力サイズにもかかわらず、サイズが 122 の場合は 128 の場合と比べて遥かに遅い、という結果になりました。面白いのは、同じ点が AMDGPU には当てはまらない、ということです。結果の通り、AMDGPU の場合は入力のサイズが 8 で割り切れるかどうかにかかわらず、パフォーマンスはほぼ同じです。AMDGPU は if 文による分岐に対してパフォーマンスが落ちにくい、ということでしょうか。

終わりに

Winograd アルゴリズムの実装・高速化を通して、TVM の使用例を紹介しました。TVM 界隈では、現在 AutoTVM という、スケジュールの高速化を自動化する、という仕組みのオープンソース化が進行中です。これによって、高速な GPU カーネルを書くのがますます簡単になりそうです。最近は様々な Deep Learning フレームワークでバックエンドコンパイラ開発が流行っていますが、その中でも TVM は最も将来性があると思います。今回の記事を通して、TVM に興味を持つ人が増えてくれれば幸いです。

リポジトリへのリンク