なぜやった?
業務で LLM を使った類似文章検索システムの構築を手伝っているが、精度を評価する方法がわからなかったので調べてみました。
類似文章の検索は主に以下のステップで行っています。
- LLM で文章をベクトル化
- ベクトルを使ってコサイン類似度を計算
- コサイン類似度が高い上位 n 件を候補とする
人が感じる2つの文章の類似の度合いと、コサイン類似度がどれくらいマッチしているのかを定量的に表現することを目指しています。
結論から先に言うと
今回は良い結果が得られませんでしたので、この記事はあまり参考にならないと思います。
なので、今回は備忘録として実験結果を記録しておきます。
手法や計算が間違っているかもしれませんので、今後の課題とします。
どうやった?
Yahoo! JAPAN が日本語ベンチマーク用のデータセット JGLUE を公開していて、その中に文ペアの類似度をまとめた JSTS データセットがありますので、そちらを基準として使用します(JSTS データセットは類似度を 0.0 ~ 5.0 の範囲で人が判定したものです)。
計算方法
以下の方法で計算した結果を比較しました。
- BERTscore の F1 値
- BERT でベクトル化して cos 類似度を計算
a. [CLS] トークンのベクトルを使った場合
b. 全トークンの平均ベクトルを使った場合 - SenteceBERT でベクトル化して cos 類似度を計算
a. 2.と同じモデルを使った場合
b. 日本語用 Sentence-BERT モデルを使った場合
評価方法
各計算方法で数値の意味が違うので単純に計算結果を比較するのではなく相関関係を見ます。
今回は、Pearson、Sperman、Kendall 相関係数を使って、上の方法で計算した結果が JSTS データセットの値をどれくらい再現できているかを見てみます。
環境
ライブラリ
- Python: 3.10.12
- Pytorch: 2.0.1
- sentence-transformers: 2.2.2
- transformers: 4.31.0
- scipy: 1.11.2
モデル
haggingface で公開されている以下のモデルを使用しました
- 計算方法 2-a,b と 3-a :
cl-tohoku/bert-base-japanese-whole-word-masking - 計算方法 3-b :
sonoisa/sentence-bert-base-ja-mean-tokens-v2
準備
JSTS データセットをダウンロード
Github で公開されているのでそちらからダウンロードします。
データセットを作成
DataFrame で読み込む
import pandas as pd
df = pd.read_json('JGLUE/datasets/jsts-v1.1/valid-v1.1.json', lines=True)
df.head()
サンプルを抽出
今回は、label を 0.5 刻みで分割してその中から1件ずつデータを取ります。
後で比較しやすいように label は 0.0 ~ 1.0 の範囲に変換します。
import numpy as np
df_sample = df[df['label']==0.0].sample()
for i in np.arange(0.0, 5.0, 0.5):
if i==0.0:
df_sample = pd.concat([df_sample, df.query(f'{i} < label < {i+0.5}').sample()])
else:
df_sample = pd.concat([df_sample, df.query(f'{i} <= label < {i+0.5}').sample()])
df_sample = pd.concat([df_sample, df[df['label']==5.0].sample()])
# まったく同じ文章のペアのものも入れておく
df_sample = pd.concat([df_sample, df[(df['sentence1']==df['sentence2']) & (df['label']==5.0)].sample()])
df_sample.drop(['sentence_pair_id', 'yjcaptions_id'], axis=1, inplace=True)
df_sample.reset_index(drop=True, inplace=True)
# 比較しやすいように label を [0, 1] の区間に変換する
df_sample['label'] = df_sample['label'].apply(lambda x: x/5.0)
df_sample
Dataset を作成
今後の拡張を考えて Dataset を作成しておきます
from datasets import Dataset, DatasetDict
ds = DatasetDict({
"valid": Dataset.from_pandas(df_sample.reset_index(drop=True)),
})
類似度を計算する
BERTscore
各文章に含まれるトークン(単語)で cos 類似度を計算して、それらを基に Precision, Recall, F1 を計算する方法で、2 つの文書間の類似度をはかる指標。
参考:
from bert_score import score
MODEL_NAME = 'cl-tohoku/bert-base-japanese-whole-word-masking'
precisions, recalls, f1s = score(
ds['valid']['sentence1'],
ds['valid']['sentence2'],
model_type=MODEL_NAME,
num_layers=3
)
df_sample['F1_BERTscore'] = f1s.numpy().tolist()
BERT でベクトル化して cos 類似度を計算
以下の記事を参考にさせてもらいました。
参考:
ベクトル化については、 [CLS] トークンのベクトルを使用する方法と全トークンの平均ベクトルを使用する方法を比べてみます。
import torch
import numpy as np
from transformers import BertJapaneseTokenizer, BertModel
from sentence_transformers import SentenceTransformer
from sentence_transformers import models
tokenizer = BertJapaneseTokenizer.from_pretrained(MODEL_NAME)
model = BertModel.from_pretrained(MODEL_NAME)
def sentence_to_vector(sentence, use_cls=True):
# 文を単語に区切って数字にラベル化
tokens = tokenizer(sentence)["input_ids"]
# BERTモデルの処理のためtensor型に変換
input = torch.tensor(tokens).reshape(1,-1)
# BERTモデルに入力し文のベクトルを取得
with torch.no_grad():
outputs = model(input)
if use_cls: # [CLS]トークンのベクトル
vec = outputs.pooler_output[0]
else: # 全トークンのベクトルの平均
last_hidden_state = outputs.last_hidden_state[0]
vec = last_hidden_state.sum(dim=0) / len(last_hidden_state)
return vec
def calc_similarity(data, use_cls=True):
sentence_vector1 = sentence_to_vector(data['sentence1'], use_cls=use_cls)
sentence_vector2 = sentence_to_vector(data['sentence2'], use_cls=use_cls)
return torch.nn.functional.cosine_similarity(sentence_vector1, sentence_vector2, dim=0).detach().numpy().copy()
cos_bert_cls = [calc_similarity(data) for data in ds['valid']]
cos_bert_avg = [calc_similarity(data, use_cls=False) for data in ds['valid']]
df_sample['cos_bert (CLS)'] = cos_bert_cls
df_sample['cos_bert (AVG)'] = cos_bert_avg
SentenceBERT でベクトル化して cos 類似度を計算
SentenceBERT の詳細は以下の記事に詳しく紹介されていますので、そちらを見て頂いた方が正確だと思います。
参考:
大雑把に構成を言うと、
- BERT を使ってトークン毎のベクトルを計算
- pooling 層を通して1つの文章に対応する1つのベクトルにまとめる
pooling の仕方は幾つかあるようですが、今回は上の記事に従って平均をとるようにしました。
クラスの定義
from transformers import BertJapaneseTokenizer, BertModel
import torch
class SentenceBertJapanese:
def __init__(self, model_name_or_path, device=None):
self.tokenizer = BertJapaneseTokenizer.from_pretrained(model_name_or_path)
self.model = BertModel.from_pretrained(model_name_or_path)
self.model.eval()
if device is None:
device = "cuda" if torch.cuda.is_available() else "cpu"
self.device = torch.device(device)
self.model.to(device)
def _mean_pooling(self, model_output, attention_mask):
token_embeddings = model_output[0] #First element of model_output contains all token embeddings
input_mask_expanded = attention_mask.unsqueeze(-1).expand(token_embeddings.size()).float()
return torch.sum(token_embeddings * input_mask_expanded, 1) / torch.clamp(input_mask_expanded.sum(1), min=1e-9)
@torch.no_grad()
def encode(self, sentences, batch_size=8):
all_embeddings = []
iterator = range(0, len(sentences), batch_size)
for batch_idx in iterator:
batch = sentences[batch_idx:batch_idx + batch_size]
encoded_input = self.tokenizer.batch_encode_plus(batch, padding="longest",
truncation=True, return_tensors="pt").to(self.device)
model_output = self.model(**encoded_input)
sentence_embeddings = self._mean_pooling(model_output, encoded_input["attention_mask"]).to('cpu')
all_embeddings.extend(sentence_embeddings)
return torch.stack(all_embeddings)
ベクトル化
model = SentenceBertJapanese(MODEL_NAME)
# トークン数を揃える
max_len = max([len(s) for s in ds['valid']['sentence1']+ds['valid']['sentence2']])
sentences1 = [s.ljust(max_len) for s in ds['valid']['sentence1']]
sentences2 = [s.ljust(max_len) for s in ds['valid']['sentence2']]
s1_vecs = model.encode(sentences1)
s2_vecs = model.encode(sentences2)
df_sample['cos_sbert'] = [torch.nn.functional.cosine_similarity(v1, v2, dim=0).detach().numpy().copy() for v1, v2 in zip(s1_vecs, s2_vecs)]
日本語用 Sentence-BERT モデルを使った場合
cl-tohoku/bert-base-japanese-whole-word-masking を事前学習済みモデルとして改良された日本語用 Sentence-BERT モデルを使用します。
参考:
model_sbert = SentenceBertJapanese("sonoisa/sentence-bert-base-ja-mean-tokens-v2")
s1_vecs = model_sbert.encode(sentences1)
s2_vecs = model_sbert.encode(sentences2)
df_sample['cos_sbert(fine-tuned)'] = [torch.nn.functional.cosine_similarity(v1, v2, dim=0).detach().numpy().copy() for v1, v2 in zip(s1_vecs, s2_vecs)]
計算結果
サンプルデータ
各文ペアは以下の通り
| id | sentence1 | sentence2 |
|---|---|---|
| 0 | 工事中の通りには注意喚起のコーンや誘導版が設置されていました。 | 制服を着た女性が馬に乗ってパレードをしています。 |
| 1 | おしゃれなデザインの建物の前に数台の車が止まり、その手前にはストップの標識があります。 | ふるいデザインの建物の後ろにロバがいて、その後ろには人がいます。 |
| 2 | 草原の上に羊の群れが出来ています。 | 建物の前の広いグリーンに白い動物が何頭もいます。 |
| 3 | 男性が部屋の中でなにかをかまえています。 | 黄色いシャツの男の人が立っています。 |
| 4 | 長机で数人の男女がノートパソコンを操作しています。 | パソコンが一列に並んでいる席にバナナとオレンジを置かれている。 |
| 5 | スケートボードでアクションを起こしている人物の、足元のアップです。 | スケートボードの上に人が乗っている。 |
| 6 | 駅に電車が停まっているところです。 | 駅のホームに止まっている電車のドアに人がいます。 |
| 7 | 白い壁の部屋にソファーとテーブルが置いてあります。 | 部屋の中央にテーブルがあり、手前と奥にソファーがあります。 |
| 8 | 草原にあるベンチの奥にはたくさんの山々が見えます。 | 山が見える平原にベンチがあります。 |
| 9 | テーブルの上に花が生けられた瓶が置いてあります。 | テーブルの上の花瓶に花が生けてあります。 |
| 10 | 椅子に座った子供が手づかみで、食事をしています。 | 椅子に座った子供が、手づかみで食事をしています。 |
| 11 | 道路に黄色いバイクが停められています。 | 黄色いバイクが道路に停めてあります。 |
| 12 | テニスラケットを手にした男女が微笑んでいます。 | テニスラケットを手にした男女が微笑んでいます。 |
計算結果
- label はベンチマークデータセットに入っている値
- F1_BERTscore 以降が今回計算した数値
- いずれも大体下に行くほど数値が大きく(類似度が高く)なっている
- 幾つか大小が前後している部分もある
- cos_sbert(fine-tuned) 以外は非類似の表現が乏しい
| id | label | F1_BERTscore | cos_bert (CLS) |
cos_bert (AVG) |
cos_sbert | cos_sbert (fine-tuned) |
|---|---|---|---|---|---|---|
| 0 | 0.00 | 0.556557 | 0.7383176 | 0.8407013 | 0.8407013 | 0.023326123 |
| 1 | 0.08 | 0.669273 | 0.90153575 | 0.93385535 | 0.9338553 | 0.15943313 |
| 2 | 0.12 | 0.601050 | 0.96162903 | 0.9239213 | 0.9239212 | 0.18745786 |
| 3 | 0.24 | 0.616354 | 0.9428088 | 0.89377195 | 0.89377195 | 0.113351054 |
| 4 | 0.36 | 0.562797 | 0.89261997 | 0.88375837 | 0.88375837 | 0.42168635 |
| 5 | 0.44 | 0.650945 | 0.80568093 | 0.868855 | 0.8688551 | 0.70353 |
| 6 | 0.56 | 0.707987 | 0.89632505 | 0.9225719 | 0.92257196 | 0.7604736 |
| 7 | 0.68 | 0.774187 | 0.9662328 | 0.9245758 | 0.9245759 | 0.7607451 |
| 8 | 0.72 | 0.737558 | 0.91988695 | 0.94264454 | 0.9426444 | 0.82596755 |
| 9 | 0.80 | 0.861691 | 0.9639947 | 0.9695872 | 0.96958715 | 0.9212673 |
| 10 | 0.96 | 0.986756 | 0.9924786 | 0.9928368 | 0.99283665 | 0.9951408 |
| 11 | 1.00 | 0.885105 | 0.969366 | 0.9700116 | 0.97001165 | 0.97573876 |
| 12 | 1.00 | 1.000000 | 1.0 | 0.99999976 | 0.9999998 | 1.0000001 |
相関係数を計算する
上で計算した各種数値が JSTS データセットの label とどれくらい相関があるか調べます。
今回は以下の3種類を見てみました。
- Pearson 相関係数
- 2つの変数間の関係の強さと互いの関連性を測定するもの
- データが連続で正規分布に従っていると仮定する
- Spearman 相関係数
- 順位相関(2つの変数間の順位の統計的依存性)のノンパラメトリック尺度
- 順位をそのまま Pearson の式に当てはめるイメージ
- Kendall 相関係数
- 比較するペア同士の大小関係を +1 および -1 で数値化し、+1 および -1 の個数から相関を求める方法
- Spearman よりもロバスト $\Longrightarrow$ 外れ値が多かったりサンプル数が少なかったりすると Kendall の方が強い
詳しい説明は以下の記事を参照してください。
参考:
類似度の計算ではサンプルを抽出して計算結果を見ましたが、以下では JSTS データセットに含まれる valid データ全部(1457件)を使用します。
Peason 積率相関係数
from scipy.stats import pearsonr
x = df_sample['label']
cols = ['F1_BERTscore', 'cos_bert (CLS)', 'cos_bert (AVG)', 'cos_sbert', 'cos_sbert(fine-tuned)']
df_pearson = pd.DataFrame(columns=['有意確率 P 値', '相関係数'])
for col in cols:
r, p = pearsonr(x, df_sample[col])
df_pearson.loc[col] = [p, r]
| P 値 | 相関係数 | |
|---|---|---|
| F1_BERTscore | 0.0000 | 0.6841 |
| cos_bert (CLS) | 0.0000 | 0.3301 |
| cos_bert (AVG) | 0.0000 | 0.6869 |
| cos_sbert | 0.0000 | 0.6869 |
| cos_sbert(fine-tuned) | 0.0000 | 0.8611 |
- P値は $< 0.05$ で相関関係あり、$\geq 0.05$ で相関なし
- 相関係数は相関の強度
なので、Pearson 相関係数で見ると cos_sbert(fine-tuned) が最も JSTS データセットと相関が強い $\Leftrightarrow$ 最も再現できている、と言えそう
Spearman 順位相関係数
from scipy.stats import spearmanr
idxs = [*range(len(df_sample))]
x = sorted(idxs, key=lambda n: df_sample['label'][n]) # labelを順位に変換
df_spearman = pd.DataFrame(columns=['有意確率 P 値', '相関係数'])
for col in cols:
y = sorted(idxs, key=lambda n: df_sample[col][n]) # 該当列を順位に変換
r, p = spearmanr(x, y)
df_spearman.loc[col] = [p, r]
| P 値 | 相関係数 | |
|---|---|---|
| F1_BERTscore | 0.5870 | -0.0142 |
| cos_bert (CLS) | 0.6373 | -0.0124 |
| cos_bert (AVG) | 0.0413 | -0.0535 |
| cos_sbert | 0.0366 | -0.0548 |
| cos_sbert(fine-tuned) | 0.7968 | 0.0068 |
Spearman 相関係数で見ると、$P < 0.05 $ を満たすのは cos_bert (AVG) と cos_sbert だけだが、相関係数はほぼ $0$ なので、相関があるとは言えない。
Kendall 順位相関係数
from scipy.stats import kendalltau
idxs = [*range(len(df_sample))]
x = sorted(idxs, key=lambda n: df_sample['label'][n]) # labelを順位に変換
df_kendalltau = pd.DataFrame(columns=['有意確率 P 値', '相関係数'])
for col in cols:
y = sorted(idxs, key=lambda n: df_sample[col][n]) # 該当列を順位に変換
r, p = kendalltau(x, y)
df_kendalltau.loc[col] = [p, r]
| P 値 | 相関係数 | |
|---|---|---|
| F1_BERTscore | 0.5833 | -0.0096 |
| cos_bert (CLS) | 0.6258 | -0.0085 |
| cos_bert (AVG) | 0.0409 | -0.0358 |
| cos_sbert | 0.0360 | -0.0367 |
| cos_sbert(fine-tuned) | 0.8054 | 0.0043 |
Kendall 相関係数の方も、$P < 0.05 $ を満たすのは cos_bert (AVG) と cos_sbert だけだが、相関係数はほぼ $0$ なので、相関があるとは言えない。
散布図で確認する
Spearman と Kendall の順位相関係数が相関無の結果になったので、その理由を探してみます。
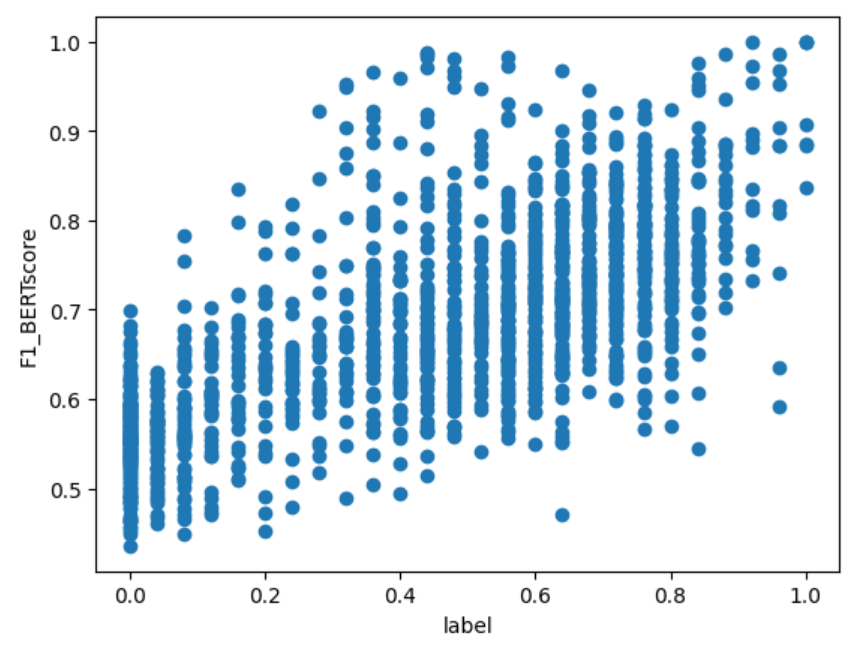
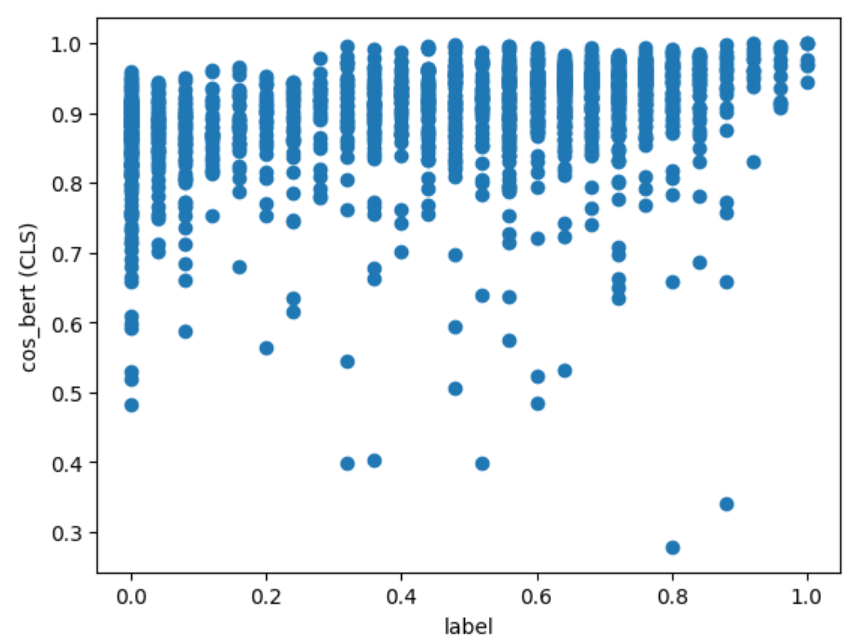
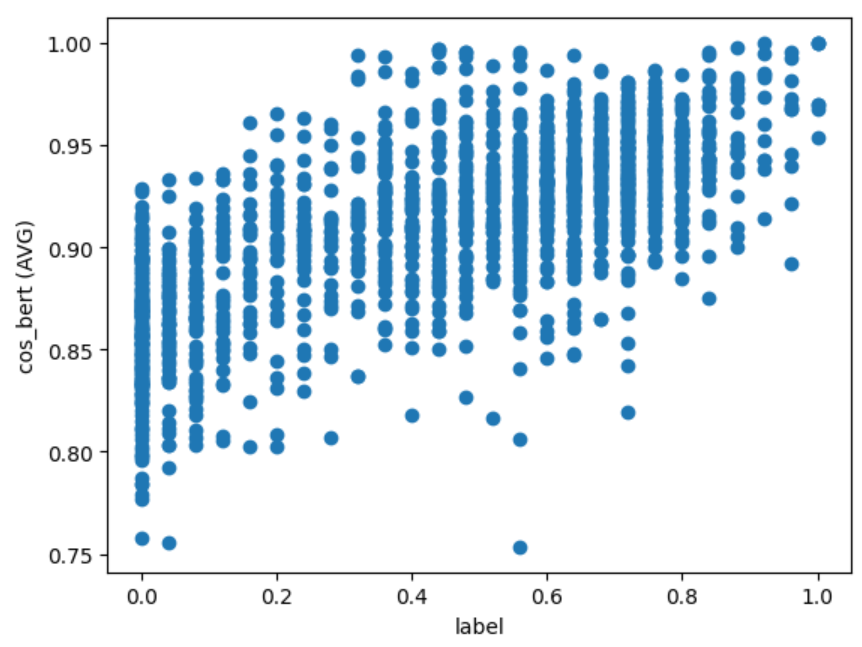
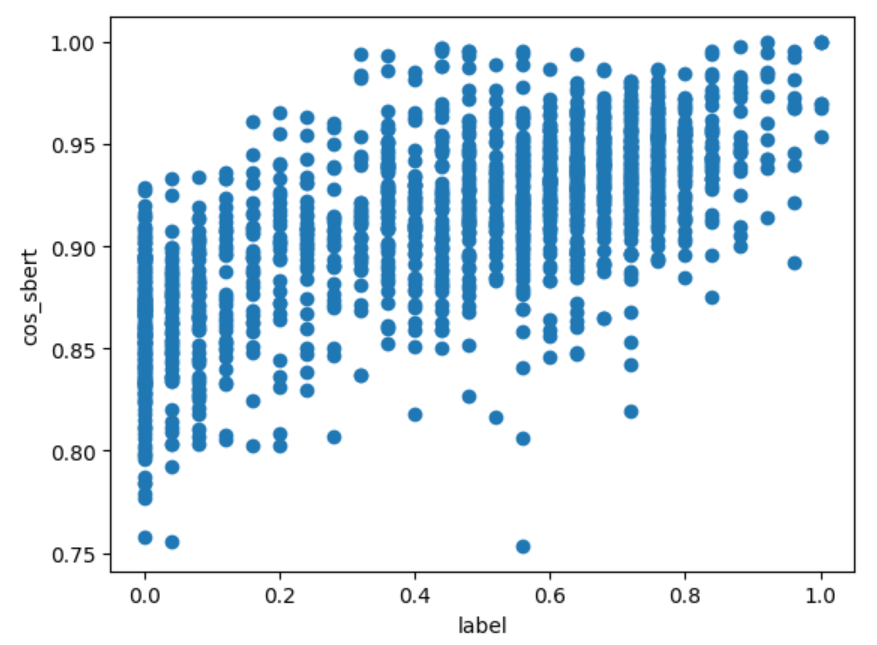
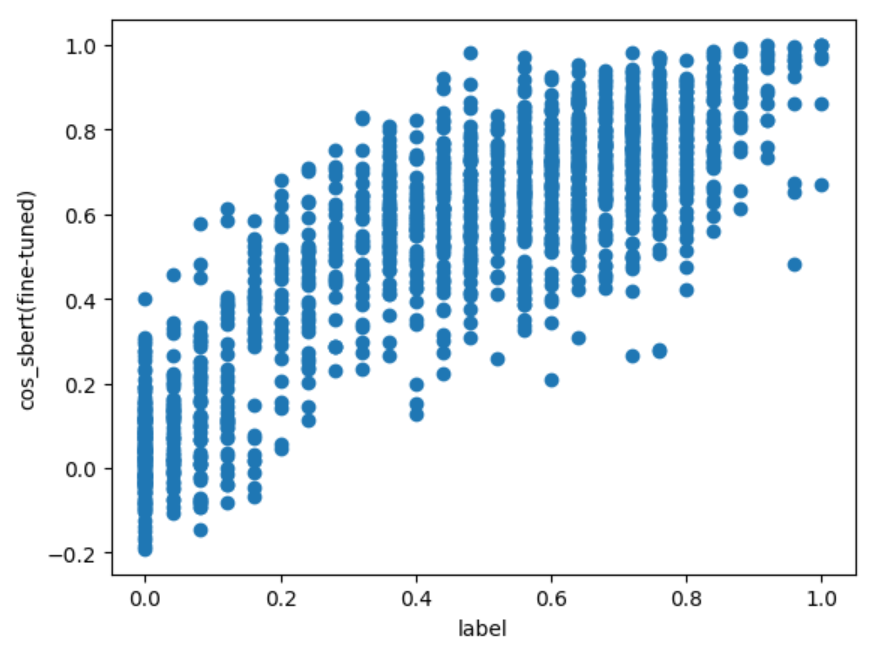
x 軸に JSTS データセットの label、y 軸に類似度の計算結果をとって各計算方法の散布図を出力すると、以下のようになりました。
上図から分かること:
- どれも分布の形としては label が高くなると類似度も高くなる傾向はある $\Longrightarrow$ Pearson 相関係数が良い結果になる
- label が同じデータでも文章ペアによって類似度の幅がある $\Longrightarrow$ 順位付けがうまくできずSpearman と Kendall の順位相関係数が相関なしの結果になる
- cos 類似度の値域は $[-1, 1]$ だが、マイナスまで出ているのは
cos_sbert(fine-tuned)のみ - どの計算方法も label が高い(類似している)文章ペアについては高い類似度が算出されている
- 一方で
cos_sbert(fine-tuned)以外は label が $0$ の(類似性のない)文章ペアについても高い値が出ている $\Longrightarrow$ cos の定義を考えるとベクトルが一定の領域(小さい角度)内でしか表現されていない模様
考察
今回の計算結果について:
- 人が同程度の類似と感じる文章ペアであっても、文章ベクトルの cos 類似度はかなり大きい幅で算出される
- cos 類似度に幅があるため順位付けが難しく、相関関係を見るには Peason 相関係数が向いていそう
- Peason 相関係数をみると、JSTS データセットの類似度をより再現できている計算方法は以下の順と言えそう
- cos_sbert(fine-tuned)
- cos_bert (AVG), cos_sbert
- F1_BERTscore
- cos_bert (CLS)
- SentenceBERT は attention mask を使ってベクトルを算出しているので文章の意味をうまく反映できているのかも
その他気付いたこと:
- Pytorch の cosine_similarity は同じベクトル同士で計算しても 1.0 にならない場合がある模様
今後の課題
- cos 類似度が狭い範囲に偏ってしまったのは、計算の仕方が悪いせいか調査する
- cos 類似度以外に類似度を表現できる良い方法を探す(複数の方法を組み合わせるなど)
- 他に良い評価方法がないか探す