はじめに
「株価や為替の予測って面白そうだな〜」「いくつか論文を読んでみようかな〜」から始まり, いくつか興味のありそうな論文や学会資料を適当にダウンロードして読んでたら, 個人的にものすごく面白そうな資料を見つけて感動しました.
そこで終わったらdame.
読むだけじゃなくて自分なりに実装してみようということで, 今まで株価や為替のデータに触れたこともなかったけど, データを取得して, 一応形にしてみました.
対象:
プログラミングの四則演算やif文, for文といった基本的なことはわかり, 株価や為替の分析に興味がある人向け.大学からプログラミングを始めた1, 2年生が読めるように書いてます.(既に高度な知識を持ち,様々な予測や解析を行える人向けではないです.(まず僕が書けない...笑))
概要:
k-medoids法を用いて過去のドル円をクラスタリングし, 正答率を求める, までの流れが記述してあります.
1 データの取得
今回はドル円の日足データを過去15年, 時間足データを過去5年分ぐらい取得しました.
データを取得できることすら知らなかったので, ここで結構手間取りましたが, 偶然「oanda api」なる存在を発見し, 使い方をまとめてあるQiitaを参考に, なんとか取得することができました.
取得した日足データはこんな感じ(下図).
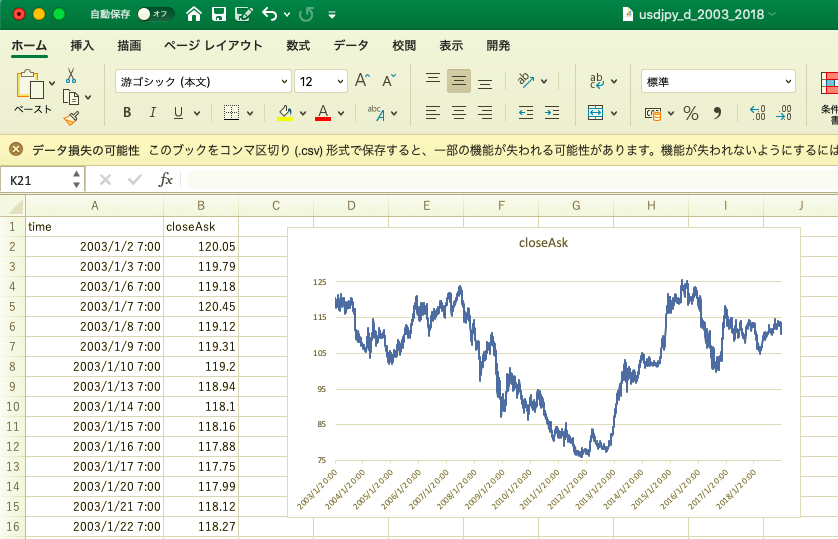
excelの方がなんとなく親近感が湧きます.
OANDA APIからデータを取得
僕は大量の為替過去データをFX APIから取得する方法(機械学習用)を参考にデータを取得しました.
APIを使えるようになるまでの手順で手間取ったので, 以下に手順を載せます.
まずoanda apiとはFX業者oandaが提供しているapiです.
使うためにはidとkeyが必要で, oandaのデモ口座を開設しなければなりません.
「oandaのホームページ」https://www.oanda.jp
ホームページから「新規口座開設」→「デモ口座 新規開設」を選択します.
無料デモ口座開設フォームで各種情報を入力し, デモ口座IDの発行. その後IDとパスワードが添付されたメールが送られてくるので, デモ口座にログインします.
下図真ん中部分の口座情報の中に「AccountID」があります.
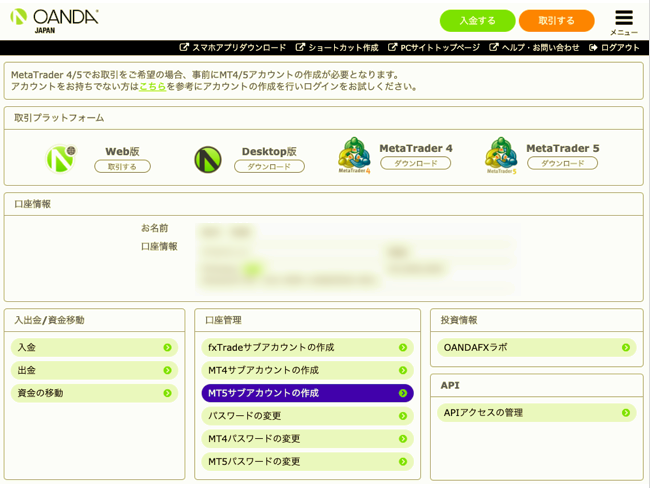
右下の「APIアクセスの管理」から入りPersonalAccessTokenを取得をしましょう.
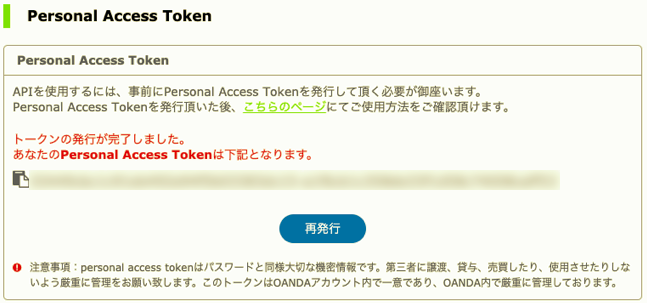
AccountIDとAccessKey(PersonalAccessTokenが取得できればこれでAPIを使用することができます.
oandapyというパッケージをインストールして
pip install git+https://github.com/oanda/oandapy.git
為替の情報を取得します.
必要なライブラリを読み込み, 試しに現時点のドル円レートを取得してみます.
import pandas as pd
import oandapy
import configparser
import datetime
from datetime import datetime, timedelta
import pytz
account_id = "xxxxx"
access_key = "xxxxx"
# oandaAPIの呼び出し
oanda = oanda.API(access_token = access_key, environment = "practice")
# 今の時間のドル円レートを取得
res = oanda.get_prices(instruments = "USD_JPY")
出力結果↓↓↓
{'prices': [{'ask': 107.321,
'bid': 107.317,
'instrument': 'USD_JPY',
'time': '2020-03-05T06:12:23.365940Z'}]}
コロナウイルスの影響で112円台から107円台に暴落してますね.
ここから先は大量の為替過去データをFX APIから取得する方法(機械学習用)にものすごくわかりやすく書いてあるので, この記事を参考に希望する期間のデータを取得してください.
2 分析方法
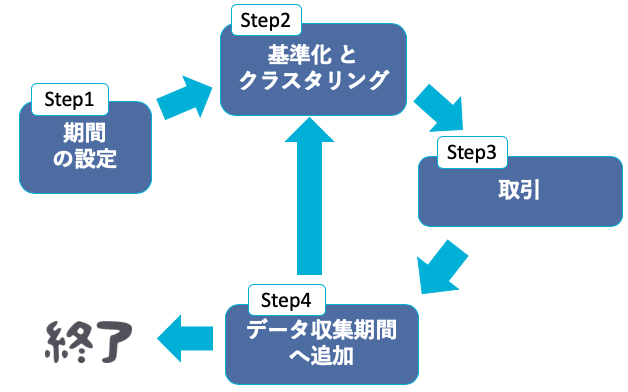
以下のStepに沿って分析を行います.
Step1:予測期間, データ収集期間, 検証期間を決める
Step2:データ収集期間のクラスタリングを行う
Step3:検証期間のうち, 予測期間の取引を行う
Step4:行った取引期間のデータを, データ収集期間へ追加
Step5:検証期間が終わっていない時Step2に戻り, 検証期間が終わっている時終了する.
それぞれの期間は次の意味を持っています.
データ収集期間:過去の値動きを参照する期間.(一般的に訓練データ)
検証期間:正答率を評価する為の期間.(一般的にテストデータ)
予測期間:来月,来週,明日どうなるのか?という予測をする期間(月毎, 週毎, 日毎の3つを用意した)
例として予測期間を月毎, データ収集期間を2003~2015年末までの156ヶ月, 検証期間を2016~2018年末までの36ヶ月とする.(一度理解すればあとは期間を変えるだけ)
図にするとこんな感じ.(下図)
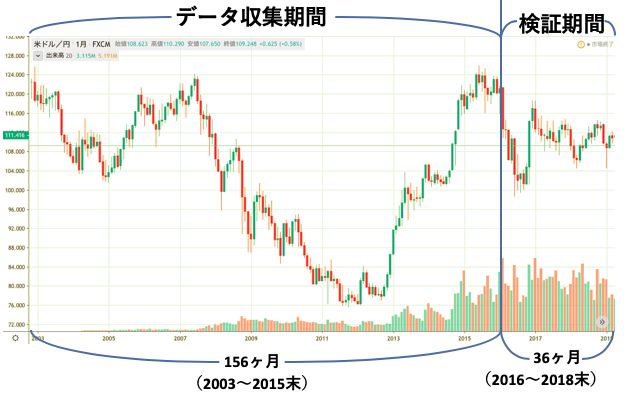
Step2でk-medoid法をデータ収集期間に適用します.
イメージとしては「データ収集期間をいくつかのパターンに分けた際, これから予測する期間はどのパターンになるだろうか」です.
なのでまずデータ収集期間をいくつかのパターンに分類します.
チャートの値動きは基本的に上昇, 横ばい, 下落の3パターンに分類されるので, ここでは3つのクラスに分類します.
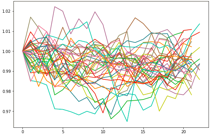
156ヶ月の値動きをまとめてみるとこんな感じになります.(下図)
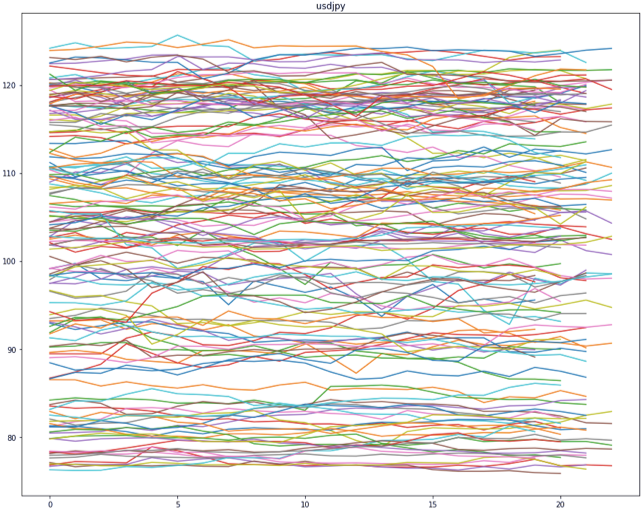
系列数は156本で, 要素数にばらつきがある理由は, 30日で終わる月や31日で終わる月,2月といった違いがあるからです.
また外国為替は休日や元旦は取引されないので, 各系列の要素数は18~22ぐらいになります.
各系列の特徴を把握する為, それぞれ期初の値(要素[0])で各要素を割ってあげます. するとこんな感じになります.(下図)
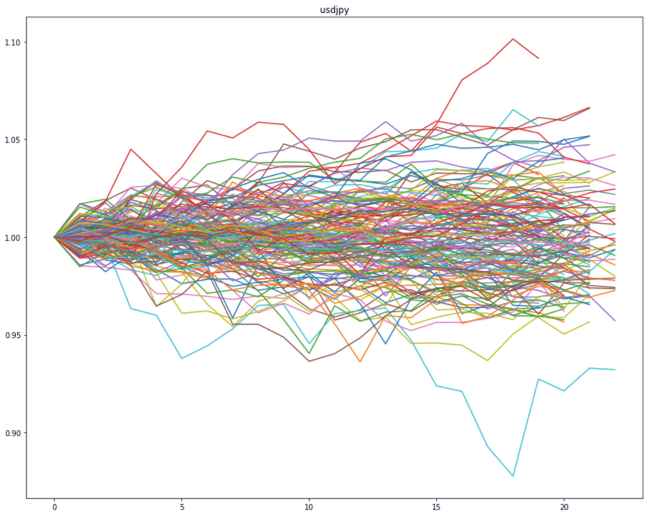
DTW距離
それでは次にこのこんがらがってる系列たちを3つに分類してあげます.
しかしここで問題になるのが,どうやって分類するのか?です. 時系列の形状をそれぞれ定量的に評価できるのか?と思っていましたが, DTW距離という測定方法を使えば解決することができます.
これはDTW関数の中に比較したい2つの時系列を入れると値が返ってくるもので, これを利用して各時系列間を定量的に評価することができます.
AとBの時系列をDTW関数の中にいれると297となります.

A~Eまでの全ての組み合わせでDTW関数を求めると下の表のようになり,
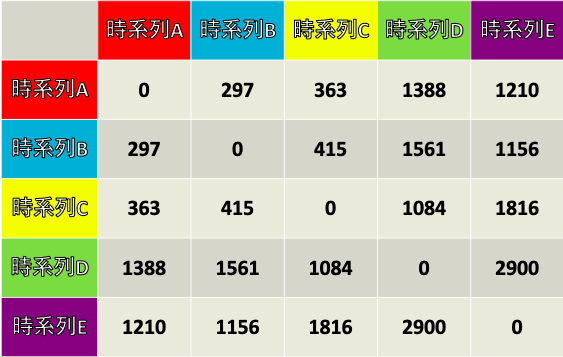
一番近い時系列AとBのDTW距離は297, 一番遠い時系列DとEのDTW距離は2900と, グラフを見たときに近い, 離れてると認識した情報を定量的に評価できます.
DTWのアルゴリズム, コード
アルゴリズムは次のようになります.
Step1:各点の絶対値の差を求めた長さM×長さNのCost行列を作成
Step2:M×NのDist行列を作成, $Dist{(1, 1)} = Cost{(1,1)}$, 他要素に$∞$を代入して初期化.
Step3:Dist行列の1行目, 1列目は1つ前の値と, 同じ位置のCost行列の値を足す.
Step4:次の式にしたがってDist行列を作成.
Dist_{(i, j)} = Cost{(i, j)} + min(Dist{(i, j-1)}, Dist{(i-1, j)}, Dist{(i-1, j-1)})
Step5:$Dist{(M,N)}$をDTW距離とする.
まずAとBの時系列に着目し, DTW距離を計測する場合どのようになるのか.
Step1より各点の絶対値の差を求めたCost行列を作成し, Step2, Step3よりDist行列を初期化し, Step4に従ってDist行列を作成すると, 以下のようになります.
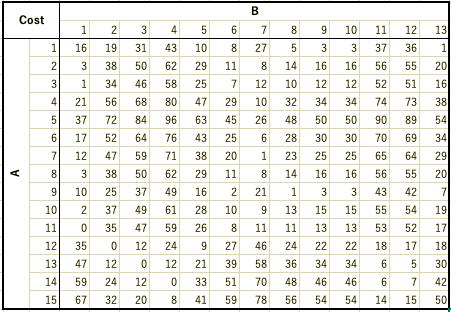
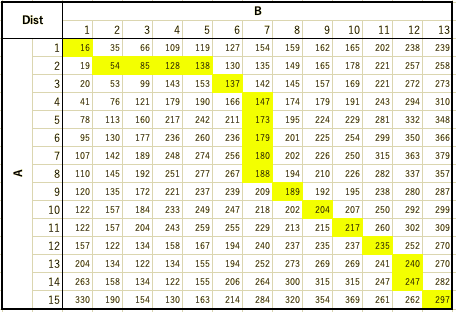
Step5より時系列AとBのDTW距離は297と求められる.
これらを関数にしたものが以下.
# dtw距離を求める関数
def dtw(x, y):
#距離行列を作成する。
X, Y = np.meshgrid(x, y)
dist = abs(X-Y) #ユークリッド距離
#print(dist)
#dtwを計算する行列の初期化
#dtwのアルゴリズム上, dtw[-1][-1]を最初に参照してしまうため, 行, 列共に元の時系列の長さ+1のdtw行列を確保
dtw = np.full((len(y) + 1, len(x) + 1), np.inf)
dtw[0, 0] = 0
for i in range(1, len(y) + 1):
for j in range(1, len(x) + 1):
dtw[i, j] = min(
dtw[i - 1, j],
dtw[i, j - 1],
dtw[i - 1, j - 1]) + dist[i - 1, j - 1]
return dtw[-1, -1]
dtw関数を使って, 各時系列間のdtw距離値を格納したdtw行列を作成する.(上に載せたA~Eまでの全ての組み合わせが入った表のこと).
def make_dtw_matrix(data):
dtw_matrix = [[0 for i in range(len(data))] for j in range(len(data))]
for i in range(0, len(data)):
for j in range(0, len(data)):
dtw_matrix[i][j] = dtw(data[i], data[j])
return dtw_matrix
k-medoids法
次にいよいよk-medoids法を用いてクラスタリングを行います.
k-medoids法とはk-means法と類似した分割最適化クラスタリングの手法で, k-means法では基点を重心(centroid)にしますが, k-medoids法では割り当てられたクラスの中で, 他全ての点との距離の合計が最小となる点を基点(medoids)とします. その為, k-means法では重心の計算方法から, 外れ値の影響を受けやすいという欠点がありますが, k-medoids法では基点(medoids)にクラスないのデータの1つが割り当てられるので, 外れ値の影響が少なくなるという利点があります.(k-means法を引き合いに出しましたが, 知らなくてもこの記事は読めるので大丈夫です.)
DTW距離によって時系列間の距離を数値化し, k-medoids法を使って数値化されたdtw行列を分類します.
3つのクラスに分類するとこんな感じ.(下図)
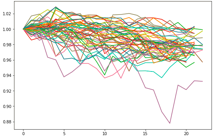
なんとなく横ばいクラス(53系列), 下落クラス(66系列), 上昇クラス(37系列)に分かれています.
k-medoids法のアルゴリズム, コード
アルゴリズムは次のStepで進みます.
Step1:k個のクラス数分の点をランダムに選択する.(medoid)
Step2:各点を各々一番近いmedoidのクラスに割り当てる.
Step3:それぞれのクラス内の他の全ての点との距離の合計が最小になる点を新たにmedoidとする
Step4:変化がなければ終了し, 変化があればStep2に戻る.
コードは以下に掲載します.
例として, 先ほどのA~Eの時系列を, クラス数を2つ分類するとどうなるのか?をやっていきます.
dtw行列は上記表の5×5の対角成分0の対称行列.
まずStep1でランダムに2つの系列を選択します.ここではAとBの系列をmedoidに選択しましょう.
コードではinitialize_medoidsに該当します.
medoidとはそのクラスの中で, クラス内全ての点との距離の合計が最小になるもの, です.
ですので2つに分類する今回は, medoidが2つできます.
medoidを格納したmedoidsは, medoids=[A, B](プログラム上はmedoids=[0, 1])になっています.
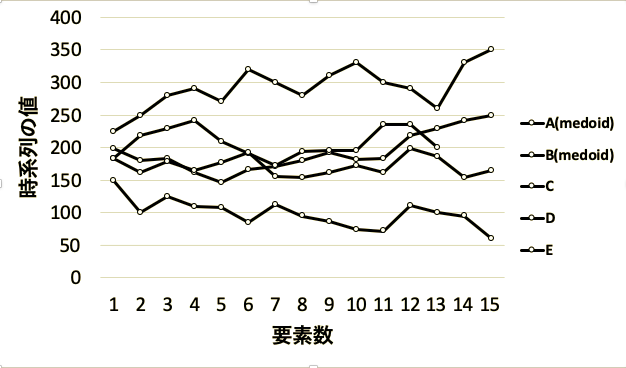
Step2各系列(A~E)を各々一番近いmedoidのクラスに割り当てます.
コードではassign_to_nearestに該当します.
ここでは割り当てられたクラスをラベル(label)と表記し, 2つのクラスに分類するのでラベル「0」とラベル「1」の2つ用意することとします. まだ何もしていないので, 現在の各系列に割り振られたラベルはlabel = [?, ?, ?, ?, ?](プログラ上はlabel=[∞, ∞, ∞, ∞, ∞])です.
dtw行列に注目して, medoidに選択された系列はAとB.ラベル0のmedoidが今は系列A, ラベル1のmedoidが今は系列B, です.
各系列がどちらのmedoidに近いのかを見てみると以下の赤丸になります.
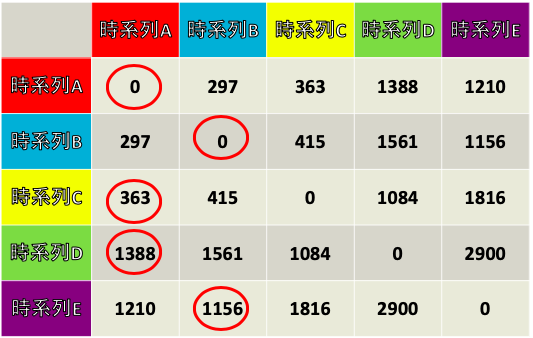
よって各系列にとって一番近いmedoidが割り振られたラベルはlabel=[0, 1, 0, 0, 1]となりました.
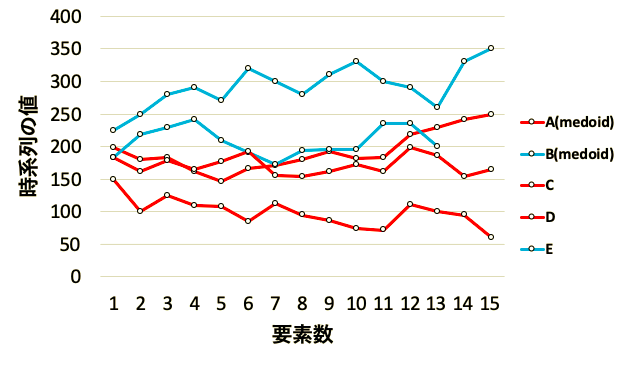
Step3:それぞれのクラス内の他の全ての点との距離の合計が最小になる点を新たにmedoidとする.
コードではupdate_medoidsに該当します.
クラス内の各系列に着目し, その系列からクラス内の他全ての系列との距離の合計が最小になる値を格納するmindist, 新しいmedoidを格納するmedoidsを用意します.
ただいまmindist=[?, ?], medoids=[?, ?]の状態です.
それではA~Eに対して, どのラベルに割り振られているのか?, 他のラベルとの距離の合計はいくらか?を求めて, 他のラベルとの距離の合計が一番小さい系列を新たなmedoidに更新しましょう.
まず系列A.
系列Aはラベル0, 他に0に割り振られた系列は系列Cと系列D. dtw行列から値を確認すると下の赤丸に該当します.
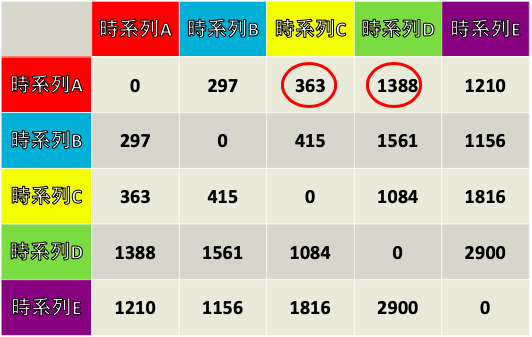
363+1388=1751なので, mindist=[1751, ?], medoids=[0, ?]となります.
系列B.
系列Bはラベル1, 他に1に割り振られた系列は系列Eのみなのでdtw行列から値を確認すると1156.
よってmindist=[1751, 1156], medoids=[0, 1](ここまではさっきと変わってない)
系列C.
系列Cはラベル0, 他に0に割り振られた系列は系列Aと系列Dなのでdtw行列から値を確認すると, 合計1447(363+1084).
これは1751よりも小さいため, mindist=[1447, 1156], medoids=[2, 1]と更新する.
系列Dはラベル0, 同様にdtw行列から値を確認すると, 合計2472となり, mindistを更新しないためスルー.
系列Eはラベル1, 同様にdtw行列から値を確認し, mindistを更新しないためスルー.
以上よりmedoidが[0, 1]から, [2, 1]に更新されました.
この新たなmedoidに, Step2と同様の手順で各系列にとって一番近いmedoidに割り振ってあげると
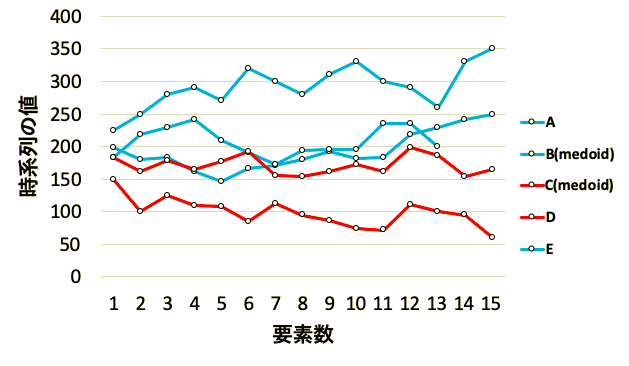
良い感じに分けることができてます.
説明が冗長でわかりにくいところが多いと思うのですが, 以上の手順をmedoidが更新されなくなるまで繰り返し行い分類をするのがk-medoids法です.
以下pythonで記述したk-medoids法のプログラムです.(ここまで書きましたが, ライブラリが用意されているのでそっち使った方が楽...)
# kmedoids法のアルゴリズム
def kmedoids(dtw_matrix, total_class_num):
medoids = initialize_medoids(dtw_matrix, total_class_num)
label = [0 for i in range(len(dtw_matrix))] #len(dtw_matrix)の長さの0が入っている, つまり今はすべての時系列のラベルが0
for i in range(0, 100):
new_label = assign_to_nearest(dtw_matrix, medoids)
if new_label == label:
break
label = new_label
medoids = update_medoids(dtw_matrix, label, total_class_num)
return (label, medoids)
def update_medoids(dtw_matrix, label, total_class_num):
n = len(dtw_matrix)
mindists = [np.inf for i in range(total_class_num)] #クラス数分のinfを持つ配列. k=3 なら [inf, inf, inf]
medoids = [np.inf for i in range(total_class_num)]
for i in range(0, n):
ts_label = label[i]
dist_total = 0
for j in range(0, n):
if label[j] == ts_label:
dist_total += dtw_matrix[i][j]
if dist_total < mindists[ts_label]:
mindists[ts_label] = dist_total
medoids[ts_label] = i
return medoids
def assign_to_nearest(dtw_matrix, medoids):
total_class_num = len(medoids)
label = [0 for i in range(len(dtw_matrix))]
for i in range(0, len(dtw_matrix)):
mindist = np.inf
nearest = 0
for j in range(0, total_class_num):
if dtw_matrix[i][medoids[j]] < mindist:
mindist = dtw_matrix[i][medoids[j]]
nearest = j
label[i] = nearest
return label
def initialize_medoids(dtw_matrix, total_class_num):
medoids = list(range(len(dtw_matrix)))
return medoids[0:total_class_num]
取引
次に取引を行います.
予測する系列の1つ前の系列に注目して, その系列がどのクラスに所属するのかを確認します.
そのクラスの半分以上の系列が上昇(下落)していた場合, 将来上昇(下降)すると予測し, 買い(売り)の判断をします.
実際に少しでも上昇していたら成功とカウントし, 予測した期間をデータ収集期間の中に格納して再度クラスタリングを行います.
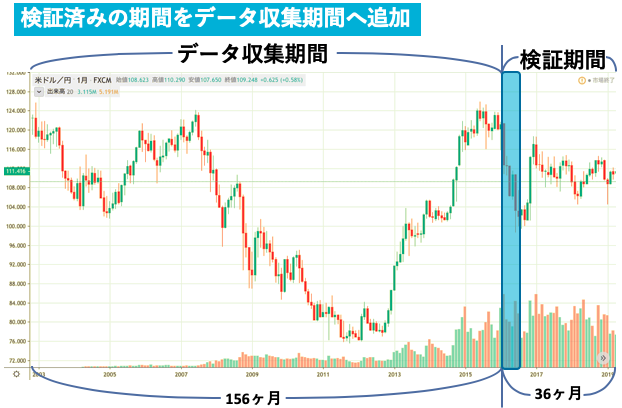

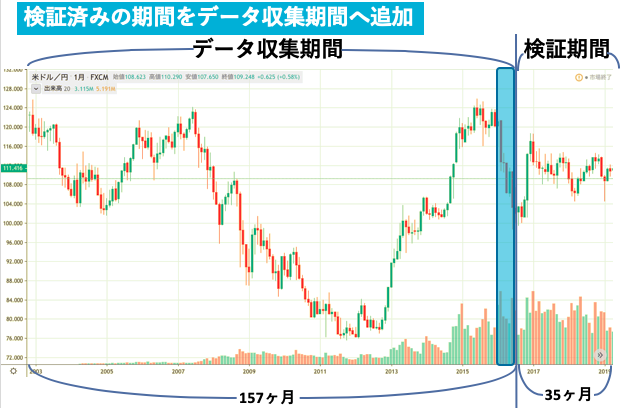
先ほどの例でいうと, 検証期間(2016~2018末)の1つ目である2016年1月を予測する場合は, 1つ前の系列である2015年12月の系列の分類されたクラスを確認. そのクラスに従って取引, 終了後2016年1月の系列をデータ収集期間の中に格納し再度クラスタリング, 次に2016年2月の系列を予想する, という流れです.
このようにデータ収集期間と検証期間を色々工夫したり, 予測期間を変えたりして正答率を求めました.
3 分析実行
コードを書き終えたとき, これで精度良く分析できたらお金持ちになれるじゃん!とワクワクしてました.
が, そんなに甘くありませんでした.
結果は次のとおりです.
予測期間:月毎
予測期間:週毎
予測期間:日毎
クラス数は3から7の5パターンに限定(増やしてもあまり変わらなかった)して結果を出しました.
どの結果も40~50%程度の正答率になっていて, ちょっとガッカリ.
しかしまだ改良の余地はたくさんあります.
取引方法を見直し, 2つの仮説を考えて実装したところ, 予測期間が週毎では平均して65%程度の正答率にすることができました.
これはまた別の記事にまとめようと思っています.
実行時間が長い!
とても長いです. 予測期間が日毎のケースでは一回実行するのに100分程かかってます. もっと早く結果を出したいなぁと思いました.
僕はMacBookAir(Early2015), プロセッサ1.6GHz デュアルコアIntel Core i5, メモリ8GBの特にカスタムしてないものを使っているのですが, 先日新しいパソコンを購入しました.
スペックはCPU:Corei7-9850H(2.6GHz, 6コア), メモリ:16GB, NVIDIA GeForce MX150(GPU)です.
このプログラムの他に書籍などを参考にした機械学習プログラムをMacBookAirとGPU搭載のノートパソコンで実行させたとき, どのくらい時間の差が出るのかってことを比較してみようかなって考えてます.
参考文献
・大量の為替過去データをFX APIから取得する方法(機械学習用)
・株価変動パターンの類似性を用いた株価予測
・価格変動パターンを用いた市場予測k-Medoids Clustering with Indexing Dynamic Time Warpingの株式市場への適用
・価格変動パターンによる証券/為替/仮想通貨市場の分析