ボウリングの新しいスコア計算についての考察

Abstract

本記事はボウリングの従来のスコア計算法と新しい計算法でスコアにどれほど差が出るのかをPythonでシミュレーションした. すると、レベルが異なる3つのボウラーで実験してみると　いずれも20ピン程度スコアが高くでてくることがわかった.

Introduction

みなさん初めましてmasa10223 です. 突然なんですが皆さんはボウリングをしたことはありますか？
これを読んでいる皆さんのほとんどが一度はボウリングをしたことはあると思います.
「なかなかボールがレーンに乗らない」
「最高点200超えたことがある」
「いやいや100点全然超えない」
いろんな感想をお持ちだとは思いますが、
「スコア計算がややこしい」」
という感想をお持ちの読者も一部はいると思います.

従来のスコア計算法

ここでボウリングの従来のスコア計算についておさらいしてみましょう.
まず、ボウリングは10本のピンがたっていて、
一投目で10本全てを倒すストライク、一投目で残ったピンを倒すスペア、そしてそれ以外をオープンから構成されています.
またストライクやスペアを取ることを通称マークをつけると表現したりもします.
ボウリングは10フレームあり　9フレーム目までは最高二投ずつ投げることができますが10フレームだけマークをつけると3投目を投球することができます.
そしてスコアの計算法ですが、3つの原則で計算されます.

1. ストライクを出すと次の2投で倒したピンの本数+10本がストライクを出したフレームの点数になる.
2. スペアを出すと次の1投で倒したピンの本数+10本がスペアを出したフレームの点数になる.
3. オープンをした場合はそのフレーム2回で倒したピンの本数がフレームの点数になる.

では実際に計算をしてみましょう. Xはストライク、/はスペア、Gはガターを表します.

1	2	3	4	5	6	7	8	9	10
X	9/	9-	X	X	63	9/	G /	X	XX9
20	39	48	74	93	102	112	132	162	191

いかがでしょうか. 最初の1フレームは ストライクの後 9+1=10 本倒しているので　10+10 =20がつきます
次のフレームはスペアなので3フレーム目の一投目に倒したピン+10 = 9+ 10=19が点数に加算されます.
以下同様に計算していきます.
ただし10フレームに関しては注意が必要で9フレームの点数に10フレームで倒したピンの総本数が加算されます. これでスコアの計算が終了です.

　ボウリングの新しいスコア方式とは？

以上のように従来のボウリングのスコアは次に投げる時のピンの倒れた本数を気にしなければならず計算がやや煩雑になります. そこでボウリングの新しいスコア計算法が提案されました.
その名もカレントフレーム方式です. この計算法は非常に簡単で、

1. ストライクを出すと30点がフレームの点数になる.
2. スペアを出すとそのフレームの一投目に倒したピンの本数+10点がフレームの点数になる.
3. オープンをした場合はそのフレーム2回で倒したピンの本数がフレームの点数になる.
4. 10フレームは他のフレームと区別しない.

というものになっています.
10フレームも最大で2投というのも大きな違いです.
カレントフレーム方式は計算の簡略化を図り導入が検討されていて、先月のインドネシアのパレンバンで行われたアジア競技大会でもそのスコア方式が導入されました.

この方式だと先ほどのスコアはどのように計算されるのでしょうか?　ただし、10フレームは他のフレームと区別しないということから10フレームはストライクにします.

1	2	3	4	5	6	7	8	9	10
X	9/	9-	X	X	63	9/	G /	X	X
30	49	58	88	118	127	146	156	186	216

となっています. 計算が単純でわかりやすい上に点数もでるのが特徴だと思います.

Background

このカレントフレーム方式は単発のストライクが従来のターキー(3連続ストライクのこと)に相当するので、ご覧のように点数が出やすくなっています.　
最近導入されたものの、一般人はおろかボウラーですら馴染みの薄いこのカレントフレーム方式が従来と比べてどれぐらい点数に差が出るのかをさまざまなレベルのボウラーのデータを用いて、シミュレーションで比較してみようと思い、この記事を書きました.

Method

計算法の実装

今回はPython 3.0 で実装してみました.使うmoduleはnumpy と matplotlibです.

import numpy as np
import matplotlib.pyplot as plt

まず従来のスコア計算法(以下、Original)を実装しました.

def Original_Score(a): #a is a list of pinfalls in every frames 
    score = 0 
    frame = 1
    if len(a) <11 : #bolwer must throw more than 10 times.
        print('error score format')
    for i in range(0, len(a)):
        while frame <= 10:
            if a[i] == 10 : #strike 
                score += a[i] + a[i+1] + a[i+2]  #2 pinfalls after strike add  
                i += 1 
                frame += 1 #1frame goes.
            elif a[i] + a[i + 1] == 10 : #juding spare
                score += a[i] + a[i+1] + a[i+2] #a pinfall after spare add
                i += 2 
                frame += 1 #1 frame goes.
            elif a[i] + a[i + 1] > 10: #error
                print("it's not right pinfalls!")
                print(str(frame)+'th frame') #print where bugs happen
                break
            else: #open frame
                score += a[i] + a[i+1]
                i += 2
                frame += 1 #1 frame goes
    return score

次に新しいスコア計算法(以下　Current)を実装します.

def Current_Score(a): #a is a list of pinfalls in every frames 
    score = 0 
    frame = 1 
    if len(a) <10  : #bolwer must throw more than 11 tiimes.
        print('error score format')
    for i in range(0, len(a)-1):
        while frame <= 10: 
            if a[i] == 10: #strike
                score += 30 #30 pins add when one strike 
                i += 1
                frame += 1
            elif a[i] + a[i+1] == 10: #spare
                score += a[i] +10 #fist pinfall and 10 pins add when spare
                i += 2
                frame += 1
            elif a[i] + a[i + 1] > 10: #error
                print("it's not right pinfalls!")
                print(str(frame)+'th frame')
                break
            else: #open frame
                score += a[i] + a[i+1]
                i += 2
                frame +=1
    return score

これで完成です.

ボウラーの実装

次に倒したピンのlistを作成するボウラーの実装をします.
まず最初に東京大学ボウリング部元主将、ボウリング歴5年目の筆者のデータを元にモデルを作成します.

参考にしたのはBest Bowlingさんのアプリで記録した2018/1/1 から 2018/10/31までの計800ゲームの全ての投球データです.

def my_bowling():　#model of my bowling data 
    frame = 1
    a = [] #list 
    while frame <= 10:
        pinfall = np.random.choice([10, 9, 8, 7,6,5], p=[0.50, 0.27, 0.10, 0.08, 0.04, 0.01]) #my bowling data of 2018 
        if pinfall == 10:
            a.append(pinfall)
            frame += 1
        if pinfall == 9 : 
            spare = np.random.choice(2,p=[0.15, 0.85]) #single pin cover percentage is 85%...
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 8:
            spare = np.random.choice(3,p=[0.10, 0.27, 0.63])
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 7:
            spare = np.random.choice(4 ,p=[0.05,0.18 ,0.32 ,0.45])
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 6:
            spare = np.random.choice(5 ,p=[0.01,0.05 ,0.23 ,0.26,0.45])
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 5:
            spare = np.random.choice(6 ,p=[0.01,0.01 ,0.30, 0.43 ,0.05,0.20])
            a.extend([pinfall,spare])
            frame += 1
    else:
        if a[-1] != 10: #if bowler cannot strike in 1st shot at 10th frame.
            if a[-2] + a[-1] == 10: #if bowler spare at 10 th frame, he can throw one more shot in original score system
                pinfall = np.random.choice([10, 9, 8, 7,6,5], p=[0.50, 0.27, 0.10, 0.08, 0.04, 0.01])
                a.append(pinfall)
        else: #if bolwer strikes in 1st shot at 10th frame ,he can throw 2 times in original score system
            pinfall = np.random.choice([10, 9, 8, 7,6,5], p=[0.50, 0.27, 0.10, 0.08, 0.04, 0.01]) #my bowling data of 2018
            if pinfall == 10:
                pinfall_2 = np.random.choice([10, 9, 8, 7,6,5], p=[0.50, 0.27, 0.10, 0.08, 0.04, 0.01]) #10th frame final shot
                a.extend([pinfall,pinfall_2])
            if pinfall == 9 :
                spare = np.random.choice(2,p=[0.15, 0.85])
                a.extend([pinfall,spare])
            if pinfall == 8:
                spare = np.random.choice(3,p=[0.10, 0.27, 0.63])
                a.extend([pinfall,spare])
            if pinfall == 7:
                spare = np.random.choice(4 ,p=[0.05,0.18 ,0.32 ,0.45])
                a.extend([pinfall,spare])
            if pinfall == 6:
                spare = np.random.choice(5 ,p=[0.01,0.05 ,0.23 ,0.26,0.45])
                a.extend([pinfall,spare])
            if pinfall == 5:
                spare = np.random.choice(6 ,p=[0.01,0.01 ,0.30, 0.43 ,0.05,0.20])
                a.extend([pinfall,spare])
    return a

np.random.choice をもちいて各フレームで一定の割合でピンを倒すかを選び、ストライクなら10をlistにappend し、ストライク以外ならどの確率でカバーをするかを選び、2つの数字をlistにextendする、という仕組みになっています.(冗長なコードでごめんなさい...)

データによると、
僕のストライク率はちょうど50%でした 9本以上を倒す確率は77%だそうです.
また簡単のため、一投目のカウントが5本未満になる確率は0%としました.

simulationの実装

最後にmodelを動かして実際にsimulateさせます.
modelに投球をさせてlist を吐かせたら、それをOriginalとCurrentで計算させてそれぞれの計算結果をlistに入れて histgramを描かせる. というものです.
のちの計算のために計算結果が書かれたlistを返します.

def score_simulation(epochs, model): #simulate bowling score
    original_score_list =[] #make score list of original score system
    current_score_list =[] #make score list of current score system
    for i in range(epochs):
        PINFALL = model() #set your model output is pinfall list
        original_score = Original_Score(PINFALL) #output is original score system
        current_score = Current_Score(PINFALL) #output is current score system
        original_score_list.append(original_score)
        current_score_list.append(current_score)
    fig = plt.figure(figsize=(20,20)) #figure size
    plt.hist(original_score_list, histtype="barstacked",label='original',bins=30,alpha=0.7) #plot histgram of original
    plt.hist(current_score_list, histtype="barstacked",label='current',bins=30,alpha=0.7) #plot histgram of current
    plt.xlabel('score')
    plt.ylabel('frequency')
    plt.savefig('./Current_and_Original_.png') #save figure
    plt.legend() #show the legend
    plt.show()　#show the figure 

    return original_score_list, current_score_list

最後に、Current と Original でどれぐらいの差が出るのかを知るための関数を定義します (先ほどのsimulationの関数に組み込むのでもいいですが、個人的にplotデータと計算結果を分けたい主義なので別にしました.)

def analysis_of_score(original_score_list,current_score_list):
    from statistics import mean, median,variance,stdev

    original_ave = mean(original_score_list) #average of original score
    current_ave = mean(current_score_list) #average of current score

    original_med = median(original_score_list) #median of original score
    current_med = median(current_score_list) #median of current score

    original_var = variance(original_score_list) #variance of original score
    current_var = variance(current_score_list) #variance of current score

    original_stdev = stdev(original_score_list) #standard devaition of original score
    current_stdev = stdev(current_score_list) #standard deviation of current score

    print("We simulate your bowling score in each scoring system")
    print("Original Score System:"+"your average is:"+str(original_ave)+"\tmedian is :"+str(original_med)+"\tvariance is:"+str(original_var)+"\tstdev is:"+str(original_stdev))
    print("Current Score System:"+"your average is:"+str(current_ave)+"\tmedian is :"+str(current_med)+"\tvariance is:"+str(current_var)+"\tstdev is:"+str(current_stdev))

    #############################################################################
    #check how differ from original and current score system in each game       #
    #Suppose Current score is higher than Original Score, I define a constant   #
    #which indicates "difference" from Current and Original                     #         
    #############################################################################
    assert(len(original_score_list) == len(current_score_list)) #check the length

    diff_list = []
    for i  in range(len(original_score_list)):
        diff = (current_score_list[i] - original_score_list[i])
        diff_list.append(diff)
    diff_ave = mean(diff_list) #average of "difference"
    if diff_ave > 0: # Current is higher than Original
        print("Current score is "+str(diff_ave)+"pin higher than Original score in each game!!")
    else:
        print("Current score is "+str(-diff_ave)+"pin lower than Original score in each game!!")

これで準備は完了です. simulationを回しましょう.

Results

筆者の場合 (中級者)

まず自分のModelでやってみました.
epoch は 3000ぐらいで回したところ、

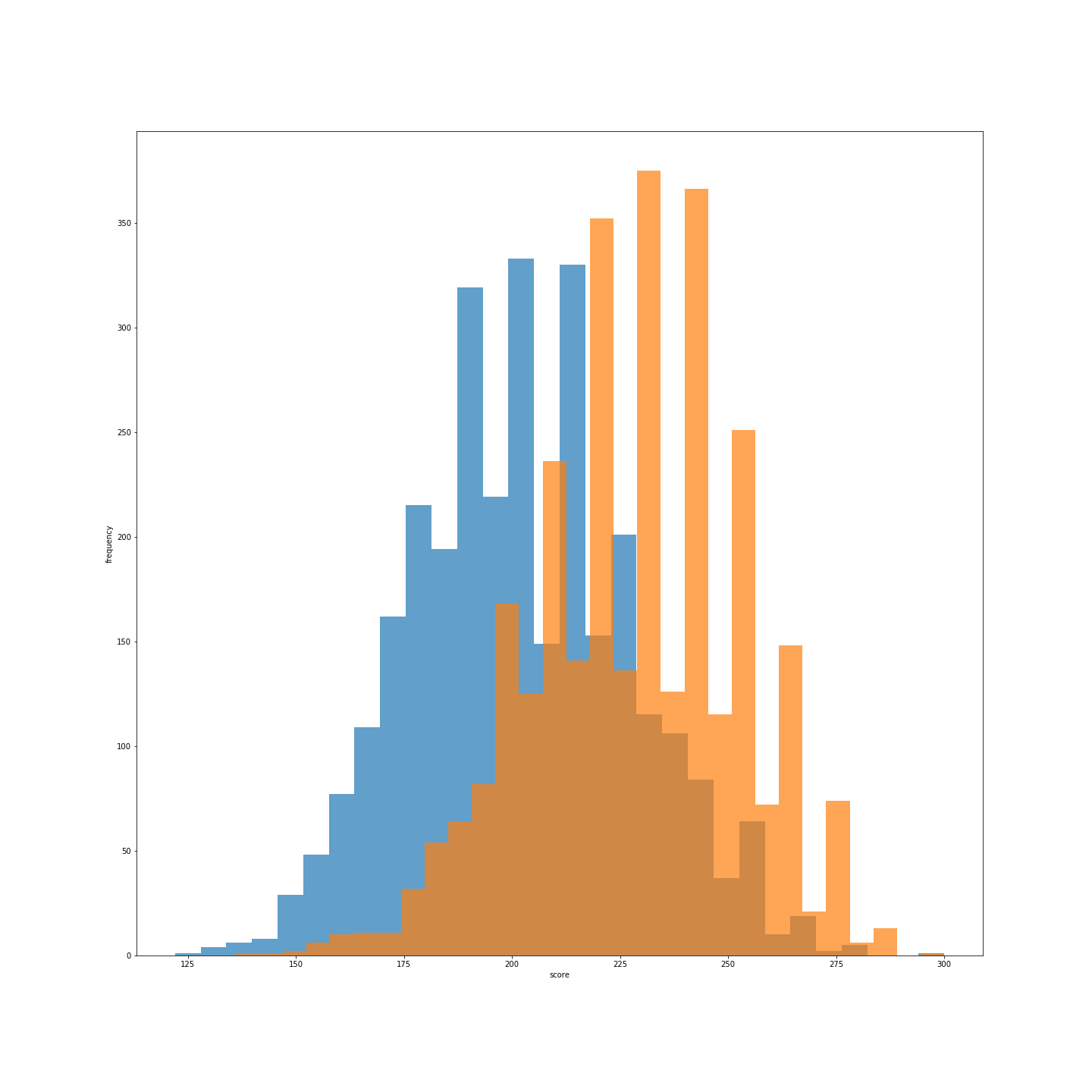
という結果が得られました　青がOriginal　で　橙がCurrent で全体的にCurrentの方が右にずれています
このdataを解析すると、

We simulate your bowling score in each scoring system
Original Score System:your average is:200   median is :200.0    variance is:649 stdev is:25.475478405713993
Current Score System:your average is:226    median is :226.0    variance is:600 stdev is:24.49489742783178
Current score is 26 pin higher than Original score in each game!!

となり、Currentの方が点数が高く出る上に、ばらつき(=分散) も小さいということが判明しました.
OriginalのAverageも記録を取っている2018のデータとほぼ一致しているので正しいと言えそうです.

筆者の場合 (初級者)

しかし、これだけでは満足せず　さまざまなレベルのボウラーでもCurrentは高く評価されるのかを検証するために、筆者がボウリングを始めて2年目の時のアプリの記録が残っていたのでその時の記録を元にモデルを作成しました.

def my_bowling_2():
    frame = 1
    a = []
    while frame <= 10:
        pinfall = np.random.choice([10, 9, 8, 7,6,5], p=[0.41, 0.25, 0.15, 0.12, 0.05, 0.02]) #my bowling data of 2018
        if pinfall == 10:
            a.append(pinfall)
            frame += 1
        if pinfall == 9 :
            spare = np.random.choice(2,p=[0.24, 0.76])
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 8:
            spare = np.random.choice(3,p=[0.16, 0.28, 0.56])
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 7:
            spare = np.random.choice(4 ,p=[0.09,0.12 ,0.32 ,0.47])
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 6:
            spare = np.random.choice(5 ,p=[0.05,0.06 ,0.25 ,0.29,0.35])
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 5:
            spare = np.random.choice(6 ,p=[0.03,0.13 ,0.13, 0.19 ,0.14,0.38])
            a.extend([pinfall,spare])
            frame += 1
    else:
        if a[-1] != 10: #bowler cannot strike in 1st shot at 10th frame.
            if a[-2] + a[-1] == 10: #bowler spares at 10 th frame, he can throw one more shot in original score system
                pinfall = np.random.choice([10, 9, 8, 7,6,5], p=[0.41, 0.25, 0.15, 0.12, 0.05, 0.02])
                a.append(pinfall)
        else: #bolwer strikes in 1st shot at10th frame ,he can throw 2 times in original score system
            pinfall = np.random.choice([10, 9, 8, 7,6,5], p=[0.41, 0.25, 0.15, 0.12, 0.05, 0.02])#my bowling data of 2018
            if pinfall == 10:
                pinfall_2 = np.random.choice([10, 9, 8, 7,6,5], p=[0.41, 0.25, 0.15, 0.12, 0.05, 0.02])#10th frame final shot
                a.extend([pinfall,pinfall_2])
            if pinfall == 9 :
                spare = np.random.choice(2,p=[0.24, 0.76])
                a.extend([pinfall,spare])
            if pinfall == 8:
                spare = np.random.choice(3,p=[0.16, 0.28, 0.56])
                a.extend([pinfall,spare])
            if pinfall == 7:
                spare = np.random.choice(4 ,p=[0.09,0.12 ,0.32 ,0.47])
                a.extend([pinfall,spare])
            if pinfall == 6:
                spare = np.random.choice(5 ,p=[0.05,0.06 ,0.25 ,0.29,0.35])
                a.extend([pinfall,spare])
            if pinfall == 5:
                spare = np.random.choice(6 ,p=[0.03,0.13 ,0.13, 0.19 ,0.14,0.38])
                a.extend([pinfall,spare])
    return a

これを同様に3000回投球させた時の結果が以下の図である.

このようにやはりずれている. どれぐらいずれているのかを算出すると、

We simulate your bowling score in each scoring system
Original Score System:your average is:181   median is :181.0    variance is:647 stdev is:25.436194683953808
Current Score System:your average is:206    median is :209.0    variance is:746 stdev is:27.313000567495326
Current score is 25pin higher than Original score in each game!!

するとどうでしょう、点数はやはり高くなりましたが、ばらつきが逆に多くなっています これはなかなかおもしろい結果です. つまり初心者はまぐれのスコアが出やすくなることがこのことから示唆されます.

上級者の場合

中級者、初級者ときたら　最後は上級者なのですが今回上級者として誰のデータを用いるかというと　ボウリング現ナショナルチーム で先月行われたアジア競技大会で日本人初の金メダルを獲得した 岡山商科大学4年生の　石本美来 さんに今回は協力していただいて modelを制作させていただきました.

石本美来さん(共同通信社から借用させていただきました)

石本さんの実績はこちらに載っております. ボウリング歴15年目で名実ともに日本のトップレベルのボウラーに今回はご協力いただいたことにここに感謝させていただきます.

さて、modelを実装してみました

def Ishimoto_bowling():
    frame = 1
    a = []
    while frame <= 10:
        pinfall = np.random.choice([10, 9, 8, 7,6,5], p=[0.60, 0.20, 0.10, 0.07, 0.02, 0.01]) #my bowling data of 2018
        if pinfall == 10:
            a.append(pinfall)
            frame += 1
        if pinfall == 9 :
            spare = np.random.choice(2,p=[0.05, 0.95])
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 8:
            spare = np.random.choice(3,p=[0.10, 0.10, 0.80])
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 7:
            spare = np.random.choice(4 ,p=[0.05,0.12 ,0.18 ,0.65])
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 6:
            spare = np.random.choice(5 ,p=[0.01,0.05 ,0.13 ,0.16,0.65])
            a.extend([pinfall,spare])
            frame += 1
        if pinfall == 5:
            spare = np.random.choice(6 ,p=[0.01,0.01 ,0.30, 0.43 ,0.05,0.20])
            a.extend([pinfall,spare])
            frame += 1
    else:
        if a[-1] != 10: #bowler cannot strike in 1st shot at 10th frame.
            if a[-2] + a[-1] == 10: #bowler spares at 10 th frame, he can throw one more shot in original score system
                pinfall = np.random.choice([10, 9, 8, 7,6,5],  p=[0.60, 0.20, 0.10, 0.07, 0.02, 0.01])
                a.append(pinfall)
        else: #bolwer strikes in 1st shot at10th frame ,he can throw 2 times in original score system
            pinfall = np.random.choice([10, 9, 8, 7,6,5], p= [0.60, 0.20, 0.10, 0.07, 0.02, 0.01]) #my bowling data of 2018
            if pinfall == 10:
                pinfall_2 = np.random.choice([10, 9, 8, 7,6,5],  p=[0.60, 0.20, 0.10, 0.07, 0.02, 0.01]) #10th frame final shot
                a.extend([pinfall,pinfall_2])
            if pinfall == 9 :
                spare = np.random.choice(2,p=[0.05, 0.95])
                a.extend([pinfall,spare])
            if pinfall == 8:
                spare = np.random.choice(3,p=[0.10, 0.10, 0.80])
                a.extend([pinfall,spare])
            if pinfall == 7:
                spare = np.random.choice(4 ,p=[0.05,0.12 ,0.18 ,0.65])
                a.extend([pinfall,spare])
            if pinfall == 6:
                spare = np.random.choice(5 ,p=[0.01,0.05 ,0.13 ,0.16,0.65])
                a.extend([pinfall,spare])
            if pinfall == 5:
                spare = np.random.choice(6 ,p=[0.01,0.01 ,0.30, 0.43 ,0.05,0.20])
                a.extend([pinfall,spare])
    return a

特筆すべきはカバー率の高さ、これが彼女の強さといっても過言ではありません.
さて、このmodelを3000回まわしてみました.

すると奇妙な形になりました.　
これはおそらくCurrentになったおかげで 290台が原理上出すのが困難になった. 一投目のカウントが良いのでスコアの1の位にバイアスがかかる. などが考えられると思います.
いずれにしろものすごく偏ったスコアメイクなっています.

実際に解析してみると、

We simulate your bowling score in each scoring system
Original Score System:your average is:223   median is :224.0    variance is:614 stdev is:24.779023386727733
Current Score System:your average is:247    median is :251.0    variance is:456 stdev is:21.354156504062622
Current score is 24 pin higher than Original score in each game!!

となりました. するとどうでしょう元々のアベレージが高いこともありますが、こんな上級者でも20数ピン上がることがわかりました. しかしレベルが上がるにつれてばらつきは小さくなっていることもこの結果から伺えます

Discussion & Conclusion

今回3つのボウラーのレベルでCurrent と Originalでどの程度スコアが上がるのかをシミュレーションしてみました.
計算させてわかったことは、

1.どんなレベルのボウラーでも20ピンは上がる
2.レベルが上がるにつれてCurrentのスコアのばらつきが小さくなる

ことが判明しました. Currentは点数が出やすいってことですね. ただ上手くなるとスコアはブレないよ　ということを計算機が教えてくれました...(練習します...)

Future Work

さすがに $n=3$　で有意！とするのは無茶なのはわかっていますが　本当に差が出るのか？を定式化したいと思っています.(ただ仮定をどうおくのかが重要だとは思いますが...)

Current と Original でスコアの紐付けができないか. いわば CurrentがOriginalの関数になっているのではないか、という仮定からOriginalの結果からCurrentを予測することはできないか？ (制限がないと過学習になりそうなので何かしらの制約は必要そうですが)

Current のスコアと Originalのスコアで相関が見られないか？　大規模な実データを必要とするかも.

訂正やコメントなどは随時受け付けています