- 本記事はProjectEulerの「100番以下の問題の説明は記載可能」という規定に基づいて回答のヒントが書かれていますので、自分である程度考えてみてから読まれることをお勧めします。
問題 68. 魔法5角リング
原文 Problem 68: Magic 5-gon ring
問題の要約 図 1のような図形のマルに1~10の数字を入れで以下の条件を満たすもので答えの16桁が最大になるものを求めよ
- 直線の3個のマルの数字の合計はすべて同じ
- 答えは、それぞれの3個の数字を外側から並べ、それをさらに外側の数の一番小さい数のものから時計回りに列挙したもので答えを表す。例えば図 2の3角魔法リングでは432:621:513となり、これが最大となる。
【図 1】
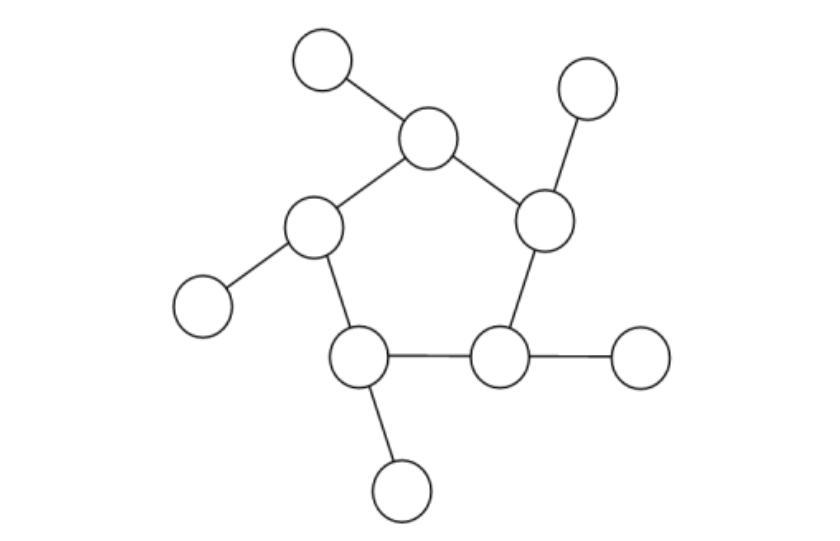
【図 2】

問題の考え方
なかなか、ややこしい問題なのでステップを踏んで考えて行きたいと思います。
- 5角魔法リングでは二けたの10が含まれ、これが内側のリングにあると答えに2回現れるので17桁になってします。したがって10は外側にある。
- 答えの16桁の最も大きい桁の数は外のリングの最小値、これを最大にするためには10以外の大きい数字「6,7,8,9」が外のリングに来て6が16桁の最初の数になる。
- その6からなる3つの数の2番目が答えの16桁の2桁目になるので、内のリングの最大値5を選びます。
- 外のリングが「6,7,8,9,10」、内のリングが「1,2,3,4,5」とすると16桁の合計は内のリングは2回登場するので(6+7+8+9+10)+2*(1+2+3+4+5)=70。したがって3つの数の和は14になる。
- 6からなる3つの数の3つ目は14-6-5=3。すると内のリングの残りの3つは「1,3,4」
- 内のリングの各辺の和は{4,5,6,7,8}にならなければならないので、「5,3,1,4,2」が来まり、外のリング「6,10,9,8,7」も来まる。
- これを答えの16桁にすると653:1031:914:842:725になる。
というように解いていくとプログラムを書かなくても紙と鉛筆で答えが出せてしまいました。