【Project Euler】Problem 82: 経路の最小値（３方向）

• 本記事はProjectEulerの「100番以下の問題の説明は記載可能」という規定に基づいて回答のヒントが書かれていますので、自分である程度考えてみてから読まれることをお勧めします。

問題 82. Path sum: three ways（３方向）

原文 Problem 82: Path sum: three ways

問題の要約：問題81と同じマトリクスの左端のどれかの数から左端のどれかの数まで上、下、右の３方向の動きを使ってで到達したときの経路の数の最小値を求めよ

この5 x 5の例題では赤の経路で994が最小値となります。

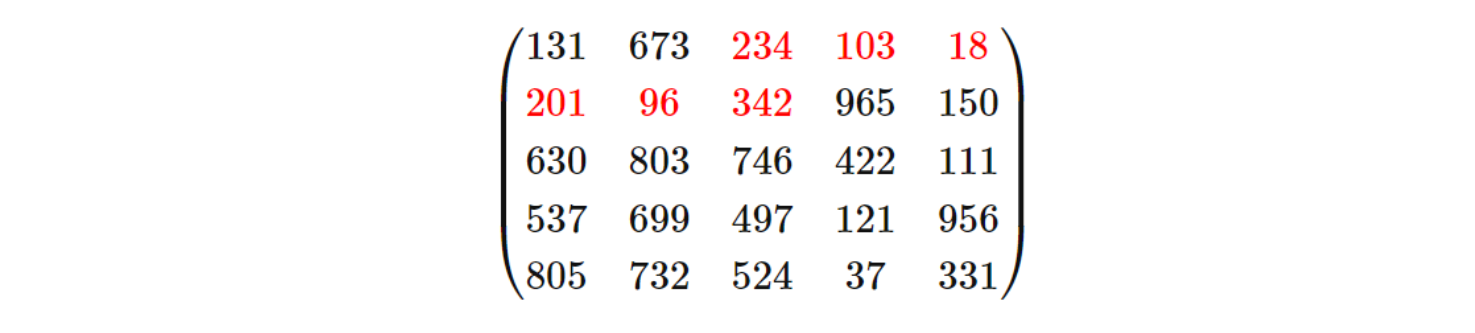
問題 81との違いは始点と終点が決まっていないことと、動きが3方向のことです。特に上と下は進行方向の右に進まない動きなので以下のように965から右の列に動くときに複数の動きを考慮する必要があります。

これを考慮すればあとは問題 81と同様に右から、右に一つ動く経路のなかの最小値を一つ左に足して行くことで最小値が求まり、最後の答えは左端の列の最小値となります。今回はマトリクスの部分を切り出すのが容易にできるようにnumpy.arrayを使いました。

import numpy as np
mtx = np.array(mtx)
for x in range(msize-2,-1,-1):
  mtx1 = np.array([0]*msize)
  for y in range(msize):
    mtx1[y] = min([ sum(mtx[y1:y:1 if y>=y1 else -1,x])+mtx[y1][x+1] for y1 in range(msize)]) 
  mtx[:,x] +=  mtx1   # add to orinal matrix (column x)
print(f"Answer: {min(mtx[:,0])}")

今回は始点と終点が決まっていないということでnetworkxは使いませんでした。

ファイルの読み込み

# show upload dialog

from google.colab import files
uploaded = files.upload()
#---- read numbers from file
f = open("p081_matrix.txt")
fmatrix = f.readlines()
f.close()
mtx = []
for l in fmatrix:
  l=l.strip()        #remove cr code
  mtx.append(list(map(int,l.split(",")  )))
msize = 80

（開発環境：Google Colab）