交差するはしご問題 (Crossed ladders problem)
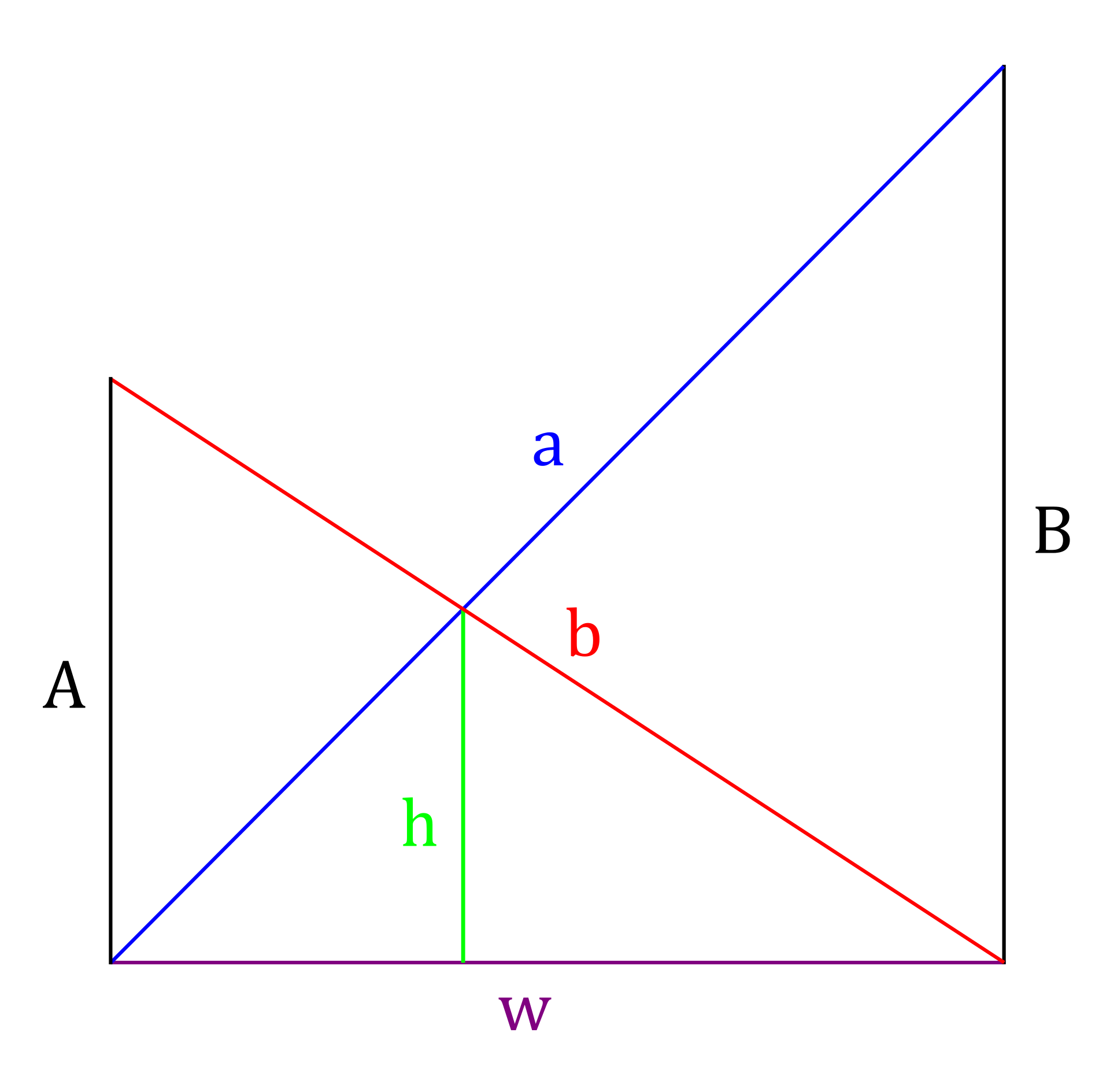
Wikipediaの英語版にあるCrossed ladders problemですが日本語訳がないので日本ではあまり馴染みのないかもしれません。幅がwで壁で挟まれた道路に長さがaとbのはしごをかけたときhを求めよという問題です。
この問題の整数解
Wolfram MathWorldにも同様の記事がありますがここにとても興味深い記述があります。変数の書き方が違いますが、要はすべての辺が整数になっているということです。今回はそれは他の例を探したいと思います。
これらの解の中に l_1, l_2, h_1, h_2, h だけでなく、d_1やd_2も整数となるものがあります。一つの例は(l_1,l_2,h_1,h_2,h,d_1,d_2)=(119,70,105,42,30,40,16)です。
【問題】 0<a<b<300 の時a, b, A, B, w, h, wa, wb (wをhの垂線で分割したもの) がすべて整数のものを、列挙せよ。
ステップ.1 ピタゴラス数
直角三角形で辺が整数ということで、
- 基本ピタゴラス数を発生させていきます。これについては参考コードがたくさんあると思いますので説明省略します。
- 基本ピタゴラス数を整数倍して三角形の長辺がN未満のものをすべて作ります。
- 直角を挟む2辺を片方をKeyにしてDICTに加えてリストにします。これによってwをしていしたとき、AとBの候補が分かります。例えばw=16の時は[12,30,63] が候補なのでここから2つ選ぶ組合せは[12,30], [30,63],[63,12]となるので、これをA,Bとして整数判定を行います。
コードは以下のようになります。
from collections import defaultdict
import itertools, math
## Generate Pythagorean triple
def pyth():
for m in itertools.count(2):
for n in range(1,m):
if (m%2)==(n%2): continue
if math.gcd(m,n) != 1: continue
yield m*m - n*n, 2*m*n, m*m + n*n
N = 300
ptall = defaultdict(list)
g = pyth()
for _ in range(N):
t = next(g)
for i in range(1,(N-1)//t[2]+1): # Multiples up to N
t1 = (t[0]*i,t[1]*i,t[2]*i)
for j in range(2): # Add to dict (both small edges)
ptall[t1[j]].append(t1[1-j])
print(len(ptall), ptall[16])
# 159 [12, 30, 63]
ステップ 2. hを求めて整数判定を行う
前出のWikiからhを求めるのは以下の式があります。hの整数判定を行った後、wa, wbを求めて整数判定を行えば完了です。
$\Large\frac{1}{A}+\frac{1}{B}=\frac{1}{h}$
$\Large h =\frac{A*B}{A+B} $
count = 0
for w in ptall.keys():
if len(ptall[w]) < 2: continue
for A, B in itertools.combinations(ptall[w],2):
if (A*B) % (A+B) == 0: # check h is integer
h = (A*B) // (A+B)
if w*h % A == 0 and w*h % B ==0: #check wa, wb are integers
wa, wb = w*h//A, w*h//B
a = int(math.sqrt(w**2+A**2))
b = int(math.sqrt(w**2+B**2))
count += 1
print(count, ":", a, b, A, B, h, w, wa, wb)
# 1 : 70 119 42 105 30 56 40 16
# 2 : 104 296 40 280 35 96 84 12
# 3 : 140 238 84 210 60 112 80 32
# 4 : 175 119 140 56 40 105 30 75
# 5 : 210 182 126 70 45 168 60 108
このコードを走らせると答のすべて整数となる組み合わせは5個あることが分かります。(1と3のように相似形のものを含んでいます)
ちなみにProject EulerのProblem 309: Integer Laddersはwa, wbが整数はもとめてないのでその判定を除いたものになります。