前回の問題が実はライプニッツの調和三角形と密接な関係があり、それを使って劇的なパフォーマンスの改善が行えることを示したいと思います。
ライプニッツの調和三角形
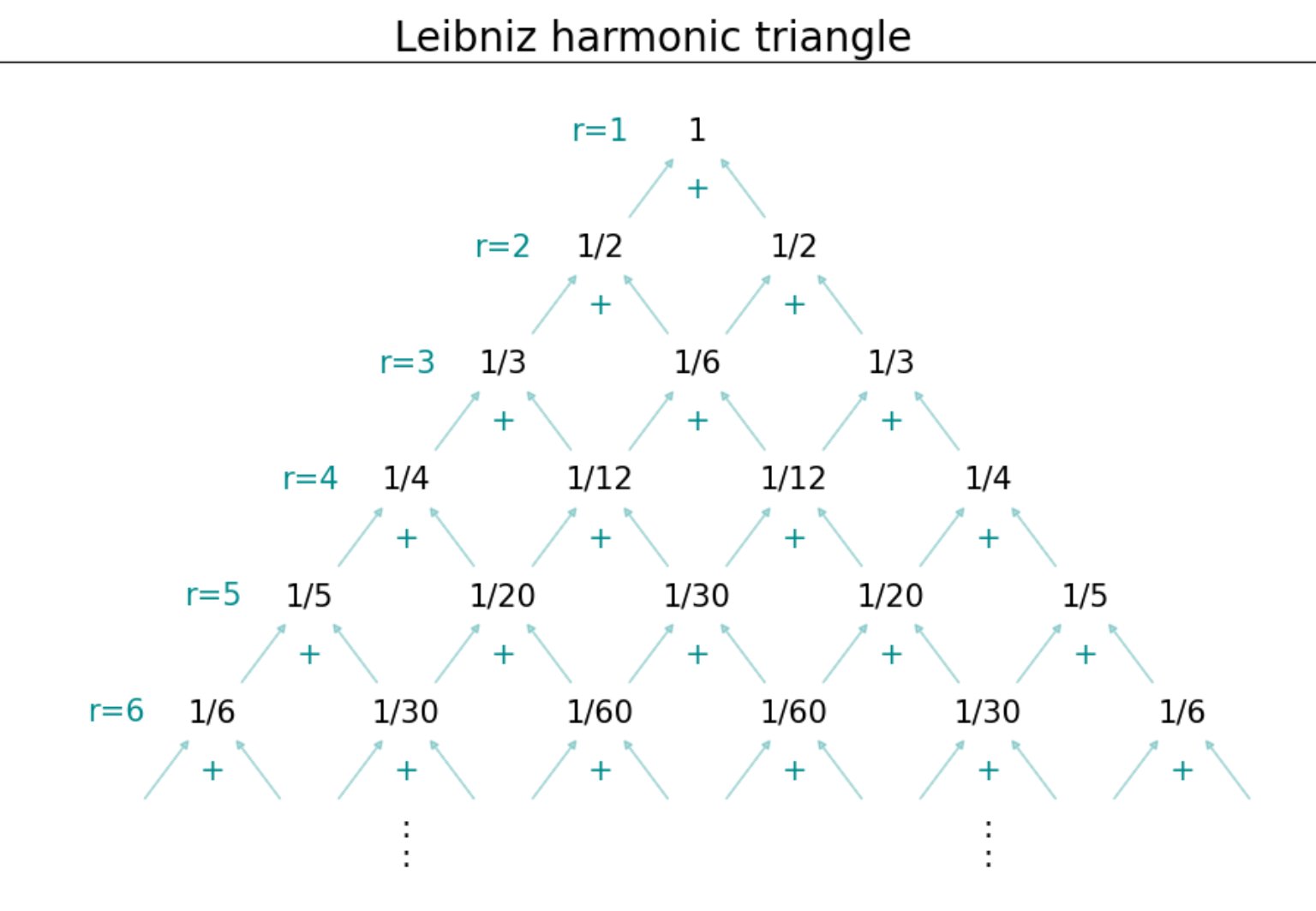
まずライプニッツの調和三角形 (Wikipedia)ですが。以下のルールで三角形を作ります。
- パスカルの三角形 (Wikipedia)と似た考え方
- $r$行目の両端は$1/r$
- パスカルの三角形とは逆に下の行の2つの数の和が上の行の数になる値をいれる
これを以下に図示します
例えば$r=3$の行は、第1列は$1/3$なので第2列は$1/2-1/3=1/6$というように求めて行きます。
調和三角形の一般項
この調和三角形の一般項はWikipediaによると以下となり、これは正しく前回の「各ターンの期待値」と同じ式になっています。
\begin{align}
L(r,c) &= \frac1{c \times \binom{r}{c}} \cdots (2-1) \\
& したがって \\
& E(n) = 調和三角形のr行目の和\\
\end{align}
調和三角形から漸化式を求める
4行目と5行目を比較して$E(n)$の漸化式を求めます
\begin{align}
E(4) &= 1/4 + 1/12 + 1/12 + 1/4 \\
& =(1/5+1/20) + (1/20+1/30) + (1/30+1/20) + (1/20+1/5) \\
& = 2 \times (1/5+1/20+1/30+1/2+1/5) - 2/5\\
& = 2 \times E(5) - 2/5 \\
& したがって \\
&E(5) = \frac1{2}E(4)+ \frac1{n}
\end{align}
\begin{align}
E(4) &= \frac1{4} + \frac1{12} + \frac1{12} + \frac1{4} \\
& =(\frac1{5}+\frac1{20}) + (\frac1{20}+\frac1{30}) + (\frac1{30}+\frac1{20}) + (\frac1{20}+\frac1{5}) \\
& = 2 \times (\frac1{5}+\frac1{20}+\frac1{30}+\frac1{20}+\frac1{5} - \frac{1}{5})\\
& = 2 \times( E(5) - \frac1{5}) \\
& したがって \\
&E(5) = \frac1{2}E(4)+ \frac1{n}
\end{align}
これはまさしく前回の式$(3)$です。あれだけ苦労して求めた式がこんなに簡単に求まってしまいました
調和三角形の面白い性質
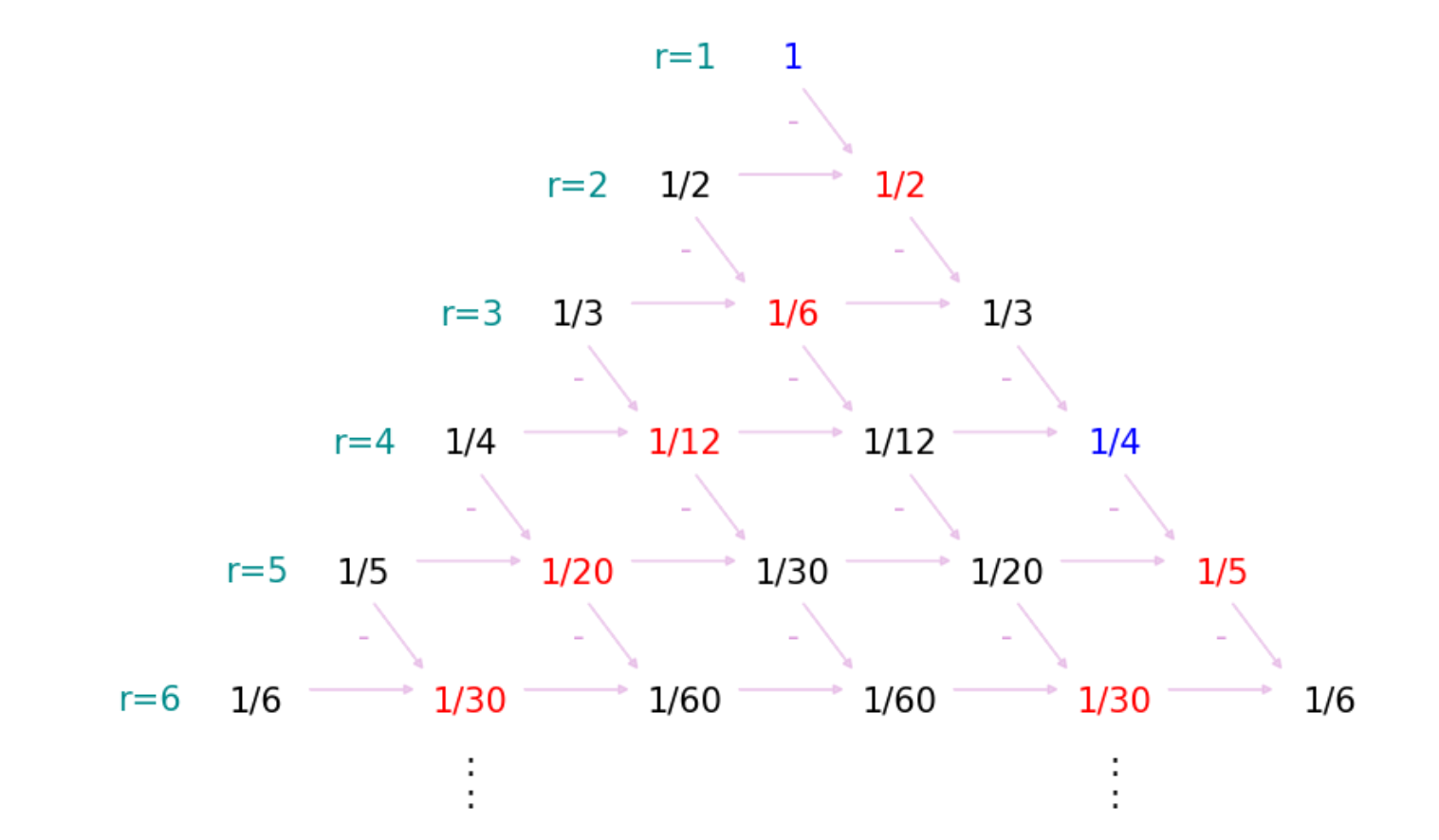
第2列を斜めに無限に足すことを考えます。するとそれは第1列の差で表されるので最初の1以外は消えて1となります。
\begin{align}
&= \frac1{2} + \frac1{6} + \frac1{12} + \frac1{20} + \frac1{30} +\cdots\\
& =(\frac1{1}-\frac1{2}) + (\frac1{2}-\frac1{3}) + (\frac1{3}-\frac1{4}) + (\frac1{4}-\frac1{5})+\cdots \\
&= 1 \\
\end{align}
同様に第5列の無限和は$1/4$となります。
\begin{align}
&= \frac1{5} + \frac1{30} +\cdots\\
& =(\frac1{4}-\frac1{20}) + (\frac1{20}-\frac1{60}) \cdots \\
&= 1/4 \\
\end{align}
それではすべての列の無限和は、
\begin{align}
第1列は& \frac1{1}+\frac1{2}+\frac1{3}+\frac1{4}+\cdots \\
第2列は& \frac1{1}\\
第3列は& \frac1{2}\\
& : \\
第r列は& \frac1{r-1}\\
&したがって \\
第2列以降の和も& \frac1{1}+\frac1{2}+\frac1{3}+\frac1{4}+\cdots \\
& よってライプニッツの調和三角形のすべての無限和は \\
& 2 \times (\frac1{1}+\frac1{2}+\frac1{3}+\frac1{4}+\cdots) \\
& 2 \times H(\infty)\\
\end{align}
ここで$H(n)$は調和級数 (Harmonic series)です。調和三角形$n$の和を$E(n)$とすると以下のように表されます。
\begin{align}\
\sum_{r=1}^{\infty}E(r)&= 2 \times H(\infty)\\
\end{align}
調和三角形のn行目までの和
それではn行目までの和はどうなるかというと、
\begin{align}\
\sum_{r=1}^{n}E(r)&= H(n)+\sum_{c=2}^{n}(\sum_{r=1}^{\infty}L(r,c)-\sum_{r=n+1}^{\infty}L(r,c))\\
調和三角形の&性質から \\
\sum_{c=2}^{n}\sum_{r=1}^{\infty}L(r,c)&= H(n)\\
同様にc列の&n+1行以降の無限和はL(n,c-1)と等しいので \\
\sum_{c=2}^{n}\sum_{r=n+1}^{\infty}L(r,c)&=\sum_{c=2}^{n+1}L(n,c-1)\\
& = \sum_{c=1}^{n}L(n,c) = E(n) \\
&したがって \\
\sum_{r=1}^{n}E(r) & = H(n) + H(n) - E(n)\\
& = 2H(n)-E(n) \cdots (2-2)\\
\end{align}
調和数列#発散率 (Wikipedia)によると、nが大きいときは
\begin{align}\
& H(n) \simeq \gamma + ln(n) + 1/2n \\
& \ \ \ ここで\gamma = 0.57721... (オイラー・マスケローニ定数 )\\
& さらに調和三角形の行の和は両端以外は無視できるので\\
& E(n) \simeq \frac{2}{n} \\
& \sum_{r=1}^{n}E(r) = 2 (\gamma + ln(n) + \frac1{2n}) - \frac{2}{n} \\
&= 2 (\gamma + ln(n)) - \frac1{n}\cdots (2-3)\\
\end{align}
これで本当に$S(N) = \sum_{n=1}^{N}E(n)$が求まるかを$N=10^{10}$で試してみます。
def H(n):
from numpy import euler_gamma
from math import log
return euler_gamma + log(n) + 0.5/n
n = 10**10
print(f"Answer = {2*H(n)-2/n:.010f}")
# Answer = 47.2061331896
これは(その1)で求めた値と小数点以下9桁まで一致しているのでかなりの精度だと言えると思います。この式だと$O(1)$なのでいくらでも$N$を大きくすることが出来ます。とりあえずこのままで$10^{100}$までは求まりました。
(開発環境:Google Colab)
この考え方はProject Euler, Problem 567, 568を解くのに役に立ちます。