【Project Euler】Problem 85: 長方形の数

• 本記事はProjectEulerの「100番以下の問題の説明は記載可能」という規定に基づいて回答のヒントが書かれていますので、自分である程度考えてみてから読まれることをお勧めします。

問題 85.長方形の数

原文 Problem 85: Counting rectangles

問題の要約：長方形の格子に置ける長方形の数を数えたとき、その数と$2*10^6$との差が最小になるような長方形の格子の面積を求めよ

この2x3の例では置ける長方形の数は合計18となります。

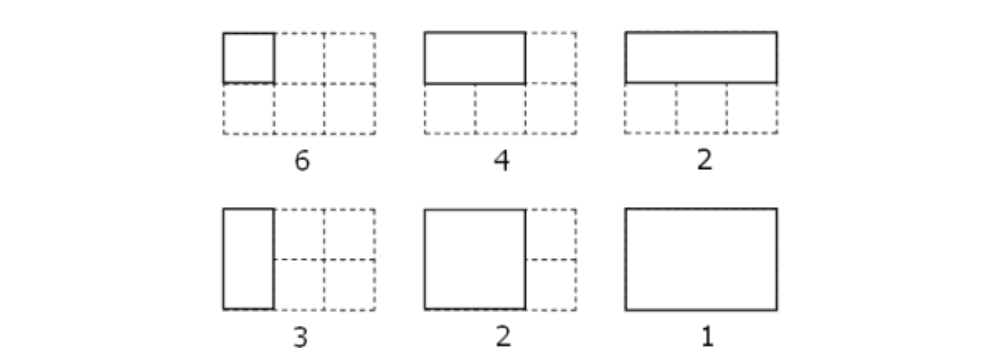
図をよく見ると、置ける数は右下らかの座標を$(x,y)$とすると$x \times y$となっていることが分かります。したがっておける長方形の数はその合計なので素直に実装するとこうなります。

import itertools
def countRect(xsize, ysize):
  return sum([x*y for x,y in itertools.product(range(1,xsize+1),range(1,ysize+1))])

Mil = 2*10**6
minDif = 100
for x,y in itertools.combinations(range(5,202),2):
    count = countRect(x, y)
    dif = abs(Mil - count)
    if dif < minDif:
      minDif, minArea = dif, x*y
print(f"Answer: {minArea}")

ここまで規則的だと和の式も出せそうなのでやってみます。

\large \sum_{x=1}^{X} \sum_{y=1}^{Y} x \times y \\
= \large \sum_{x=1}^{X} x \times  \sum_{y=1}^{Y}  y \\
= \large \frac{x(x+1)}{2} \times \frac{y(y+1)}{2} \\
= \large x(x+1)y(y+1)/4

ということでcountRectを以下のように書き換えるとかなり速くなります。

def countRect(x,y):
   return x*(x+1)*y*(y+1)//4

（開発環境：Google Colab）