【Project Euler】Problem 28: 数のらせんの対角線

• 本記事はProjectEulerの「100番以下の問題の説明は記載可能」という規定に基づいて回答のヒントが書かれていますので、自分である程度考えてみてから読まれることをお勧めします。

問題 28：数のらせんの対角線

原文 Problem 28: Number spiral diagonals

問題の要約：図のように1から順番にマスにらせん状に書いて行ったとき1001 x 1001のマスが埋まったときの対角線の数の合計を求めよ

なんとなく規則性はつかめそうに思えますが。まず規則通りにマスを埋めるプログラムを書いてみます。

import numpy as np
N = 9
vectors = np.array([[-1,0],[0,1],[1,0],[0,-1]]) # direction (0:up, 1:right, 2:down, 3:left )

matrix = np.array([0]*(N**2)).reshape(N,N)  # Fill 0s in N x N matrix 
pos = np.array([(N-1)//2, (N-1)//2])   # Start position

dir = 0      # direction index (0:up, 1:right, 2:down, 3:left )
for i in range(1,N**2+1):
  matrix[pos[0],pos[1]] = i         # put the number 
  rpos = pos + vectors[(dir+1)%4]
  if matrix[rpos[0],rpos[1]] == 0:  # if right pos is 0, then turn right
    dir = (dir+1)%4         # right direction
  pos = pos + vectors[dir]  # next position

print(matrix)

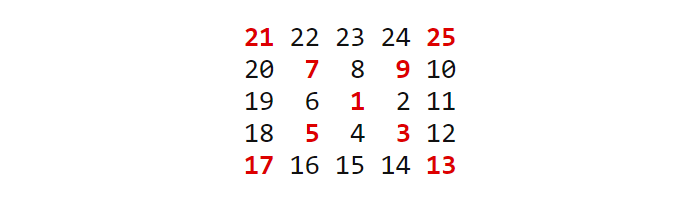
N=9でできたマス目を表示します。

[[73 74 75 76 77 78 79 80 81]
 [72 43 44 45 46 47 48 49 50]
 [71 42 21 22 23 24 25 26 51]
 [70 41 20  7  8  9 10 27 52]
 [69 40 19  6  1  2 11 28 53]
 [68 39 18  5  4  3 12 29 54]
 [67 38 17 16 15 14 13 30 55]
 [66 37 36 35 34 33 32 31 56]
 [65 64 63 62 61 60 59 58 57]]

これをじっと見ていると規則性が見えてきます。一辺の長さは2つづつ増えているので、間隔dで4つの角を数字求めて、dを2つ増やすのを繰り返せばいいですね。その合計が答えということです。

N = 9
dg = [1]
n, d = 1, 0
for i in range((N-1)//2):
  d += 2
  for i in range(4):
    n += d
    dg.append(n)
print(sum(dg), dg)
#537 [1, 3, 5, 7, 9, 13, 17, 21, 25, 31, 37, 43, 49, 57, 65, 73, 81]

（開発環境：Google Colab）