最短時間の経路をスネルの法則を使って求める

最短時間の経路問題

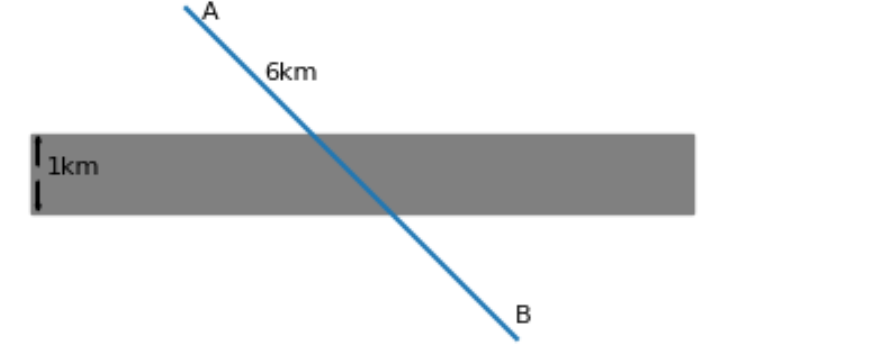
以下の図で6km離れたA点からB点に移動したいが、間に幅1km砂利が敷き詰められた場所がある。普通の道は時速6km/hで歩けるが砂利のところは4km/hになる。最短移動時間を求めよ.

この砂利が無ければ1時間で移動できますが。まっすぐ進んだ場合砂利の部分の長さは$w=\sqrt{2}$kmなので移動時間$t$は以下のようになります。これが経路を変えると短くなるのかという問題です。

t = (6-w)/6 + w/4 = 1.118

スネルの法則

以下のリンクを参考すると分かるようにスネルの法則は光の屈折率を求める公式ですが、その屈折率に沿った経路が最短時間となることが証明されています。

スネルの法則をフェルマーの原理を用いて証明

そこで以下のスネルの法則に基づいて境界で経路を曲げて最後にゴールのB点に到達するような"入射角"をBinary Searchで求めるようなプログラムを書きました。

入射前/後の速度を$v_1$/$v_2$とすると入射/出射角$t_1/t_2$の関係

\frac{\sin t_1}{\sin t_2} = \frac{v_1}{v_2} 

from math import sqrt, sin, asin, cos, pi, radians, degrees, tan
L = 6   # direct distance
W = 1   # marsh width
s = [6, 4, 6]  # Speed of walk in each strip
Xab  = L/sqrt(2)
w0 = (Xab-W)/2
w = [w0, W, w0]  # width of each strip

def refract(deg):  # return x-final position, travel time
  t1 = radians(deg)
  xsum, ttime = 0, 0 
  for i in range(len(s)):
    xsum += w[i]* tan(t1)          # x position accumulative
    ttime += (w[i]/cos(t1)) / s[i] # travel time
    if i == len(s)-1: break
    t1 = asin(s[i+1]*sin(t1)/s[i]) # next refraction angle
  return xsum, ttime

# Binary search to find target xsum from initial angle
d1, d2 = 45, 70   # 
while True:
  dc = (d1+d2)/2
  xsum, ttime = refract(dc)
  if abs(Xab-xsum) < 10**(-5): break  
  if xsum < Xab:
    d1 = dc
  else: 
    d2 = dc

print(f"Answer: {ttime:.03f}, angle = {dc:.1f}")
# Answer: 1.104, angle = 48.5

このように最初の入射角を48.5度にすることで移動時間が短縮されたことが分かります。

	最短移動時間	最初の入射角
砂利が無ければ	1時間	45度
砂利も含めてまっすぐ	1.118時間	45度
最短時間経路	1.104時間	48.5度

（開発環境：Google Colab）

この問題はProject Euler Problem 607: Marsh Crossingを解くのに役に立ちます。