ミンコフスキー和とは?
残念ながらWikipediaには日本語版が見つからなかったので(Minkowski addition(英語))によると以下のように定義されています。
幾何学でミンコフスキー和とは、2つの位置ベクトルの集合A、Bがあったとき、そのすべてのベクトルを互いに足し合わせた位置ベクトルの集合である。
A + B = \{a+b \space | \space a \in A, b \in B \}
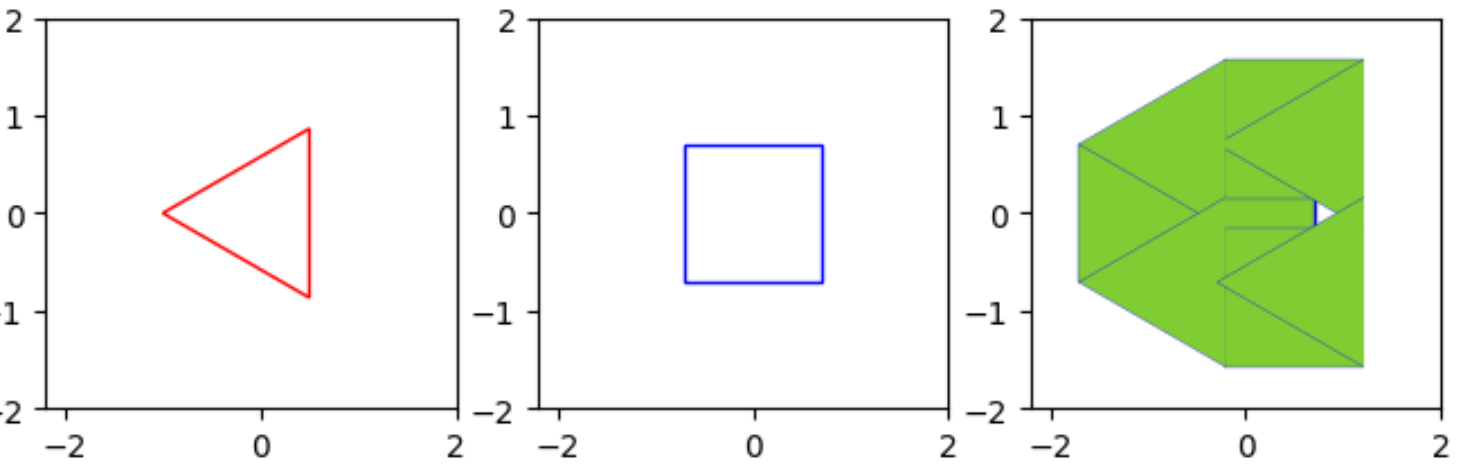
正3角形と正4角形のミンコフスキー和は?
例として正3角形と正4角形のミンコフスキー和は以下のように台形のような6角形になります。
なぜそうなるのかというと、一般にミンコフスキー和は図形2のある点を図形1の辺に沿って移動した跡となるからです。(図形2と1は逆でも良い)

ミンコフスキー和の図形の外枠を描く
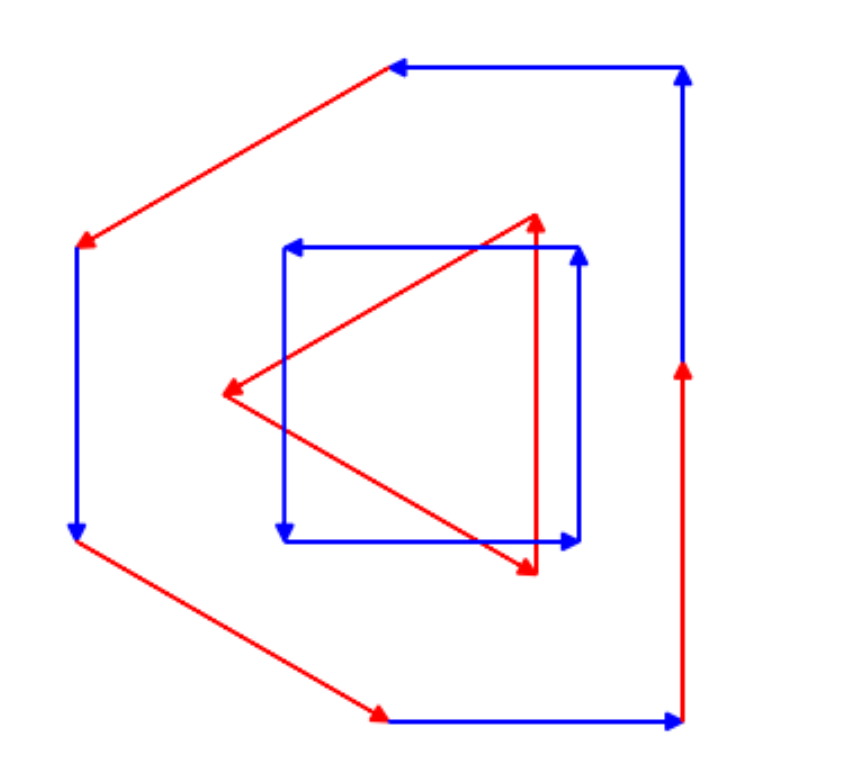
上記の方法で図形$A$をもう一つの図形$B$沿って移動させれば$A+B$の図形の形は分かりますが。もっとすっきりと外枠だけを書きたいです。そこでWikipediaのTwo convex polygons in the planeの項を見ると、
両方とも凸の$m$角形$A$と$n$角形$B$の辺が各々ベクトルのリストで表されているとき、$A+B$の辺は、ベクトルのリストをマージしてその偏角でソートして描いたものになる(要約)。
ということなのでその通りに描いてみると、期待通り同じ6角形の図形になりました。分かりやすいようにどちらの辺を使ったかを色で表してあります。すべての辺がもれなく使われているのが分かります。(これを描くpythonのコードは最後に添付しました)
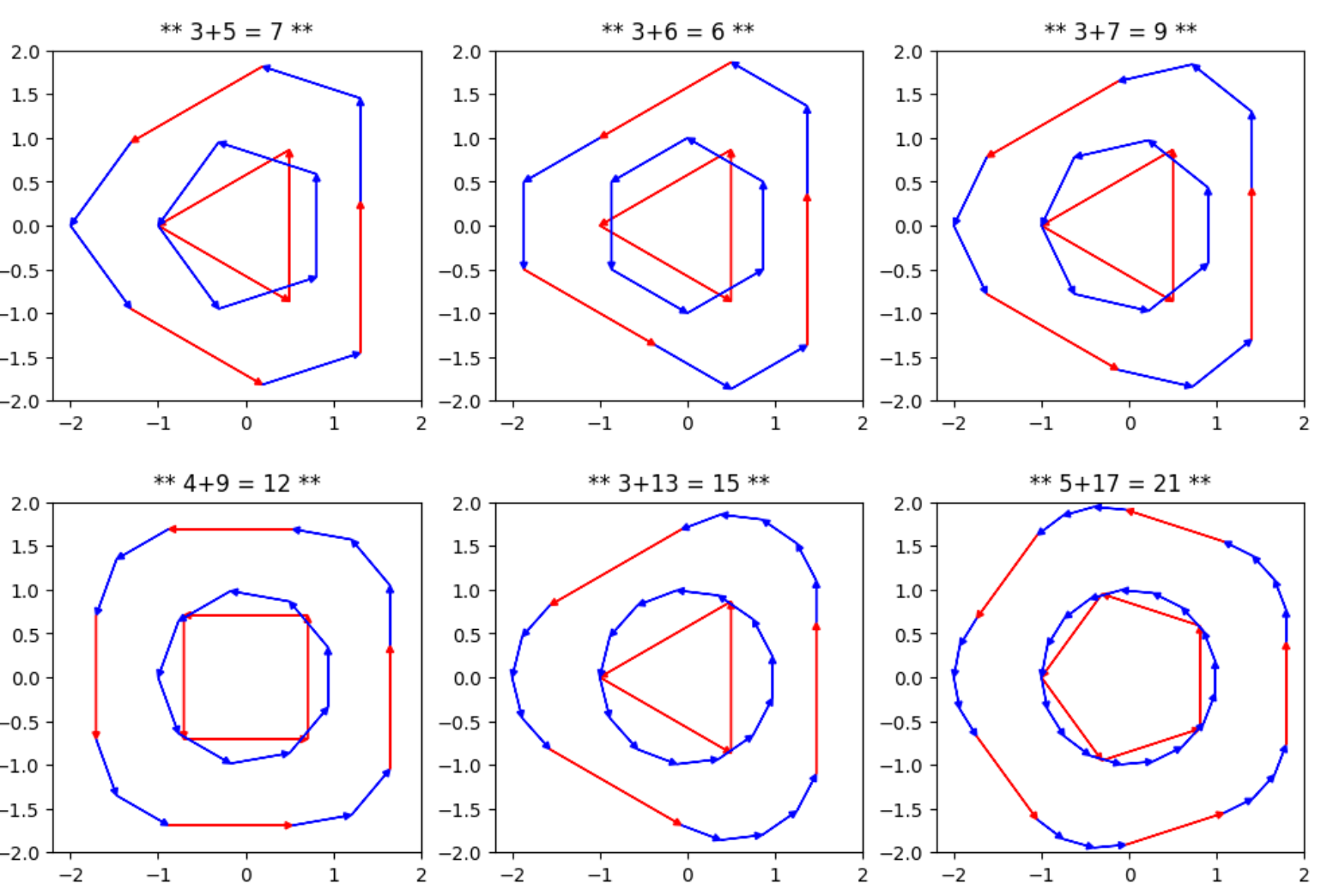
色々な正多角形の組合せのミンコフスキー和
このコードを使って色々な正多角形の組合せのミンコフスキー和を描いてみました。
m角形とn角形のミンコフスキー和は何角形になるか?
これらの結果を見ると何角形になるかは想像できると思います。最大は(m+n)角形ですが元の図形通しに平行な辺があると、その数だけ辺の数が減ります。
したがって以下のように表せます。
(ミンコフスキー和の多角形の辺の数) = m+n - (平行な辺の数)
例えば上の図の"3+6"のケースでは(平行な辺の数)=3なので、
(ミンコフスキー和の多角形の辺の数) = 3+6-3 = 6
となります。
ミンコフスキー和の図形の外枠を描くPythonのコード
import matplotlib.pyplot as plt
import cmath
# Create vectors of n-polygon edges (vt[0]=initial position)
def polygvtl(n, cid):
vt = [cmath.rect(1, cmath.pi*(2*k-1)/n) for k in range(1,n+1) ]
return [(vt[0], cid)]+[(vt[(i+1)%len(vt)]-vt[i],cid) for i in range(len(vt))]
#----- Draw vectors --------
# vtl: [(stv, cid0),(v1, cid1),(v2, cid2),...]
def drawvector(ax, vtl):
def c2xy(c): # convert complex to x,y coordinate
return (c.real, c.imag)
st, cid = vtl[0] # Initial point
for vt, cid in vtl[1:]:
stxy, vtxy = c2xy(st), c2xy(vt)
col = ['red', 'blue'][cid] # arrow color
ax.arrow(stxy[0], stxy[1], vtxy[0], vtxy[1],
head_width=0.08, head_length=0.08,
length_includes_head=True, fc=col, ec=col)
st = st+vt
#---- Minkowski Sums of two convex polygons -----
def MinkSum(p1, p2): # union of all edge vector
def pol(z):
ret = cmath.polar(z[0])[1]-cmath.pi*0.500001 # rotate -90
return ret if ret > 0 else ret+cmath.pi*2
sp = [(p1[0][0]+p2[0][0], 0)] # initial point
return sp+sorted(p1[1:]+p2[1:], key=lambda z: pol(z))
#---- Create matplotlib subplots ----------
fig, ax = plt.subplots()
ax.set_xlim(-2.2, 2.2)
ax.set_ylim(-2.0, 2.0)
ax.set_aspect('equal')
v1, v2 = 3,4
vtl1, vtl2 = polygvtl(v1, 0), polygvtl(v2, 1)
drawvector(ax, vtl1) # Draw polygon1 (red)
drawvector(ax, vtl2) # Draw polygon2 (blue)
drawvector(ax, MinkSum(vtl1, vtl2)) # Minkowski Sum
plt.show()
(開発環境:Google Colab)
この考え方はProject Euler Problem 228: Minkowski Sumsを解くのに役に立ちます。