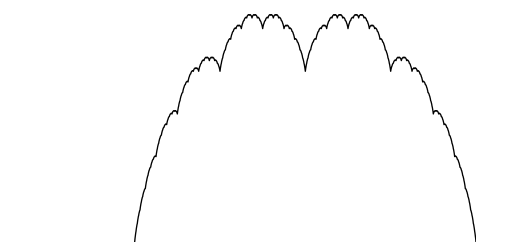
ブラマンジェ曲線
ブラマンジェ曲線は高木曲線(Wikipedia)とも呼ばれる中点を再帰的に分割してできるフラクタル曲線の一種とのこと。
その定義は以下のようにかなり難しい式で表されるますが、
\large T(x) = \sum_{n=0}^{\infty} \frac{s(2^nx)}{2^n} \\
ここで \large s(x)=min_{n \in Z}|x-n|
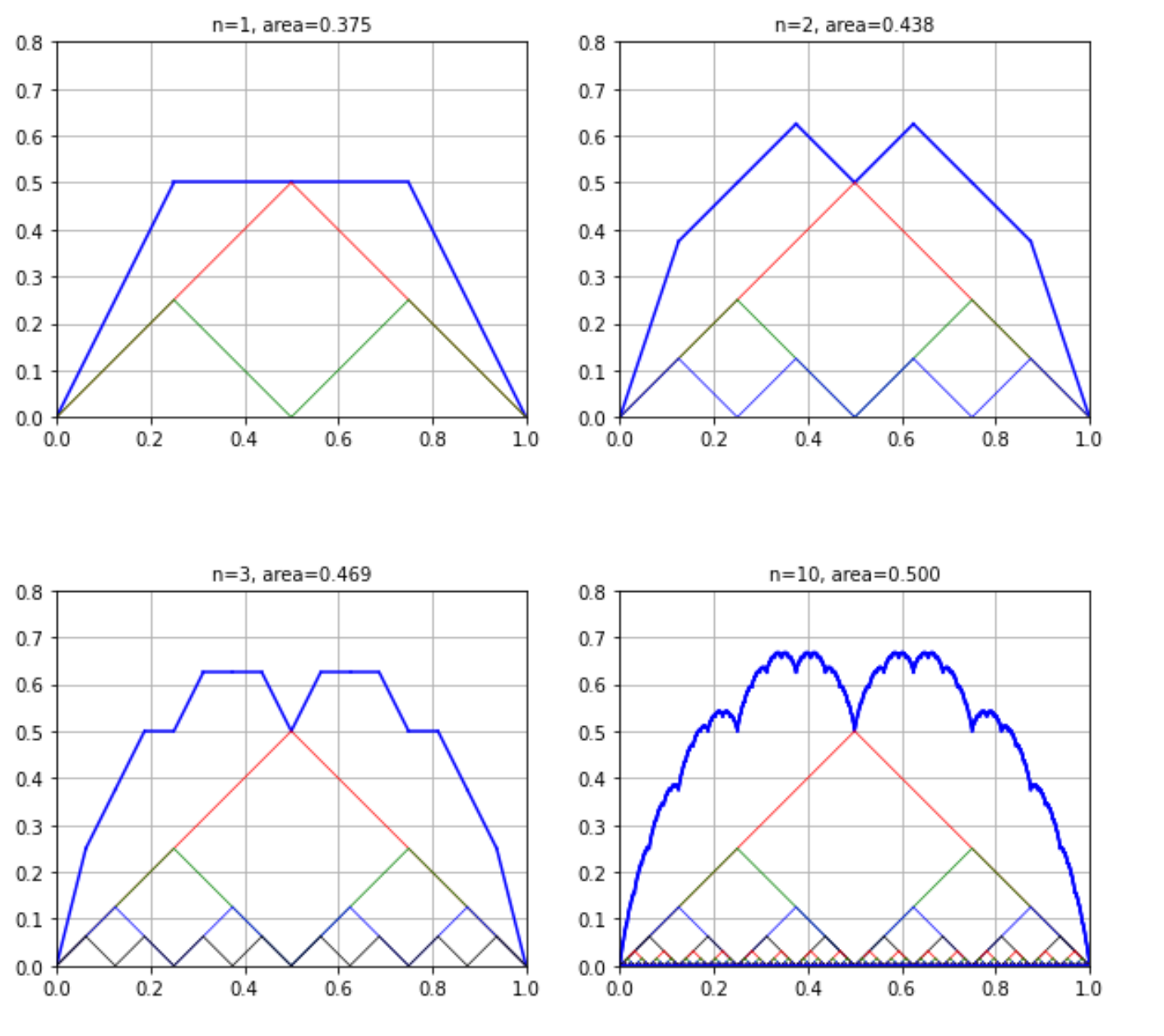
Wikipediaにもあるように三角波関数を波長・高さを半分にしていき足し合わせることで近似値を得ることが出来ます。n=1,2,4,10の結果を図にすると以下のようになります。
ブラマンジェ曲線の面積
そこでこのブラマンジェ曲線とX=0に囲まれた部分の面積です。三角波関数の面積が1/2の等比数列になっていることから0.5になりそうなことは容易に想像できまが、実際にプログラムで求めてみます。プログラムは三角波関数を再帰呼び出しで実装しています。
# ブラマンジェ曲線の面積
def blan(x1, dx, y1, y2):
dx1, y0 = dx/2, (y1+y2)/2
if dx <= TH:
return dx * y0
ret = blan(x1, dx1, y1, y0+dx1) + blan(x1+dx1, dx1, y0+dx1, y2)
return ret
TH = 1/(2**10)
area = blan(0, 1.0, 0, 0.0) # x1, dx, y1, y2
print(f"Answer = {area:0.3f}")
# Answer = 0.500
となり予想どおりの結果が得られました。
このアルゴリズムはEuler Project: Problem 226に役に立ちます。
(開発環境:Google Colab)