前置き
SPHに関する解説は様々な人が書いていますが、NiagaraのSimulationStageで実装するにあたって調べたことを、私もまとめてみることにしました。
他の人に共有する事もそうですが、どちらかというとまとめる過程で知識の整理ができることを狙っています。
自分の理解が怪しいと、他の人には伝えられませんからね。
SPH法について
概要はWikipediaを参照
流体計算を有限個の粒子で近似し、粒子を移動させながら解析する粒子法。といってもよく分からないと思います。
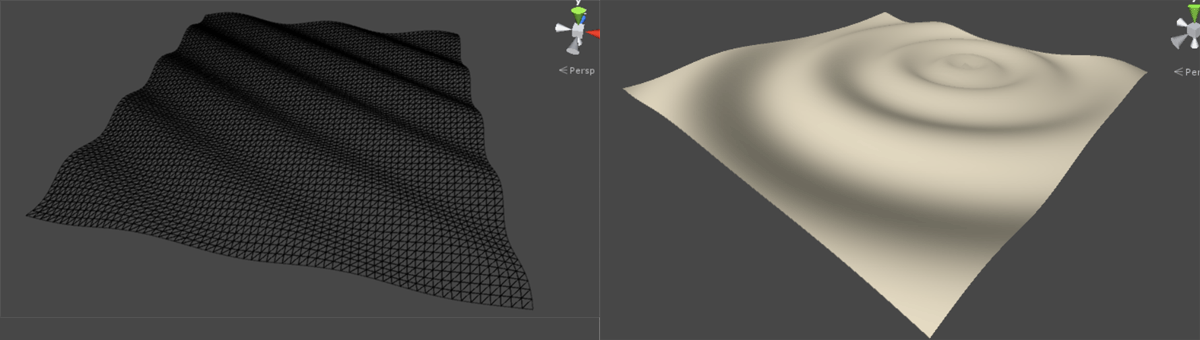
今でも簡易的な海などの表現に使われるメッシュ法は
(引用:http://marupeke296.com/Shader_No8_GeoVtxOperation.html)
このようにグリッドメッシュを動かして波などを表現していました。
一方SPHで使われている粒子法は、

(引用:https://www.youtube.com/watch?v=-cKgZrrBJ2w / ![]() は追記)
は追記)
メッシュの形状には縛られず粒子単位で管理しているので、このように水面から離れた状況もシミュレートできます。
SPH法の説明
さて、粒子法がどんなものか分かったところで、SPHの式見てみましょう。
Navier-Stokes(ナビエ・ストークス)方程式というものを使います。
\frac{Dv}{Dt}=-\frac{1}{\rho}\nabla p+\nu\Delta v+g
初見だと、これだけでもおなか一杯になりそうですが、元のNavier-Stokes方程式はもっと複雑で、非圧縮性(密度が一定)かつ粘性率が一定と仮定することでこの式まで単純化しています。
$\nabla$(ナブラ)と$\Delta$(ラプラシアン)について
ナブラと言ったら高速ナブラ!という古ゲーマーは多いと思いますw
話を戻して、詳細な定義からするとずれているかもしれませんが、今回の場合は空間(ベクトル場)に対して$\nabla$は一階微分、$\Delta$は二階微分を表しています。実際に$\Delta$は「$\nabla^2$」や「$\nabla \cdot \nabla$」と表現されることもあります。
身近(?)な例だと、微分の対象が空間ではなく時間ですが、位置、速度、加速度の関係がそれにあたります。位置の変化を時間で微分すると速度になりますし、速度の変化をさらに時間で微分すると加速度になります。
$ \hspace{100pt}v=\frac{dx}{dt},\ a=\frac{dv}{dt}=\frac{d^2x}{{dt}^2}$
さて、Navier-Stokes方程式の詳細を見ていきます。
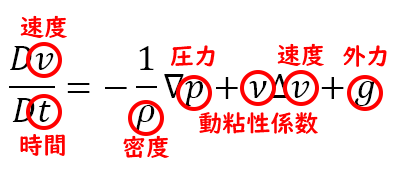
ついさっき出てきたような形もありますね。動粘性係数の$\nu$(ニュー)と速度の$v$(ブイ)、密度の$\rho$(ロー)と圧力の$p$(ピー)はそれぞれ似ているので、注意してみてください。とまぁ、細かく見るとこんな感じで要素が一杯なんですが、大きく分けるとこんな感じになります。

要は、粒子の加速度は圧力項と粘性項、外力(≒重力)を足すと求まります。ってことを表しています。
離散化
このままでは、プログラムで計算できないので離散化します。扱いやすいように式を変形し、各項を分離しておきます。
\begin{align}
& \frac{Dv}{Dt}=\frac{1}{\rho}\left(-\nabla p+\mu \Delta v+ \rho g\right)\hspace{50pt}\\
& \frac{Dv}{Dt}=\frac{1}{\rho}\left(圧力項+粘性項+外力項\right)\\
& 圧力項=-\nabla p\\
& 粘性項=\mu \Delta v\\
& 外力項=\rho g
\end{align}
粘性項の$\nu$(動粘性係数)が$\mu$(粘性係数)に置き換わっていますが、以下の関係にあります。
\nu=\frac{\mu}{\rho}\\
\left\{
\begin{array}{ll}
\nu=動粘性係数(\mathrm{m^2/s})\\
\mu=粘性係数(\mathrm{Pa \cdot s})\\
\rho=密度(\mathrm{kg/m^3})
\end{array}
\right.
単位変換
ここで出てきたそれぞれの単位、ぱっと見変換できなさそうですが、定義を紐解いていくとちゃんと=で結ばれます。
SI単位の定義によると、
$\hspace{100pt}Pa=\frac{N}{m^2},\ N=\frac{kg \cdot m}{s^2}$
となっています。これを踏まえて各単位を全部並べると
$\hspace{100pt}\frac{m^2}{s}=\frac{kg \cdot m \cdot s \cdot m^3}{s^2 \cdot m^2 \cdot kg}$
となって、ちゃんと=で結ばれます。
続けて、各粒子に対する加速度($a_i$)を求めるために、$\nabla$(空間微分)を離散化します。
a_i=\frac{1}{\rho_i}圧力項_i+粘性項_i+外力項_i\\
圧力項_i=-\sum_{j}m_j\frac{p_j}{\rho_j}\nabla W(x_i-x_j)\\
粘性項_i=\mu \sum_{j}m_j \frac{v_j}{\rho_j}\Delta W(x_i-x_j)
となります。ここで、$m_j$は各粒子の質量、$\nabla W(x_i-x_j)$などは重み関数(後述)です。
ただ、この式だとニュートン力学における第三法則の「作用反作用の法則」を満たしていない為、ダメだそうです。という事で圧力は平均を取り、速度は差分を取ることで作用反作用の法則を満たすように対称化を行います。
圧力項_i=-\sum_{j}m_j\frac{p_i+p_j}{2\rho_j}\nabla W(x_i-x_j)\\
粘性項_i=\mu \sum_{j}m_j\frac{v_j-v_i}{\rho_j}\Delta W(x_i-x_j)
密度_ρ_
未知の変数の導出を進めます。次は密度$\rho$です。
\rho_i=\sum_{j}{m_jW(x_i-x_j)}
意外と単純で、近傍粒子の質量を重み係数に従ってかき集めるだけです。
圧力_p_
次に圧力$p$を求めます。SPH法では理想気体の状態方程式を使って圧力を求めます。
p_i=k(\rho_i-\rho_0)
ここで、$k$は気体定数、$\rho_0$は静止密度(安定状態の基準密度)です。密度が基準密度より高いと圧力が上がるという式になっています。
この式だと水の様な非圧縮流体は扱えないらしいですが、そこは係数$k$で何とかします。また、密度の低い境界面で負圧が発生し、粒子が集まりすぎてしまうので、圧力$p_i$が負の時は$p_i=0$とします。
SPH重み関数
ここまでで三種類の重み関数が出てきました。基本的にどれも__良い感じに近似する為の関数__という扱いの様です。もちろん、導出の根拠はあると思いますが、長くなりそうなので結果だけ順にみていきましょう。
まずは、密度計算に出てきた重み関数
\begin{align}
& W(x_i-x_j)=\\
& W_{poly6}(r)=c\left(h^2-|r|^2\right)^3\\
& c=\begin{cases}
\frac{315}{64\pi h^9} &(3D)\\
\frac{4}{\pi h^8} &(2D)\\
0 &(|r|>h)
\end{cases}
\end{align}
次に圧力項に出てきた重み関数
\begin{align}
& \nabla W(x_i-x_j)=\\
& \nabla W_{spiky}(r)=c\left(h-|r|\right)^2\frac{r}{|r|}\\
& c=\begin{cases}
-\frac{45}{\pi h^6} &(3D)\\
-\frac{30}{\pi h^5} &(2D)\\
0 &(|r|>h)
\end{cases}
\end{align}
最後に粘性項に出てきた重み関数
\begin{align}
& \Delta W(x_i-x_j)=\\
& \Delta W_{visc}(r)=c(h-|r|)\\
& c=\begin{cases}
\frac{45}{\pi h^6} &(3D)\\
\frac{20}{3\pi h^5} &(2D)\\
0 &(|r|>h)
\end{cases}
\end{align}
ここで、$r$は粒子間の距離、$h$は粒子間の力が及ぶ範囲です。
どれも似たような式ですが微妙に違います。共通しているのは$|r|>h$、つまり粒子間の距離が影響範囲外なら0になるという点です。
また、2Dと3Dで係数が異なっているので、実装している次元に合わせて選択してください。
計算量を減らすために
何も考えずに実装を進めると、ある粒子を計算するのに、ワールドに存在する他の粒子全ての情報を参照しに行く必要が出てきます。しかし
$|r|>h$、つまり粒子間の距離が影響範囲外なら0になる
という条件があるので、実際には影響範囲より外側の粒子に関しては計算する必要がありません。
そこでよく使われるのが、空間上に位置によって粒子をグループ化しておき、ある粒子を計算する時は、近い粒子の情報だけを参照しやすくするデータ構造を採用する事です。
具体的な実装の仕方は色々ありますが、UE4のNiagaraではNeighborGrid3DというData Interfaceでそれが実現されています。
まとめ
ここまでで説明した内容で、未知の変数は無くなりました。振り返って、この計算で求められるのは

のとおり、加速度です。という事は、差分時間Δtを使って、シミュレーション結果の位置を求められます。
{v_i}(t+\Delta t)={v_i}(t)+\Delta t\cdot a_i\\
{P_i}(t+\Delta t)={P_i}(t)+\Delta t\cdot v_i
あとは、粛々とNiagaraのSimulationStageで実装するだけです!(それも大変ですが)
Appendix: 参考資料
SPH法による流体シミュレーションについて
SPHについて、実装を踏まえた一番わかりやすい解説でした。(圧力項の部分だけちょっと間違えている気がしてますが…)
粒子法:SPH法での物理量の近似
SPHについて、より理論を掘り下げたい場合はこちらの記事が参考になります。
SPH法について
SPHの式変形についての補足資料として
SPH法の重み関数
今回採用した重み関数は計算量なども考慮して、選択されていますが、それ以外の種類も掲載されています。
最後の方には導出方法も書かれています。
粘性係数と動粘性係数
粘性係数の変換についての解説です
初学者のためのナブラ演算子を用いた「勾配grad」「発散div」「回転rot」
∇(ナブラ)について易しめの解説