【初学者向け】暗号基本技術まとめ その2 ～共通鍵暗号/公開鍵暗号～

目的

前回からもう一歩踏み込んで、共通鍵暗号、公開鍵暗号の詳細を学ぶ

目次

• その1：暗号技術で重要な役割を果たす基本要素について学ぶ
• 【今回】その2：共通鍵暗号、公開鍵暗号(DES、AES、RSA、楕円曲線暗号など)の詳細を学ぶ
• (予定)その3：デジタル署名、証明書の詳細を学ぶ
• (予定)その4：opensslなどを使った実践

勉強メモ

共通鍵暗号と公開鍵暗号の比較

暗号処理のイメージ図

共通鍵暗号の場合(例：DES暗号/ECBモード)

公開鍵暗号(例：RSA暗号)

共通鍵暗号

※共通鍵暗号ってどんなもの？という方は前回の記事をご覧ください。

歴史的な背景

技術の話に入る前に少し、共通鍵暗号の技術遍歴に触れておく。¹

• DES(Data Encryption Standard)が現代の共通鍵暗号の始まりと言われている
• しかし、DESはコンピューター処理速度向上に伴い、現在ではブルートフォースアタックで解読できるようになってしまった
• NIST(National Institute of Standards and Technology：米国国立標準技術研究所)からも現在は利用を推奨しないという扱いになっている
• DESに代わる新しい共通鍵暗号の標準として選定されたのがAES(Advanced Encryption Standard)で、現在でもよく利用されている

DES

概要

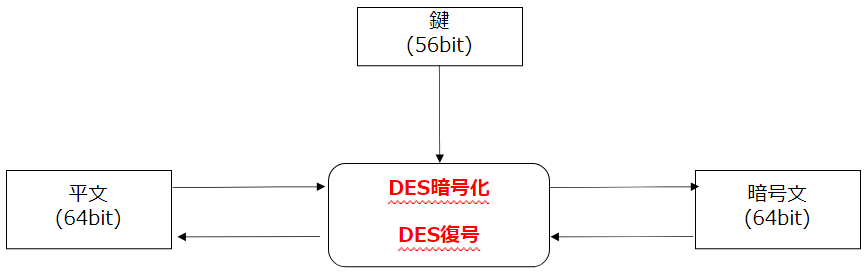
• ブロック暗号アルゴリズムの一種
• 暗号化/復号が同じ構成で実現可能 = 対称暗号の性質
• 鍵長：56bit、ブロック長：64bit(鍵長は64bitだが7bitごとに1bitのエラー訂正情報が入るため実質56bit)​
• 64bit以上の平文の暗号化は繰り返しの暗号化が必要(この繰り返し方法をモードという)

トリプルDES

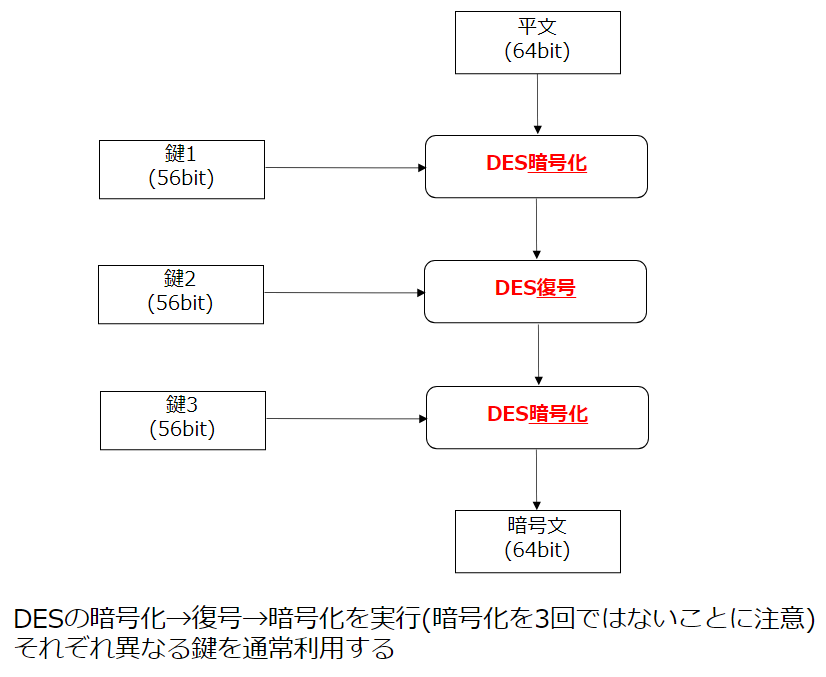
利用シーン

クレジットカードなどのICカードではまだ利用される場合もある²
現状は利用を推奨されていないこともあり、AESへの置き換えが進んでいる

AES

概要³

※概要図に関しては、ブロック長(128bit)、鍵長(128,192,256bit)が異なるだけで他はDESと同じになるため、省略

以下の処理を1ラウンドとして暗号化を行う。
復号の場合はその逆の処理を行う。
鍵長に応じて、10~14回のラウンドを繰り返す。

• SubBytes：換字表（Sボックス）による1バイト単位の置換。
• ShiftRows：4バイト単位の行を一定規則で左シフトする。
• MixColumns：ビット演算による4バイト単位の行列変換。
• AddRoundKey：ラウンド鍵とのXORをとる。

利用シーン

無線LANの暗号方式(WPA2)、SSL/TLS通信の暗号方式など幅広い分野にて利用されている

モード

ブロック暗号(DES、AESなど)の繰り返し方法の種類のこと。
例えば、AES-CBCなどのように、[ブロック暗号]-[モード]で記載されることもある。
この場合は、AES暗号をCBCモードで繰り返し実行する、という意味合いになる。
CRYPTREC暗号リストを参考に、以下でよく利用されるモードの一部について説明をしていく。

ECBモード

• 平文ブロックと暗号文ブロックが1対1の関係になる
• 機密性が低いため利用には注意が必要
  (同じ値の平文ブロックが存在した場合、それらは全て同じ値の暗号文ブロックになってしまい、暗号解読のきっかけとなる可能性があるため)
• そのため利用は推奨されていない

CBCモード

• ECBモードの機密性が低いという欠点はCBCモードにはない
  (1つ前の暗号文ブロックとXORを取り暗号化するため)
• 途中の平文ブロックだけを暗号化することはできない
  (例：暗号文ブロック3を作りたい場合は、暗号文1,2ブロックを計算した後でないといけない)

CTRモード

• カウンタの初期値は暗号化のたびに異なる値(NONCE)を元に生成⁴
• 暗号化と復号が全く同じ構造になる
• 鍵ストリームは事前に準備可能(カウンタと暗号アルゴリズムさえ分かれば準備できるため)

公開鍵暗号

※公開鍵暗号ってどんなもの？という方は前回の記事をご覧ください。

歴史的な背景

• 1976年、最初の公開鍵暗号のアイディアが発表される(暗号鍵/復号鍵の鍵を分ける、といった特性を備えている案)
• 1978年にRSAが発表された。RSAは現在の公開鍵暗号のデファクトスタンダードとなっている
• 近年、RSAの危殆化⁵を見越して、楕円曲線暗号(ECC)の利用も増えてきている⁶
• 楕円曲線暗号(ECC)はRSAよりも短い鍵長で同等の暗号強度⁷を実現する

RSA

概要

• 公開鍵ペア(E,N)と秘密鍵ペア(D,N)により、暗号/復号処理が可能
• 今後利用する場合は、2048bit以上の鍵長が推奨されている
• 平文のハッシュ値を入力として使うことで、RSAの処理時間を削減するケースもある

利用シーン

インターネットのデジタル署名が最も有名な利用シーンと思われる

楕円曲線暗号(ECC)

概要

楕円曲線暗号とは、楕円曲線を使った暗号技術全般のことで、

• 楕円曲線を用いた公開鍵暗号 → 今回説明
• 楕円曲線を用いた鍵交換 → 今回説明
• 楕円曲線を用いたデジタル署名 → 別途説明

などの総称になる。
楕円曲線の種類はP-256など様々あり、それぞれ曲線の形状(パラメータ)が異なる。

楕円曲線を用いた公開鍵暗号

参考サイトの図が概要をとらえやすいため、参考にさせていただく。

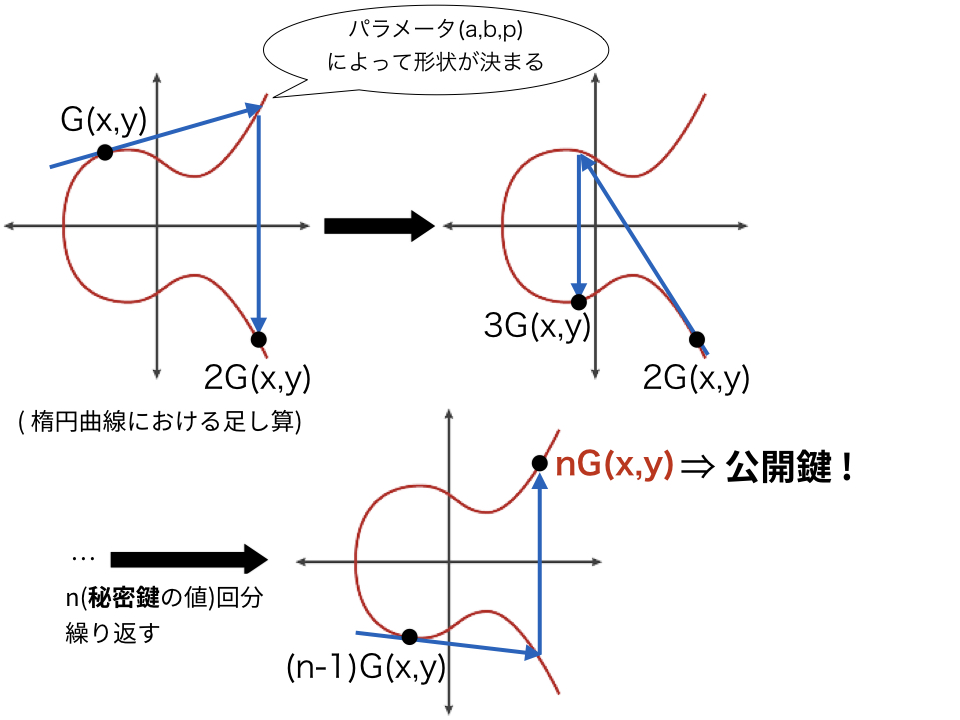
• ベースポイント：G(x,y)
• 秘密鍵：n(スカラー値⁸)
• 公開鍵：nG(x,y)

ベースポイントを出発点として、楕円曲線上の足し算を秘密鍵(スカラー値)の回数分繰り返すことで公開鍵を求めることができる

楕円曲線を用いた鍵交換

• ベースポイントG(x,y)は同じ楕円曲線(例：P-256)を選択することで同じ値を共有できる
• 秘密鍵は乱数のため、通信ごとに異なる乱数を使えば、共通鍵も通信ごとに変えることが可能
  (= 過去の通信の機密性が破られることはなくなる：前方秘匿性)

利用シーン

RSAの代わりとして使われることが多いため、インターネットのデジタル署名が最も有名な利用シーンと思われる

暗号強度

2031年度以降も継続利用したい場合は、128bitの暗号強度の暗号スイート⁹を利用すべき

まとめ

共通鍵暗号、公開鍵暗号の具体的なアルゴリズムを学ぶことができた
次回は具体的な利用例として、デジタル署名 及び 証明書について勉強していきたい

1. https://ja.wikipedia.org/wiki/%E5%85%B1%E9%80%9A%E9%8D%B5%E6%9A%97%E5%8F%B7 ↩

2. https://ja.wikipedia.org/wiki/%E3%83%88%E3%83%AA%E3%83%97%E3%83%ABDES ↩

3. https://ja.wikipedia.org/wiki/Advanced_Encryption_Standard ↩

4. 生成例：ブロック長が16byteの場合、カウンタの初期値は[上位8byte NONCE][下位8byte ブロック番号]とする。カウンタの増加は[下位8byte ブロック番号]をカウントアップしていく ↩

5. アルゴリズムが破られるなど安全性のレベルが低下した状態 ↩

6. https://jp.globalsign.com/support/ssl/about-ecc.html ↩

7. 暗号文がどれだけ解読しにくいかを表した指標。参考 ↩

8. 通常の数値のこと。ベクトル(座標値)を利用するため、そちらと区別するのにスカラーという呼称を使う ↩

9. 暗号アルゴリズムやハッシュ、鍵長などの設定の組み合わせのこと ↩