- 参考書は時系列分析の定番本 沖本先生の経済・ファイナンスデータの計量時系列分析.
定常性について理解する
定常性とは?
- 定常性(stationarity)は時系列モデルの最も基本的な概念.
- 定常性の仮定のもとで基礎的な時系列モデルを構築し、そのモデルを基に非定常なモデルが構築される.
- 定常性とは、同時分布や基本統計量の時間不変性に関するものである.
- 何を不変とするかによって, 弱定常性(weak stationary)と強定常性(strong stationary)に分類される.
弱定常性の定義
定義1.1(弱定常性) 任意のtとkに対して,
$$
E(y_t) = \mu \\
Cov(y_t,y_{t-k}) = E[(y_t - \mu)(y_{t-k} - \mu)] = \gamma_k
$$
が成立する場合, 過程は弱定常(weak stationary)といわれる.
- 定義から, 自己共分散は時点によらず, 時間差kにのみ依存する.
- したがって, 任意のkに対して, γk = γ−k の関係が成り立つ
- 自己共分散だけでなく, 自己相関も時点には依存せず, 時間差kにのみ依存する.
$$
Corr(y_t,y_{t-k}) = \frac{Cov(y_t,y_t-k)}{\sqrt{var(y_t)}\sqrt{var(y_{t-k})}}= \frac{\gamma_k}{\gamma_0} = \rho_k
$$
- 上の式の分母の分散は, 時系列での分散の意味を考えると, kによらず一定であることに注意
- 自己共分散の式において, k=0とおいたときの値が, その時系列の分散を表す
- ρk = ρ−kも成り立つ
日常用語で説明すると
- 定常性とは要するに..
- 平均に回帰し, 長期的にはどちらに動くか予測できる
- 自己相関は指数的に減衰し、ショックは一時的な影響
- トレンドはもたない
- イメージ的に...
- ある値の周りをなんとなく同じような振れ方で振動しているようなデータ
- 任意の区間を取って, フーリエ変換しても同じ結果が得られる, みたいなデータ
- 逆に, ちょっとずつある周波数成分が大きくなっていく, みたいなデータは非定常
素朴な疑問
- 弱定常性は有限時間のなかでどうやって判定するのだろうか?
- 期待値が一定という条件ってどういう意味なんだ?データは一回きりなのに.
- 適当な期間を区切って, 窓をスライドさせて, スライドさせても平均が不変, とするということか?
- 例えば"あ〜〜"とか発声をスペクトルアナライザでみて, それが一定以内の変動なら定常, とか
- どれくらいの長さの窓なら妥当なのだろうか..声とかならある程度物理的な時間があるかな
- 弱定常ってことは, 時系列を構成する個々の波成分の周期が時間変動しない, 安定的ってこと?
- イメージ的にはリアルタイムFFTをして, ずっとスペクトルが変わらない状態って感じ?
- でもそのFFTの時間スパンはどれくらいだと妥当なのか?よくわからん。
定常なデータと非定常なデータの具体例
数式だけではよくわからない。具体例をみてイメージをつかもう。
例示は理解の試金石!
定常過程の例
- ホワイトノイズ
- 歴代内閣支持率(とても定常にみえないが、検定すると定常となる)
- 日経平均株価の1階差分
非定常過程の例
- ランダムウォーク
- 株価
- GDP
弱定常過程の代表例 -ホワイトノイズ-
定義1.4(ホワイトノイズ) すべての時点tにおいて
$$
E(\epsilon_t) = 0\\
\gamma_k = E(\epsilon_t \epsilon_{t-k}) =
\begin{cases}
\sigma^2 & k = 0 \\
0 & k \neq 0
\end{cases}
$$
が成立するとき、ϵtはホワイトノイズ(white noise)と呼ばれる.
- すべての時点において期待値が0である.
- 分散は一定値である.
- 自己相関をもたない.
- 正規過程に従うホワイトノイズは, 正規ホワイトノイズと呼ばれる.
- 正規過程とは?まだよくわからん。。
- パワースペクトルでみると, どの周波数も同じ強度になる
- ホワイトの由来は, 可視領域の広い範囲をまんべんなく含んだ光が白色であることによる
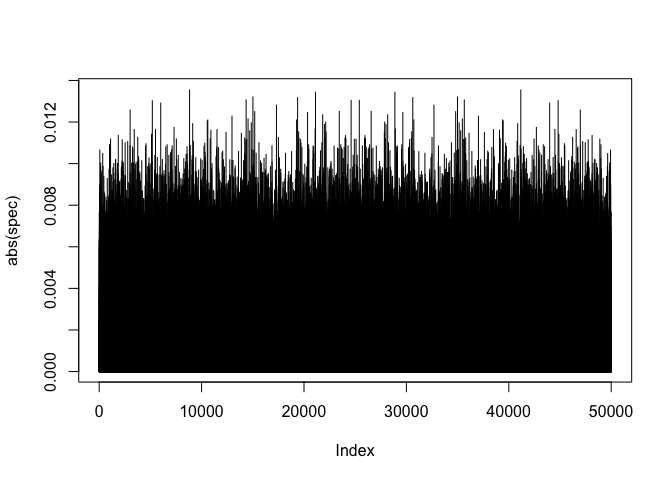
- フーリエ変換してスペクトルを確認してみる
- 確かに, すべてのスペクトルの強度がほぼ一定になっていることがわかる.
弱定常性について補足
- 経済・ファイナンスの分野では, 単に定常性というと, 弱定常性を指すことが多い.
- 条件付き期待値や条件付き分散は時変的でもよいことに注意.
- 実際の生の時系列データの殆どは定常性がないが, 差分をとったり, トレンドや季節性を取り除くことで, 定常過程に変換することが多い.