ケプストラム解析の自分用まとめ

はじめに

このページは自分用に下記ページを書き直した物です
もしケプストラムの解説を求めて当ページに来た方がいましたら下記のページを御覧ください
ケプストラム分析 - 人工知能に関する断創録
メル周波数ケプストラム（MFCC） - Miyazawa’s Pukiwiki

ケプストラム解析

ケプストラム（英: Cepstrum）とは、音のスペクトルを信号と見なしてフーリエ変換 (FT) した結果である。"spectrum" の最初の4文字をひっくり返した造語。ケプストラムには、複素数版と実数版がある。

ケプストラムは、異なるスペクトル帯における変化の度合いに関する情報と見ることができる。本来、地震や爆弾の爆発を原因とする地震性反響の特性を調べるために考案された。また、レーダー信号の反射を解析するのにも使われてきた。(wikipediaより)

ケプストラム解析の用途として、スペクトルの周期情報の抽出、スペクトルの包絡線（エンベロープ）をもとめる、ことなど

概要

口語的定義: （信号の）ケプストラムとは、（信号の）フーリエ変換の対数（位相アンラッピングを施したもの）をフーリエ変換したものである。スペクトルのスペクトルとも呼ばれる。

数学的定義: 信号のケプストラムは FT(log(|FT(信号)|)+j2πm) である。ここで m は、複素対数関数の虚数成分または角度の位相アンラッピングを正しく行うのに必要とされる整数である。

アルゴリズム的定義: 信号 → FT → abs() → log → 位相アンラッピング → FT → ケプストラム

計算

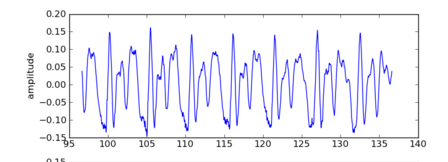
元データ

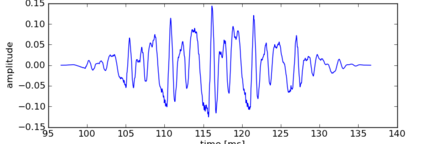
窓関数をかける

$w(x)=0.5-0.5cos2πx, if0≦x≦1$(ハン窓の場合)

import numpy as np
# ハニング窓をかける(窓関数はハミング窓等も可能)
hanningWindow = np.hanning(len(wavdata))
wavdata = wavdata * hanningWindow

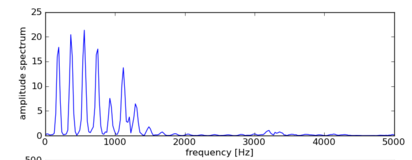
フーリエ変換する(振幅は合わせてない)

n = 2048  # FFTのサンプル数 2のn乗
# 離散フーリエ変換
dft = np.fft.fft(wavdata, n)
# 振幅スペクトル
Adft = np.abs(dft)
# パワースペクトル
Pdft = np.abs(dft) ** 2
# 周波数スケール
fscale = np.fft.fftfreq(n, d = 1.0 / fs)

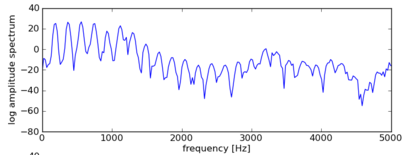
対数スペクトルにする $Y(x)=log_{10}(x)$
(この時$Y(x)=20log_{10}(x)$にするとdBの単位になる？)

# 対数振幅スペクトル
AdftLog = 20 * np.log10(Adft)
# 対数パワースペクトル
PdftLog = 10 * np.log10(Pdft)

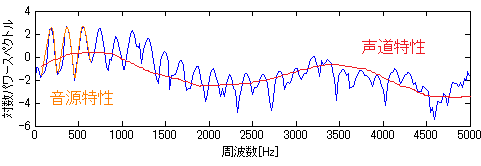
なだらかに変動するスペクトル包絡（赤線）と細かく変動するスペクトル微細構造（青線）があることがわかる

すなわち、フーリエ変換の結果も周期性のある信号であるといえる

フーリエ変換後のスペクトルは色々な振動がかけ合わさった物(畳み込まれた物)といえるが、対数をとってやることで単純に足し合わせた物として考える事ができる

→分離ができる

• スペクトル領域では$Y(w)=S(w)H(x)$
• 対数スペクトル領域では$Y(w)=S(w)+H(x)$

ケプストラム（cepstrum）

対数スペクトルをもう一度フーリエ変換にかけて、音源の周波数と声道の周波数を切り分けることを考えます

• フーリエ変換のフーリエ変換は、フーリエ変換の結果に対して逆フーリエ変換をかけるのと同じ処理になる
• 対値をとっているので、（実数ケプストラムでは）位相スペクトルの情報は消える

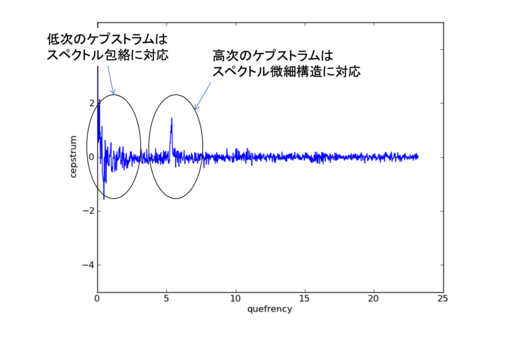
y軸：ケプストラム
スペクトル領域を逆フーリエ変換するので元の時間領域に戻るが、対数をとっているので元の信号にはならずにケプストラム（cepstrum）と呼ばれるものになる

x軸：ケフレンシー
周波数の逆数のようなものなのでケフレンシー（quefrency）一応尺度的には時間の尺度

# ケプストラム分析
# 対数スペクトルを逆フーリエ変換して細かく振動する音源の周波数と
# ゆるやかに振動する声道の周波数を切り分ける
cps = np.real(np.fft.ifft(AdftLog))
quefrency = time

参考

ケプストラム分析 - 人工知能に関する断創録
メル周波数ケプストラム（MFCC） - Miyazawa’s Pukiwiki
https://ja.wikipedia.org/wiki/ケプストラム