はじめに
MLTK 5.0 (もしくは 4.4) に新しく登場した System Identification というアルゴリズム。
一番の特徴は影響が起こるのに時間がかかるようなケースにおいて、各属性値の過去のデータも加味した予測ができるようになるとのことです。
例えば飲み過ぎた次の日に頭が痛くなる（私は大体そう）かどうかを予測する場合、単純にある時点の飲んだ量や種類のデータだけから予測するよりも、それまでの時間ごとの飲んだ量や種類のデータなど過去の動的データを使い予測ができるというものです。
Splunkのように時系列データがメインの場合は非常に役に立つアルゴリズムだと思われます。
ということで、まずは試してみたいと思います。
System Identificationとは？
システム同定（システムどうてい、System Identification）とは、計測データから動的モデルを構築するための数学的ツールやアルゴリズムを指す用語。動的モデルとはシステムやプロセス（過程）の動的振る舞いに関する数学的記述を意味する。
by wikipedia
これって基本的に機械学習の考え方ぽく見えるのですが、元々は制御工学で使われていた用語らしく、ブラックボックスな物に対してインプットとアウトプットから中身の動きを予測する方法として用いられていたぽいです。
また動的モデルという箇所がポイントで前のデータと今回のデータ間で何かしらの関係があるようなデータが対象となります。わかりやすい例として時系列データがあります。状態空間モデルともいうらしいです。
ざっくりとした用語理解はこれくらいにして、Splunkで今回実装された System Identification アルゴリズムの特徴を整理してみますと。
- 線形・非線形データモデルを作成できる
- Multi-layer Neural Network を利用する
- incremental fit が可能。
- numeric field のみサポート
parameter 理解
複数のパラメータが用意されているので、簡単にチェックしたいと思います。マニュアル参照
-
dynamics : 必須
- どこまで過去のデータを利用するか指定する
- 属性値（目的変数＋説明変数）の数だけ指定が必要。
- 各属性値のラグをそれぞれ記載する
- 例） 目的変数 targetA, 説明変数 B,C,D があったとする。それぞれ lagを考慮するデータポイントを 1,2,3,4 とすると、dynamics=1-2-3-4
-
conf_interval : default=95
- 信頼区間を指定する。 (upper / lower)
-
layers : default = 64-64
- 隠れ層と、各層の NN の数
- 例） 64-32-64 64個 - 32個 - 64個の３層の NN
-
epochs : default = 500
- 学習する回数
試してみよう
それでは早速試してみたいと思います。
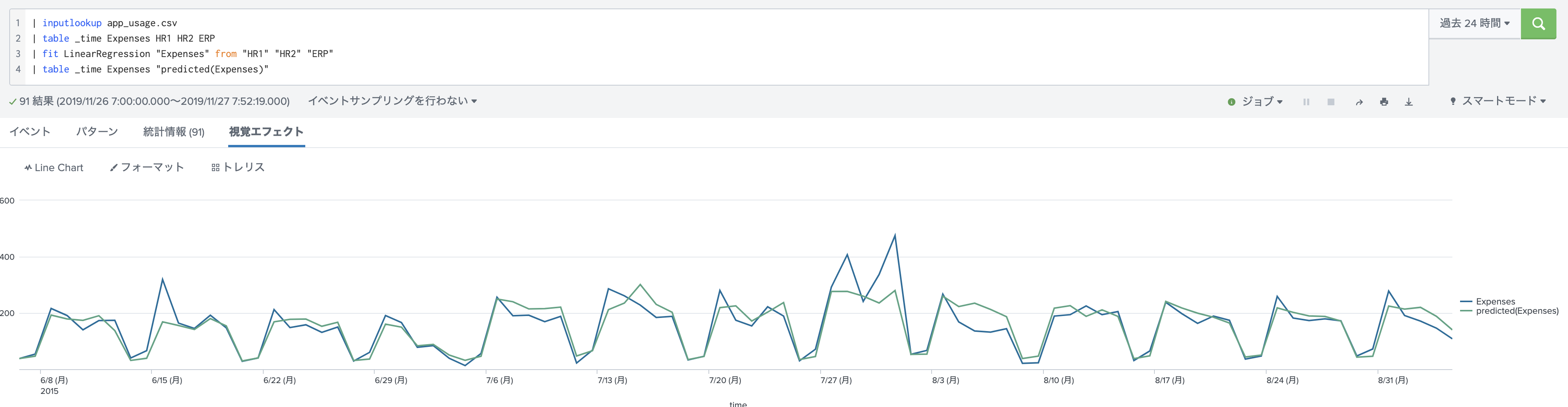
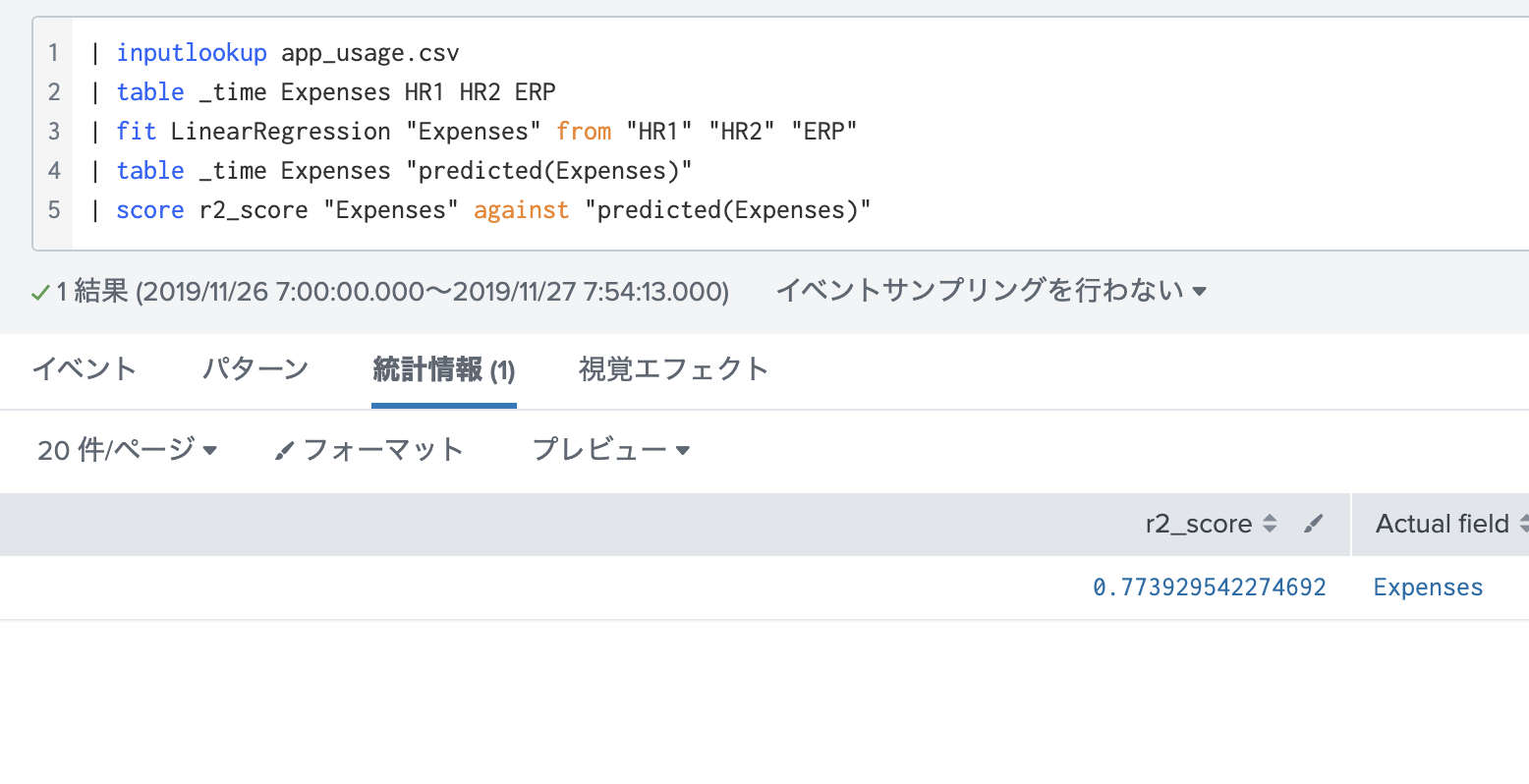
検証１: LinearRegressionを使った結果
まずは従来のアルゴリズムを使って予測モデルを作ってみます。今回は LinearRegression を使ってみます。
| inputlookup app_usage.csv
| table _time Expenses HR1 HR2 ERP
| fit LinearRegression "Expenses" from "HR1" "HR2" "ERP"
| table _time Expenses "predicted(Expenses)"
スコアを出してみると 77.4% の正解率でした。
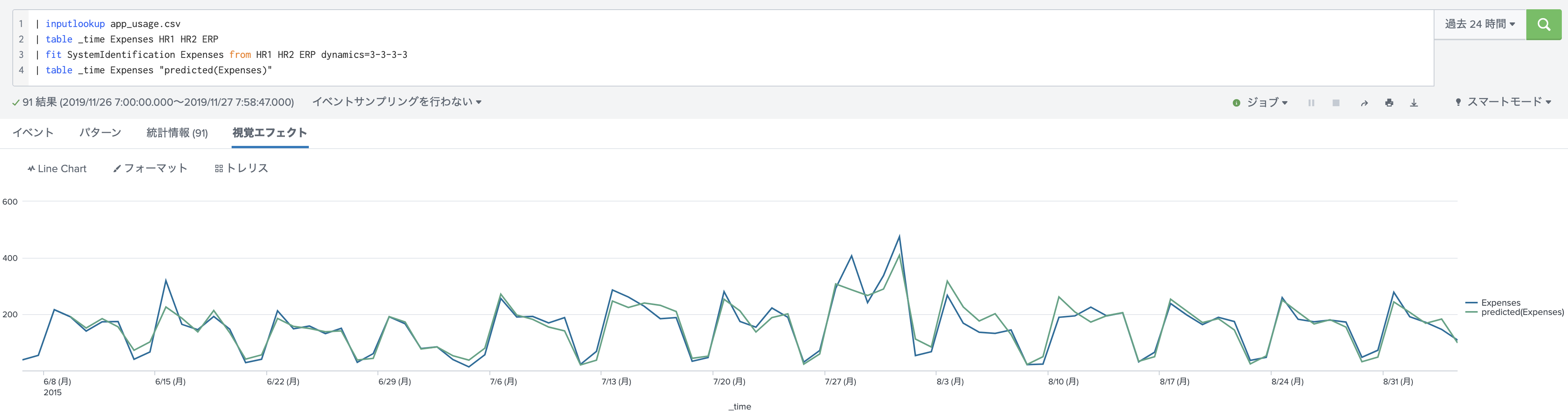
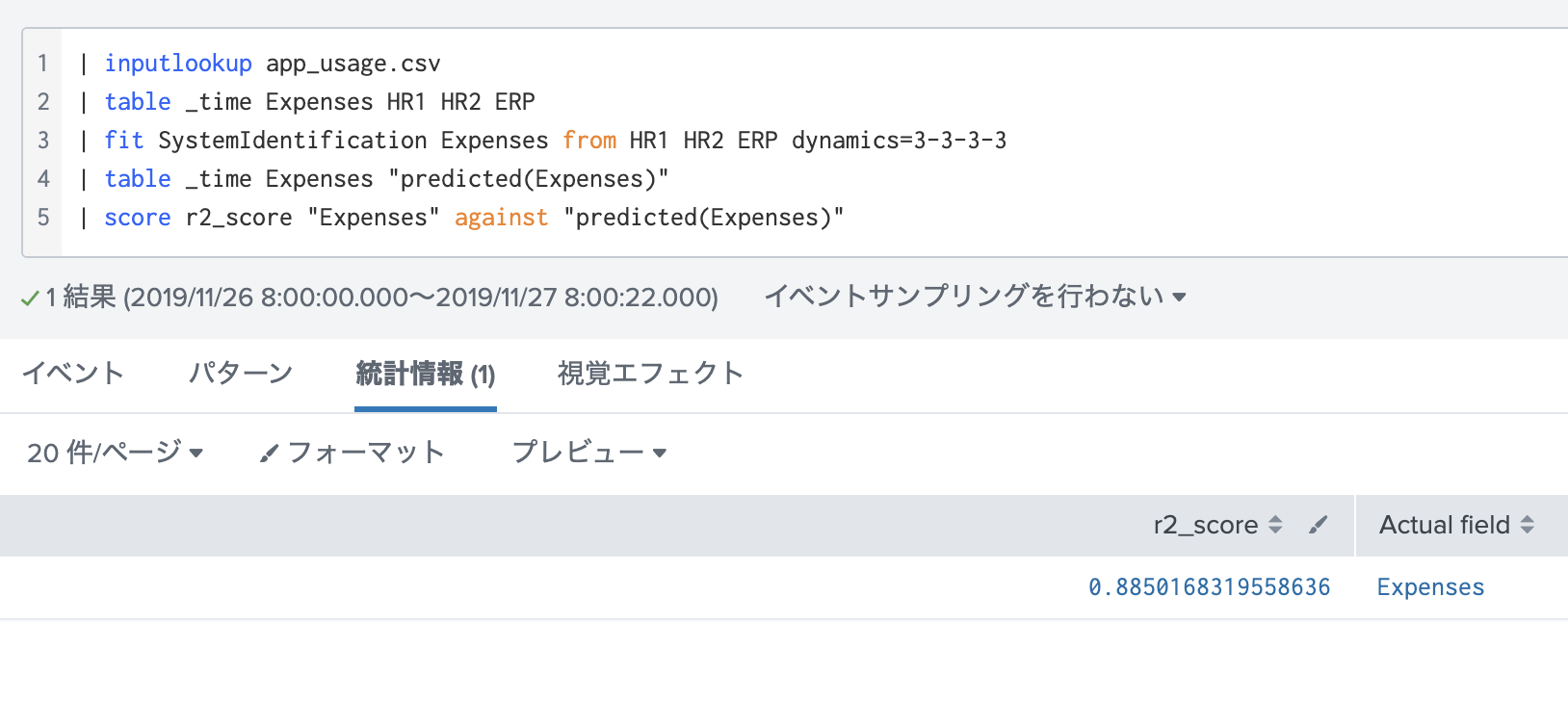
検証２： System Identification を使った結果 (過去データ３つを利用）
| inputlookup app_usage.csv
| table _time Expenses HR1 HR2 ERP
| fit SystemIdentification Expenses from HR1 HR2 ERP dynamics=3-3-3-3
| table _time Expenses "predicted(Expenses)"
スコアを出してみると、なんと88.5%!!
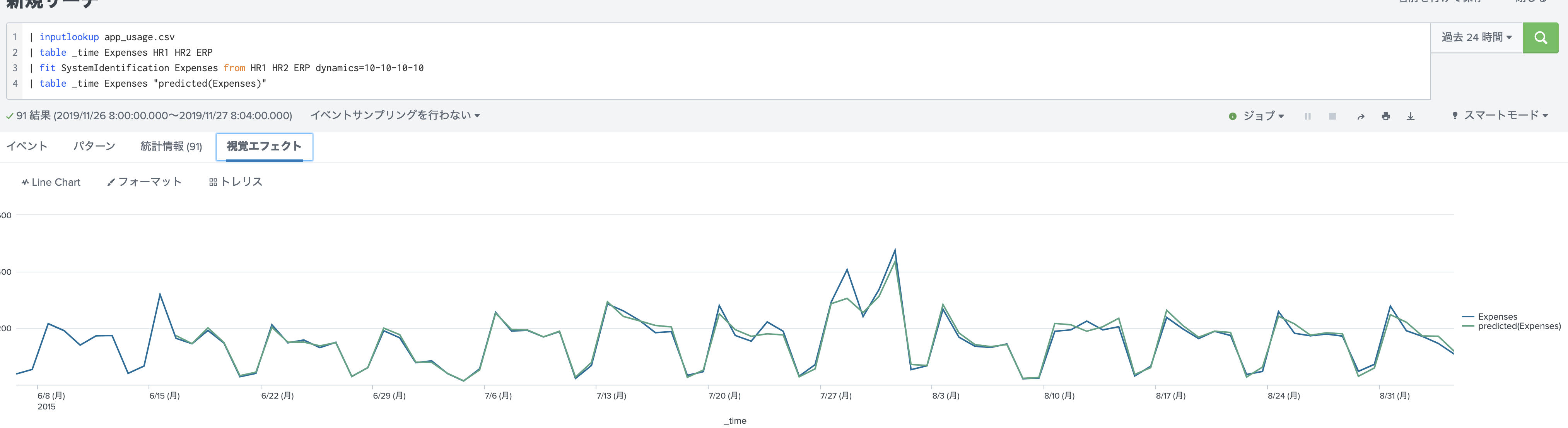
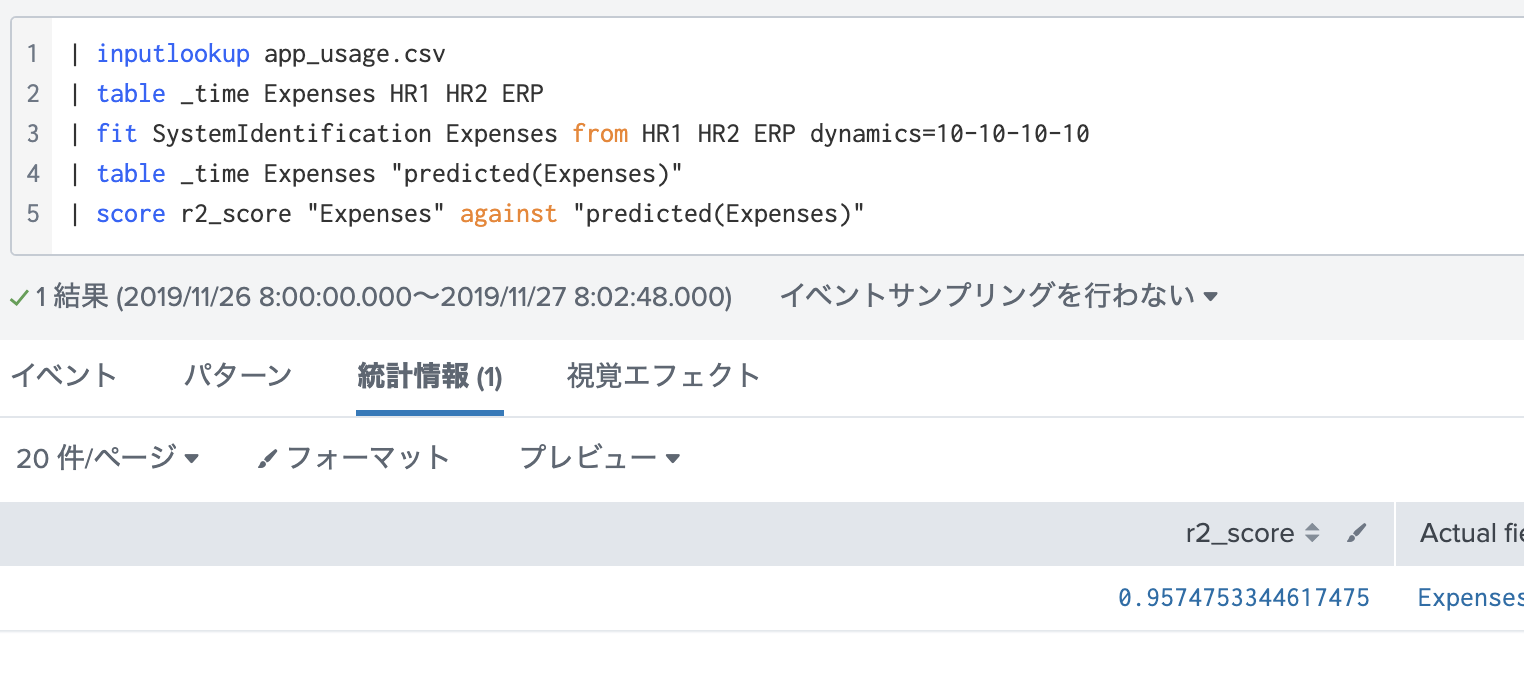
検証３： System Identification を使った結果 (過去データ１０個に増加）
過去データを増やせば結果もよくなるのでは？と思い、データポイントを１０個に増やしみました。
| inputlookup app_usage.csv
| table _time Expenses HR1 HR2 ERP
| fit SystemIdentification Expenses from HR1 HR2 ERP dynamics=10-10-10-10
| table _time Expenses "predicted(Expenses)"
スコアを出してみると、驚異の95.7%!!
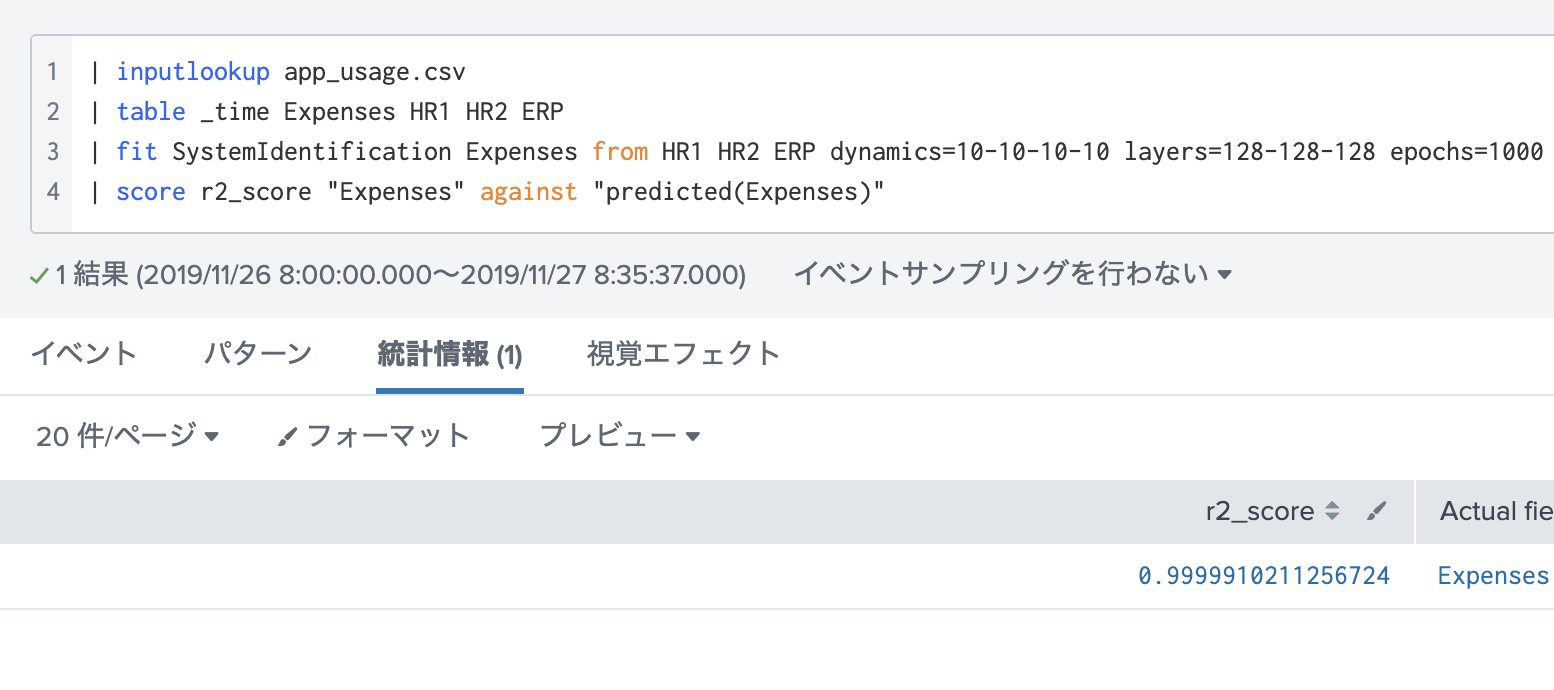
検証４： System Identification を使った結果( Neural Network を 128 x 128 x 128 の 3layerにして、epochs=1000にする）
| inputlookup app_usage.csv
| table _time Expenses HR1 HR2 ERP
| fit SystemIdentification Expenses from HR1 HR2 ERP dynamics=10-10-10-10 layers=128-128-128 epochs=1000
| score r2_score "Expenses" against "predicted(Expenses)"
スコアはな・な・なんと99.9%
結果
それぞれのスコアは以下の通りです。
| LinearRegression | System Identification(データラグ３つ） | System Identification(データラグ10個） | System Identification(NN:128-128-128,epochs=1000) |
|---|---|---|---|
| 77.4% | 88.5% | 95.7% | 99.9% |
今回は訓練データのみのため過学習の可能性を考慮しないといけないのですが、従来のアルゴリズムに比べて特徴データが増える分精度は高くなるのは納得です。気になる点としては NNを使っているので学習コストが高い点です。今回のデモデータだと９０個ほどしかなかったので問題になりませんでしたが、大きくなると学習時間に影響が出ると思われます。この点は要注意して使った方が良さそうです。
とはいえ時系列データで特定フィールドの予測をする場合、従来よりも高い精度の結果が期待できるアルゴリズムだなと感じました。