こんにちは、bitFlyerのAdvent Calendar 14日目 の記事です。
最近めっきり寒くなってきましたね。
そして、卒論の季節ですね。友人や後輩たちが慌て始めていて思い出しました。
ちなみに私の学生時代はというと・・・この時期はまだ焦っていませんでした。
焦っておけば良かったです。
友人たちの助けを借りてなんとか卒業できましたが、未だに卒業できない夢を頻繁に見ます。
大学生は人生の夏休みとよく言われていますが、辛かった卒論の記憶と辛かった実験の記憶しかありません。
実験結果を、考察のためにFortran(古い言語)で積分して誤差を出してレポートに「誤差が小さかった」と書いたら「小さいって何を基準に?定量的に書いてください」と教授に激詰めされた記憶や、毎週燃えるゼミ発表などなど枚挙に暇がありません。
ところで、皆さんはプログラミングで積分をしたことはありますでしょうか?
x^2を積分したらx^3/3になりますが、それをプログラムでどう書けば良いでしょうか。
このくらいの積分なら結果を使ってしまえば良いのですが、解析的に解けない場合もあります。
ニッチすぎるとは思いつつ、懐かしかったので今回はプログラミングにおける積分について書いてみます。
長方形を用いてx^2を定積分してみる
積分区間は[0, 1]とします。
理論値は
[x^3/3] = 1/3
ですね。
実際にこれに近い値を計算していきます。
真っ先に考えつく方法としては、長方形で近似する方法かと思います。
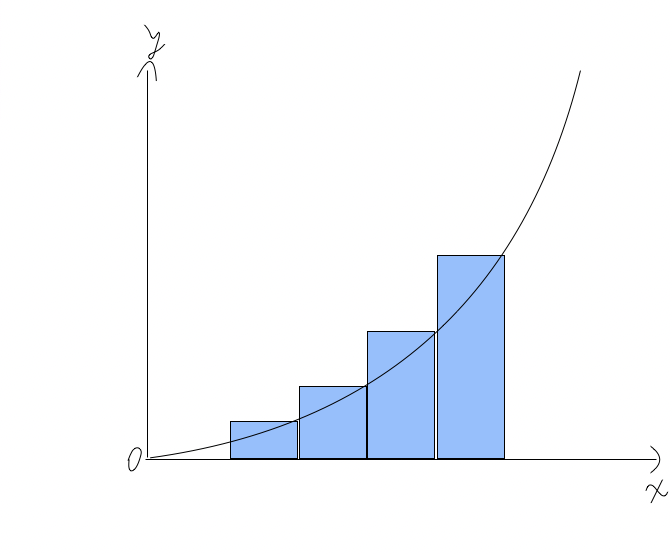
上記の図のように、積分区間に長方形を並べて面積を足し上げることで面積の近似ができます。
この要領で早速計算してみます。
fun main(args: Array<String>) {
for (i in 1..30) {
val rectSum = integralByRect(i)
println(rectSum)
}
}
/**
* nは積分区間の分割数
*/
fun integralByRect(n: Int): Double {
var sumV = 0.0
val dx = 1.0 / n
for (i in 1..n) {
val x = i * 1.0 / n
val y = f(x)
val ds = dx * y
sumV += ds
}
return sumV
}
fun f(x: Double): Double {
return x * x
}
やっていることは図に書いたものと同じで、積分区間をnで分割して長方形の面積を足し上げる関数を定義しています。
分割数を1から30まで動かして出力してみました。
1
0.625
0.5185185185
0.46875
0.44
0.4212962963
0.4081632653
0.3984375
0.3909465021
0.385
0.3801652893
0.3761574074
0.3727810651
0.3698979592
0.3674074074
0.365234375
0.3633217993
0.3616255144
0.3601108033
0.35875
0.3575207861
0.3564049587
0.3553875236
0.3544560185
0.3536
0.3528106509
0.3520804755
0.3514030612
0.3507728894
0.3501851852
分割数を30にしたときの値は 0.3501851852 でした。
理論値 0.33333...と比較してみて、思ったより良い精度ですね(全く定量的ではなくただの感想なので、どうか教授が見ていないことを祈ります)
ちなみに1000分割すると0.3338335000000003 となりました。ますます良い精度ですね。
頑張って沢山分割すればある程度良い精度が出ることがわかりました。
しかし、「曲線を長方形で近似するってどうなの???」と学生の私は疑問に思いました。
そのすぐ後に、台形で近似する方法を知ってとても感動したのを覚えています。
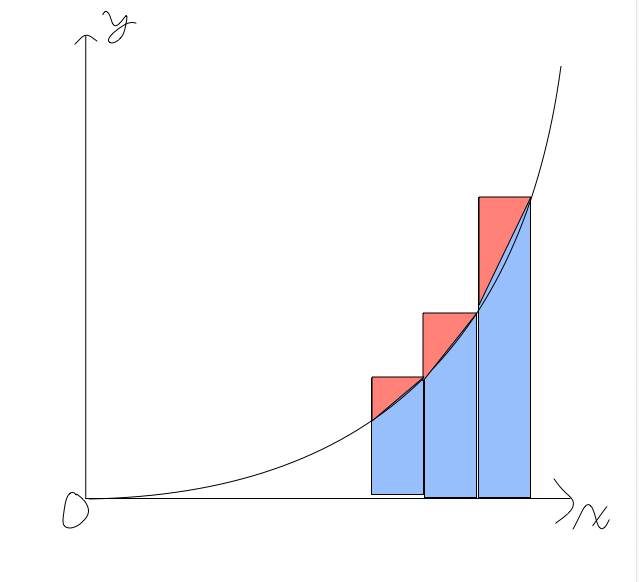
台形を用いてx^2を定積分してみる
図で表すと下記のようになります。赤くなった三角の部分の面積を足すのは明らかに余計なので、この面積を引いてみます。
fun main(args: Array<String>) {
for (i in 1..30) {
val trapezoidSum = integrateByTrapezoid(i)
println(trapezoidSum)
}
}
/**
* nは積分区間の分割数
*/
fun integrateByTrapezoid(n: Int): Double {
var sumV = 0.0
val dx = 1.0 / n
for (i in 1..n) {
val x = i * 1.0 / n
val y = f(x)
val dy = f(x) - f(x - dx)
val ds = dx * y - 0.5 * dx * dy
sumV += ds
}
return sumV
}
fun f(x: Double): Double {
return x * x
}
先ほどの長方形の足し上げの際に、三角形の余分な部分の面積を差し引いています。
これで精度が上がること間違いなしです。
出力結果は
0.5
0.375
0.3518518519
0.34375
0.34
0.337962963
0.3367346939
0.3359375
0.3353909465
0.335
0.3347107438
0.3344907407
0.3343195266
0.3341836735
0.3340740741
0.333984375
0.3339100346
0.3338477366
0.3337950139
0.33375
0.3337112623
0.333677686
0.3336483932
0.3336226852
0.3336
0.3335798817
0.333561957
0.3335459184
0.3335315101
0.3335185185
なんとたった30分割で 0.3335185185 まで近似できました。
ほぼ 1/3 ですね。
長方形を用いた 0.3501851852 という結果より遥かに誤差が小さいです。
ちなみに1000分割すると 0.33333349999999984 になりました。もはや1/3と言っても過言ではないです。
定積分を長方形/台形で近似したときの誤差率

台形の場合はあっという間に誤差率がほぼ0に収束していきますね。
ちなみに参考までに、xの対数をとったら誤差率は下記のようになりました。(線形になったような記憶があるのですが、記憶違いかもしれません)

終わりに
ニッチすぎる記事でしたが、もしKotlinで積分したい人がいたら参考にしてください!
また、卒論を控えている方がもし見ていたら頑張ってください、応援しています。
最後に、弊社bitFlyerではAndroidエンジニアを募集しています。ご興味のある方はぜひご応募ください!