先のアメリカ合衆国大統領選挙において、こんな記事がありました。
ベンフォードの法則（ベンフォードのほうそく、Benford's law）とは、自然界に出てくる多くの（全てのではない）数値の最初の桁の分布が、一様ではなく、ある特定の分布になっている、という法則である。(Wikipediaより)
なるほど、これは面白い！ 自分も試してみたくなったので、Pythonにてフルスクラッチ実装してみました。
まずは、日本の市区町村の人口分布、面積、人口密度がベンフォードの法則に合致するかを調べてみます。
↓データは下記のサイトを使わせていただきました。
https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00200521&tstat=000001049104
データテキスト「data.txt」はこんな感じでタブ区切り
横浜市 3,724,844
大阪市 2,691,185
名古屋市 2,295,638
札幌市 1,952,356
福岡市 1,538,681
・・・
(略)
Pythonで書いたコードはこれ。
data_list = open('data.txt', encoding="utf-8")
head = [0,0,0,0,0,0,0,0,0,0]
pct = [0,0,0,0,0,0,0,0,0,0]
benford = [0, 30.1, 17.6, 12.5, 9.7, 7.9, 6.7, 5.8, 5.1, 4.6]
total = 0
for name_num in data_list:
name,num = name_num.split("\t")
num = int(num[0])
for xx in range(0, 10):
if num == 0:
head[0] += 1
break
elif xx == num:
head[xx] += 1
total += 1
break
with open("dataafter.txt", "a", encoding="utf8", errors="replace") as file:
for xx in range(1, 10):
pct[xx]=head[xx]/total * 100
file.write('{0}\t{1}\t{2:.1f}%\t{3}%\t{4:.1f}%\n'.format(xx,head[xx],pct[xx],benford[xx],pct[xx]-benford[xx]))
file.write('備考:0\t{0}\t--\n'.format(head[0]))
file.close()
1916件の有効データ(data.txt)から得られた結果↓(dataafter.txt)。
1 590 30.9% 30.1% 0.8%
2 300 15.7% 17.6% -1.9%
3 254 13.3% 12.5% 0.8%
4 182 9.5% 9.7% -0.2%
5 159 8.3% 7.9% 0.4%
6 110 5.8% 6.7% -0.9%
7 125 6.5% 5.8% 0.7%
8 105 5.5% 5.1% 0.4%
9 87 4.6% 4.6% -0.0%
備考:0 4 --
おお！全て2％未満の誤差に収まりました！
※表の見方
左から・・・
先頭に出現した数字、出現した回数、出現した割合、ベンフォードの法則、法則との差。(人口が0の自治体4つは計算外)
グラフにして見やすくするために、下記のコードを追加してみました。
import numpy as np
import matplotlib.pyplot as plt
left = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
height = np.array([pct
[1], pct[2], pct[3], pct[4], pct[5], pct[6], pct[7], pct[8], pct[9]])
height2 = np.array([30.1, 17.6, 12.5, 9.7, 7.9, 6.7, 5.8, 5.1, 4.6])
plt.bar(left, height,tick_label=left,width=0.4)
plt.plot(left,height2,linestyle='solid',color='k',marker='^',label='B')
plt.title("ベンフォードの法則検証", fontname="meiryo")
plt.ylabel('パーセント',fontname="meiryo")
plt.savefig("img.png")
そのグラフがこれ
【人口】
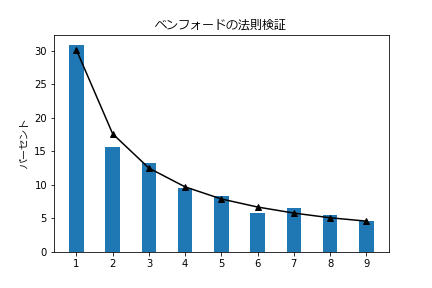
棒グラフが人口の最初のケタの数字の分布。
折れ線グラフがベンフォードの法則。
なるほど、だいたい一致してますね。
dataafter.txtを見やすいようにテーブル型に手動修正
|先頭数字|出現数|出現率|法則|法則との差|コメント|
|---|---|---|---|---|---|---|
|1|590|30.9%|30.1%|0.8%||
|2|300|15.7%|17.6%|-1.9%|←最大誤差|
|3|254|13.3%|12.5%|0.8%||
|4|182|9.5%|9.7%|-0.2%||
|5|159|8.3%|7.9%|0.4%||
|6|110|5.8%|6.7%|-0.9%||
|7|125|6.5%|5.8%|0.7%||
|8|105|5.5%|5.1%|0.4%||
|9|87|4.6%|4.6%|-0.0%||
【面積】
面積も2％未満の誤差にすべておさまりました！
|先頭数字|出現数|出現率|法則|法則との差|コメント|
|---|---|---|---|---|---|---|
|1|560|29.2%|30.1%|-0.9%||
|2|359|18.7%|17.6%|1.1%|←最大誤差|
|3|238|12.4%|12.5%|-0.1%||
|4|179|9.3%|9.7%|-0.4%||
|5|143|7.5%|7.9%|-0.4%||
|6|138|7.2%|6.7%|0.5%||
|7|123|6.4%|5.8%|0.6%||
|8|97|5.1%|5.1%|-0.0%||
|9|79|4.1%|4.6%|-0.5%||
【人口密度】
人口密度も全て2%未満の誤差！
|先頭数字|出現数|出現率|法則|法則との差|コメント|
|---|---|---|---|---|---|---|
|1|581|30.4%|30.1%|0.3%||
|2|332|17.4%|17.6%|-0.2%||
|3|217|11.4%|12.5%|-1.1%|←最大誤差|
|4|175|9.2%|9.7%|-0.5%||
|5|168|8.8%|7.9%|0.9%||
|6|116|6.1%|6.7%|-0.6%||
|7|117|6.1%|5.8%|0.3%||
|8|110|5.8%|5.1%|0.7%||
|9|94|4.9%|4.6%|0.3%||
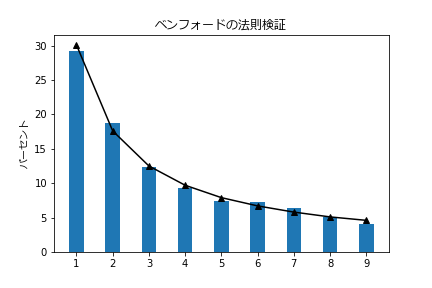
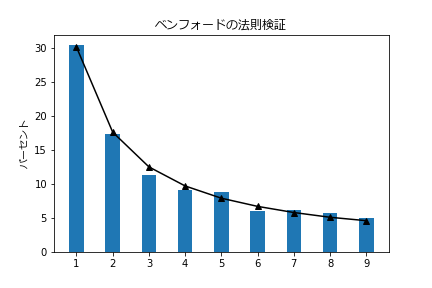
なんと、人口、面積、人口密度が、全てベンフォードの法則通りの分布になってしまいました！
それにしても面積は意外。市町村の面積はそれほどバラツキがないと思ってましたが、実際はかなりの差があるのですね。
日本で一番広い岐阜県の高山市は、香川県や大阪府よりも広いし！
それでは、もっと身近なところで、自分の購入履歴で調査してみましょう。
2009年以降に楽天やamazonなどで買ったものや、エクスペディアなどの旅費の履歴をコピペして計算・・・・。
・・・結構大変だなこの調査・・・・
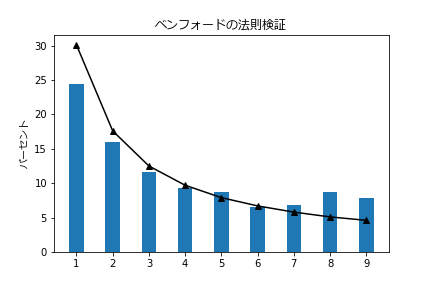
で、出た結果が・・・
・・・・ん？
何か変だぞ？！
なんじゃこりゃ・・・
自分のような変人は、ベンフォード分析でも変な結果になるのかっっ？！・・・
|先頭数字|出現数|出現率|法則|法則との差|コメント|
|---|---|---|---|---|---|---|
|1|124|24.5%|30.1%|-5.6%|←少なすぎ！|
|2|81|16.0%|17.6%|-1.6%||
|3|59|11.6%|12.5%|-0.9%||
|4|47|9.3%|9.7%|-0.4%||
|5|44|8.7%|7.9%|0.8%||
|6|33|6.5%|6.7%|-0.2%||
|7|35|6.9%|5.8%|1.1%||
|8|44|8.7%|5.1%|3.6%|←なんか多い|
|9|40|7.9%|4.6%|3.3%|←なんか多い|
・・・で、よく考えてみたら
買い物をする時に、桁が繰り上がるのを嫌って8000円とか900円あたりの値段で抑えてた気が。。。。
自分の意地汚さがデータに現れてしまいましたorz
しかし、人為的な思惑が混入すると、ベンフォード分析結果が不自然になることが証明されました！
「ベンフォードの法則」すげー！
他にも、ベンフォードの法則は、株価、川の長さ、鉄道、など、あらゆる数値の集合に適用できるそうです。
※身長や偏差値やIQの数値など1桁か2桁の範囲でしか分布しないようなものは使えなかったりします。
一方で、ベンフォードの法則に対しては、懐疑的な意見もありますので、取り扱いは要注意です。
ただし、この法則を仕事で活かせるかは謎です。