Googleデータアナリティクス：サンプル サイズ

はじめに

本記事は、Googleデータアナリティクスのプロフェッショナル認定証のプログラムより、参照させて頂いています。興味を持った方は、是非受講してみてください。

サンプル サイズの重要性

母集団とは あるデータセットに含まれうる すべてのデータ値のことです。 母集団の 100% を 分析に使用できるのであれば それは素晴らしいことです。 しかし、母集団全体に関する 情報収集が不可能な場合もあります。 時間がかかりすぎる、あるいは コストがかかりすぎるためです。

例えば、あるグローバル企業が 猫の飼い主について もっと知りたいとします。 あなたは、カナダに住んでいる 猫の飼い主が好むおもちゃを 調べることになりました。

しかし、カナダには何百万人もの 猫の飼い主がいるので、 彼ら全員からデータを集めるのは 至難の業です。

でも大丈夫、ここでご紹介したいのが サンプル サイズです。 サンプル サイズ、つまり サンプルを使用する場合 母集団を表すような母集団の一部を 使用することになります。 目標は、母集団の中の小さなグループから 母集団全体について 予測や結論を出すのに十分な 情報を得ることです。 サンプルの大きさは 結論が母集団を正確に表している、と 確信できる程度を確認するうえで 役立ちます。 猫の飼い主に関するデータの場合 サンプルサイズは何百万人ではなく 何百人、何千人に関するデータに なるでしょう。

サンプルを使って分析することは 費用対効果が高く、 時間もかかりません。 慎重に熟慮して行えば 猫の所有者全員を探し出して お気に入りの猫のおもちゃを 調べる代わりに サンプル サイズを使用して 同じ結果を得ることができるのです。 しかしもちろん、 潜在的なマイナス面もあります。

サンプリング バイアス

母集団の中の小さなサンプルしか 使用しない場合、 不確実性が生じます。 統計が母集団を完全かつ正確に 表しているかどうか、 100% の確証は得られないのです。 このことは サンプリング バイアスにつながります。 サンプリング バイアスとは サンプルが母集団全体を 代表していないことであり その結果、母集団の特定の要素が 過度に反映されたり、 されなかったりすることをいいます。

例えば、猫の飼い主に関するデータを 収集するための調査で スマートフォンを持っている人だけを 対象とした場合、 スマートフォンを持っていない 猫の飼い主はデータに 含まれないことになります。

ランダム サンプリング

そこで、ランダム サンプリングを使うと サンプリング バイアスに潜む問題を 解決できます。 ランダム サンプリングとは 母集団から無作為に サンプルを抽出する方法であり、 サンプルにあらゆる人々が 等しい割合で選択されるように することです。 猫の飼い主の話に戻りますが ランダムなサンプルを 使用するということは、 あらゆるタイプの猫の飼い主が 等しく選ばれることを意味します。 オンタリオ州のアパートに 住んでいる猫の飼い主も アルバータ州の一軒家に住んでいる 猫の飼い主と同じように 選ばれる可能性があるのです。

データアナリストは、 サンプル サイズの作成は通常、 データに着手する前に行います。 しかし、分析しようとしているデータが 母集団を反映しているか、 目的に沿っているかを 知っておく必要はあります。

サンプル サイズを決める際の注意点

• 30 未満のサンプル サイズは使用しないようにしましょう。サンプルの平均結果が母集団の平均結果を表す最小のサンプルサイズは 30 である、と統計的に証明されています。
• 信頼度は 95％ が最も一般的ですが、場合によっては 90％ でもよいとされています。

以下のような場合には、プロジェクトの必要に応じてサンプルサイズを大きくしましょう。

• 信頼度を上げたい場合
• 誤差を小さくしたい場合
• 統計的有意性を高めたい場合

なぜ、最低 30 以上のサンプル サイズが必要なのか？

この推奨事項は、確率・統計の分野における中心極限定理（CLT）に基づくものです。サンプル サイズが大きくなるにつれて、結果はより多くのサンプルから得られる正規分布（ベル型）に近くなります。30 のサンプルは、CLT が有効とする最小のサンプル サイズです。回帰分析（制御変数と従属変数の間の関係を決定する統計的手法）に基づく研究でも、最小サンプル数は 30 を推奨しています。

サンプル サイズは、解決しようとしているビジネス上の課題の種類によって異なります。

例えば、母集団が 20 万人の都市に住んでいて、18 万人からアンケートに回答してもらうことがもしできれば、それは大きなサンプル サイズと言えます。しかし実際にそのようなことをしなくても、許容できる最小のサンプル サイズはどれくらいなのでしょうか。

調査対象者が市内の全区画を網羅しているのであれば、200 人で良いでしょうか？

回答：解決したい課題によります。

• ビジネス上の課題が、新しい図書館について住民がどのように感じているかを調べることである場合、サンプルサイズは 200 で十分かもしれません。
• ビジネス上の課題が、住民が図書館に資金提供するかどうかにどう投票するかを調べることである場合、200 のサンプル サイズは十分ではないかもしれません。

新しい図書館について住民がどのように感じているかの調査は、図書館の資金調達についてどう投票するかを調査するのと比べて、おそらくより大きな誤差が許容されます。よって投票に関する調査にはより大きなサンプルサイズを使用することになるでしょう。

サンプル サイズが大きいとコストが高くなる

サンプル サイズを大きくすると、より正確な結果が得られる分コストがかかるため、メリットとコストを比較検討する必要があります。新しい製品ラインナップに対する消費者の好みを調査する人は、新薬の効果について調査する人ほど大きなサンプル サイズは必要ないでしょう。医薬品の安全性については、サンプルサイズを大きくすることで得られるメリットの方がコストよりも大きいのです。しかし消費者の好みの場合は、サンプル サイズを小さくしてコストを抑えても、十分な結果が得られるでしょう。

大切なのは基礎を知ること

基礎を知ることで、サンプル サイズに関して正しい選択ができるようになります。小さすぎるサンプル サイズに出くわした場合は、懸念を伝えましょう。サンプルサイズ計算機はそのような時に活用できる素晴らしいツールです。与えられた母集団のサイズに対して、求める信頼度と誤差を入力すれば、統計的にこれらの結果を得るために必要なサンプル サイズを算出してくれます。

表計算ツールを使って最適なサンプル サイズを決定する

信頼度

『あるサンプル サイズが より大きな母集団を正確に反映する 確率のこと』

これは、他のものに対する信頼と 同じように考えることができます。 何か、あるいは誰かを信頼できると どれだけ強く思えるか、ということです。 99% の信頼度を得られたら理想的です。 しかし、ほとんどの業界では、 少なくとも信頼度が 90% か 95% あればよいとされています。

• 製薬業界などでは、 サンプル サイズを使用する場合 可能な限り高い信頼度を 求めるのが普通です。 これは、医薬品をテストし それが誰にとっても効果的で安全だと 確認する必要があるためです。
• その他の研究では テストや調査の結果が 正しい方向に向かっていることを 確認するだけでよい場合もあります。 例えば、塗料会社が 新色をテストする場合 信頼度は低めでも構いません。

誤差の範囲

『サンプルの結果が 実際の母集団の結果と異なることが 許容される 最大値のこと』

これは、サンプル サイズの結果が母集団全体を 使用した場合の結果に どの程度近いかを示すものです。

表計算ツールを使って計算してみる

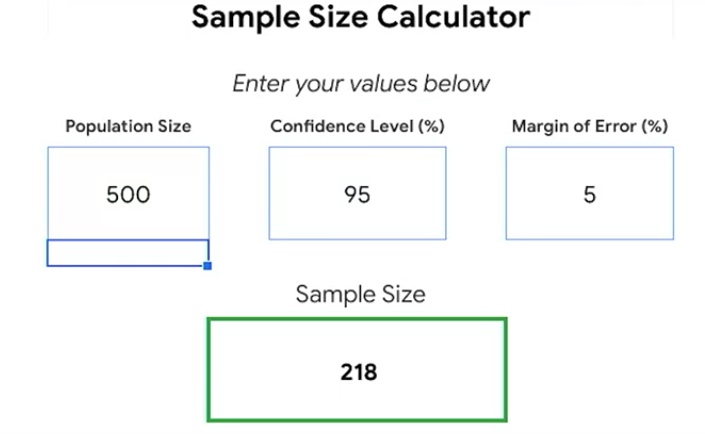
ある中学校の校長先生が 生徒達の好きなお菓子について 調査したいと言ってきたとします。 彼らは適切な サンプル サイズを、 今すぐ知る必要があります。 この学校の生徒数は 500 人、 信頼度は 95%、 誤差の範囲は 5% であるよう依頼されました。 そこで、表計算ソフトで計算します。 この手の計算ツールはインターネットで 「サンプル サイズ　計算ツール」と 検索すれば簡単に見つかります。 これらの計算ツールも 表計算ソフトの計算ツールも サンプル サイズを算出するための 複雑な計算は表示しません。

• Googleスプレットシートによるサンプルサイズ計算ツール

さっそく、母集団 500、 信頼度の割合を 95、 誤差の範囲を 5 と入力すると、 結果は約 218 となります。 つまり、先ほどの調査の場合では 適切なサンプル サイズは 218 となります。もし、218 人の生徒を調査して 55% の生徒がチョコレートを好む、 とわかったら、 500 人の生徒全員に関して それが真実である、と確信できるのです。 信頼度 95%、誤差の範囲 5% という 基準で考えると、218 人が 調査に必要な最小限の人数であると 言えることになります。

念のため申し上げますが 信頼度と誤差の範囲は 合計が 100% である必要はありません。 これらはそれぞれ、独立しているのです。 そこで、誤差の範囲を 5% から 3% に 変更してみるとします。 すると、より母集団を反映した 調査結果を得るには、 サンプルサイズを 218 から 341 に 大きくする必要があると わかります。

サンプル サイズ計算ツール

用語と定義

用語	定義
母集団	調査の対象となるグループ全体。例えば、あなたの会社の人たちを対象に調査を行う場合、母集団はあなたの会社の全従業員となります。
サンプル	データ分析において、母集団全体から抽出した一部のセグメントのこと。料理でいう試食のようなものです。会社が大きすぎて、一人ひとりを調査できない場合、母集団の代表サンプルを調べることで対応できます。
誤差の範囲	サンプルの結果が実際の母集団の結果と異なることが許容される最大値のこと。サンプルは母集団を代表するものであるため、サンプルの結果は母集団全体を調査した場合の結果とは異なる場合があります。この差を誤差といいます。誤差が小さいほど、サンプルの結果は母集団全体を調査した場合の結果に近くなります。
信頼度	あるサンプル サイズがより大きな母集団を正確に反映する確率のこと。調査結果がどの程度信頼できるかを示します。たとえば、信頼度 95% とは、同じ調査を 100 回実行した場合、その 100 回のうち 95 回は同じような結果が得られるという意味です。信頼度は、調査終了時の誤差の大きさに影響するため、調査を開始する前に目標とすべきものです。
信頼区間	統計的推定値が母集団をどの程度反映できているかを示す値の範囲のこと。この範囲は、サンプル結果 ± 誤差になります。
統計的有意性	そのサンプル結果が無作為の偶然ではないという確率のこと。有意性が大きければ大きいほど、偶然による結果は少なくなります。