はじめに
本記事は、Googleデータアナリティクスのプロフェッショナル認定証のプログラムより、参照させて頂いています。興味を持った方は、是非受講してみてください。

データの信頼性を評価する
データアナリストとして、 テストや調査を行う前に、
- サンプル サイズ
- 信頼度
- 誤差の範囲
などの 変数を把握することは重要なことです。
これは、結果が客観的であることを確認する ベストな方法であり、統計的に有意な結果を 得られる可能性が高くなります。 しかし、分析すべき調査結果がすでに 手元にある場合など サンプル サイズが分かっている場合は 自分で誤差の範囲を計算できます。 そうすれば、サンプルと母集団の間に どれくらいの差があるのか よりよくわかるようになります。
『誤差の範囲とは、サンプルの結果が 実際の母集団の結果と 異なることが許容される最大値』
母集団全体を調査したり テストしたりするのは素晴らしいですが、 通常は不可能、または非現実的です。 そこで代わりに、大きな母集団から サンプルを取ります。サンプルに基づいた誤差の範囲は 母集団全体を調査した場合と比較して 結果がどの程度異なるかを示します。
誤差の範囲は、仮説検証で得られた データがどの程度信頼できるかを 理解するのに役立ちます。 誤差の範囲がゼロに近ければ近いほど サンプルから得られる結果は 母集団全体から得られるものと一致します。
例えば、 全国からサンプルを集め 調査を行うとしましょう。 週 5 日勤務の人に、週 4 日勤務の導入を 希望するか尋ねるとします。 すると、60% の人が週 4 日勤務を 希望しているとわかりました。 誤差の範囲は 10% で、 50% から 70% の人がこの案に 賛成だということになります。 ということは、もし全国の 週休 2 日制の労働者にアンケートをとれば 50〜70% の人がこの結果に 賛成するということです。
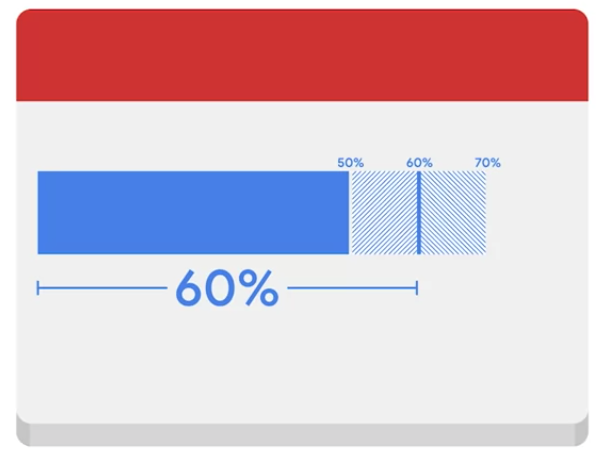
この 50〜70% という幅に着目してください。 調査結果の 60% から誤差の範囲分が 増減してカウントされるためです。 信頼度を 95% を設定していた場合 95% の確率で、母集団全体の回答のうち 50~70% が、週 4 日勤務に賛成する、 ということを指します。50% という数字と誤差の範囲が重なるので 「国民は週 4 日勤務を望んでいる」と 断言することはできません。 この場合、この調査は結論が 出なかったと言わざるを得ません。
もし、より少ない誤差の範囲、 例えば 5% にしたいとき、つまり 55% から 65% までにおさめたければ サンプル数を増やせばよいでしょう。 サンプル サイズがすでに確定している場合は 自分で誤差の範囲を計算できます。
そして、その誤差の範囲に基づいて 結果が統計的に有意である可能性が どの程度あるか、自分で判断できます。 一般的に、アンケートに参加する人数が 多ければ多いほど、サンプルが 母集団全体を反映している可能性が上がります。
信頼度を下げることも 同じ効果をもたらしますが それは皆さんの調査が正確である可能性を 低くすることにもなります。つまり、誤差の範囲を計算するには
- 母集団のサイズ
- サンプル サイズ
- 信頼度
の 3 つが必要なのです。
サンプル サイズの時と同様、 「誤差の範囲 計算」で検索すると、 たくさんの計算ツールがオンラインにはあります。
たとえば、新薬の有効性に関する 研究を行っているとします。 世界人口の 1% が罹患している 疾患を持つ 500 人の被験者を サンプルとします。 約 8,000 万人の母集団が 研究対象です。薬の研究ですから、信頼度は 99% である必要があります。 また、誤差の範囲も 小さくする必要があります。 早速、計算してみましょう。
スプレッドシートの該当セルに 母集団、信頼度、そして サンプルサイズの数字を入れます。 その結果、誤差の範囲は ±約 6% になります。 治験が完了したら、その結果に 誤差の範囲を当てはめて 結果がどの程度信頼できるかを 判断します。

データ完全性を確認し、 データと目的を一致させることで 良い状態で分析を完了できることも 覚えておくとよいでしょう。
誤差の範囲を計算するツール