R クラスタ分析

はじめに

個人の勉強用に制作しました．

クラスタ分析

p個の変数を持つ，n個の対象(object)を似たものが同じクラスになるように分類するのがクラスタ分析である．

i) 階層的方法
階層的方法は各個体からそれぞれの個体までのすべての距離を計算して，併合または分割によってクラスタを形成していく．併合過程では、1つの個体を1つのクラスターとするところから始まって，最終的にn個の個体全体で1つのクラスターとするところまで階層的に進んでいく．分割過程はこれとはまったく逆の方法でクラスターを分割していく．

ii) 非階層的方法
最初にクラスタの数を与え，適当なクラスタの中心を与えて
これに個体を入れたり出したりしてクラスタを形成していく方法である．

階層的方法.R

X = c(1,2,3,7,8,9)
Y = c(3,2,4,9,7,9)
m.data = data.frame(x=x, y=y)
m.dist = dist(m.data, method = "euclidean") #距離を計算 #dist関数
m.clust = hclust(m.dist, method = "single") #クラスタの形成　#hclust関数
plot(m.clust)
dend = as.dendrogram(m.clust) #as.dendrogram関数 #具体的な数値を確認したい
str(dend) #str関数
h3 = cutree(m.clust, h=3) #h=3で分割 #cutree関数
h2 = cutree(m.clust, h=2) #h=3で分割

非階層的方法.R

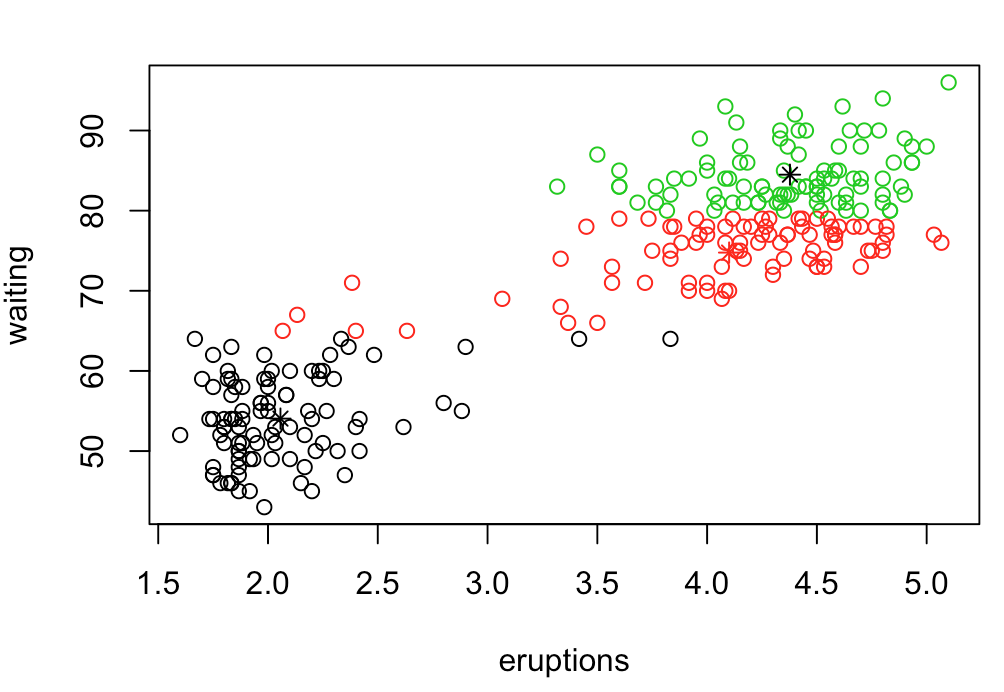
c1 = kmeans(m.data, 2) #k-means関数
plot(m.data, col=c1$cluster) #kmeansの結果を色分けして表示
points(c1$centers, col=1:2, pch=8) #各クラスタの代表点を*で表示
head(cosmetics)

d.cosme = dist(cosmetics, method = "euclidean") #dist関数
c.cosme = hclust(d.cosme, method = "single") #クラスタの形成
plot(c.cosme)

練習問題

大問1

次々と近郊のデータを統合してクラスタが形成される「鎖効果」が発生．
これを回避するにはウォード法を用いると良い.(距離の定義を実用的なウォード法に変える)

ウォード法.R

d.cosme = dist(cosmetics, method = "euclidean") #dist関数
C.cosme = hclust(d.cosme, method = "ward.D") #ウォード法
plot(C.cosme)

dend = as.dendrogram(c.cosme)
str(dend)

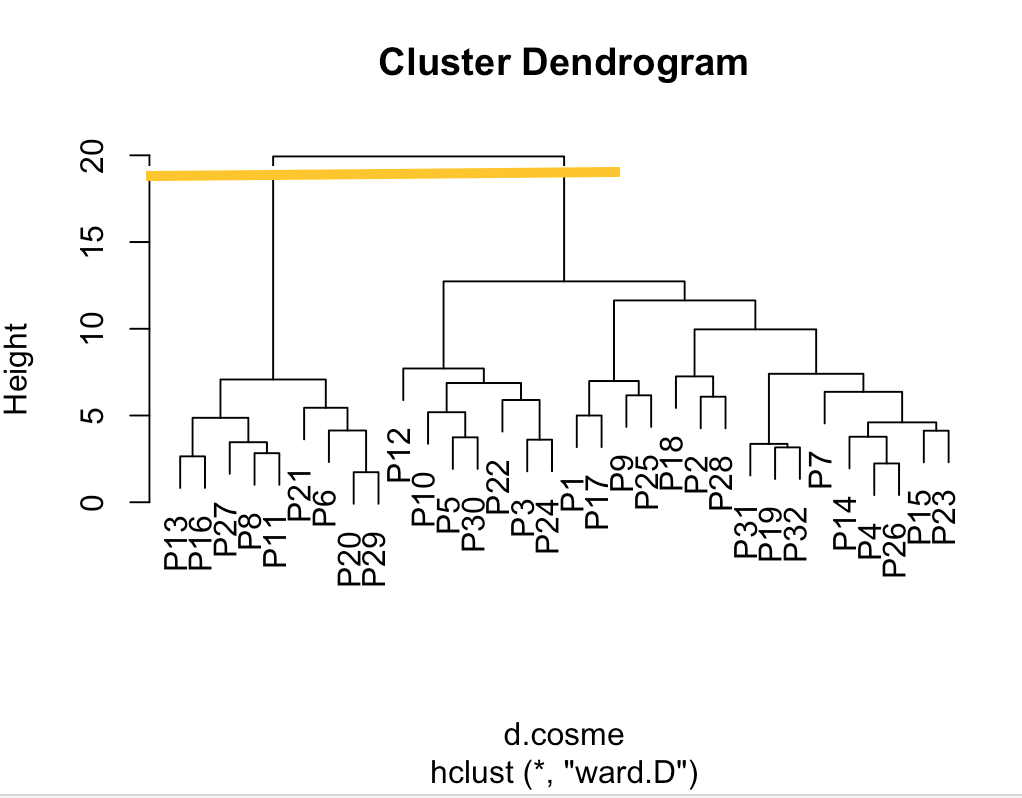
○ データを持ちに被験者を2グループに分ける場合，どれぐらいの距離で分けるのが良いか

• ウォード法を用いた樹形図のグラフを確認すると，以下のようになるため，20に近い距離の値で分類するのが良い．
• (3つに分類する場合は約12前後の値)

大問2

kmeans法.R

head(iris)　#データをセット #irisはもともとRにあるデータ
my.iris = iris[,2:3]　#必要なデータのみ取り出す
plot(my.iris, col=iris[,5])　#3色に分けて表示
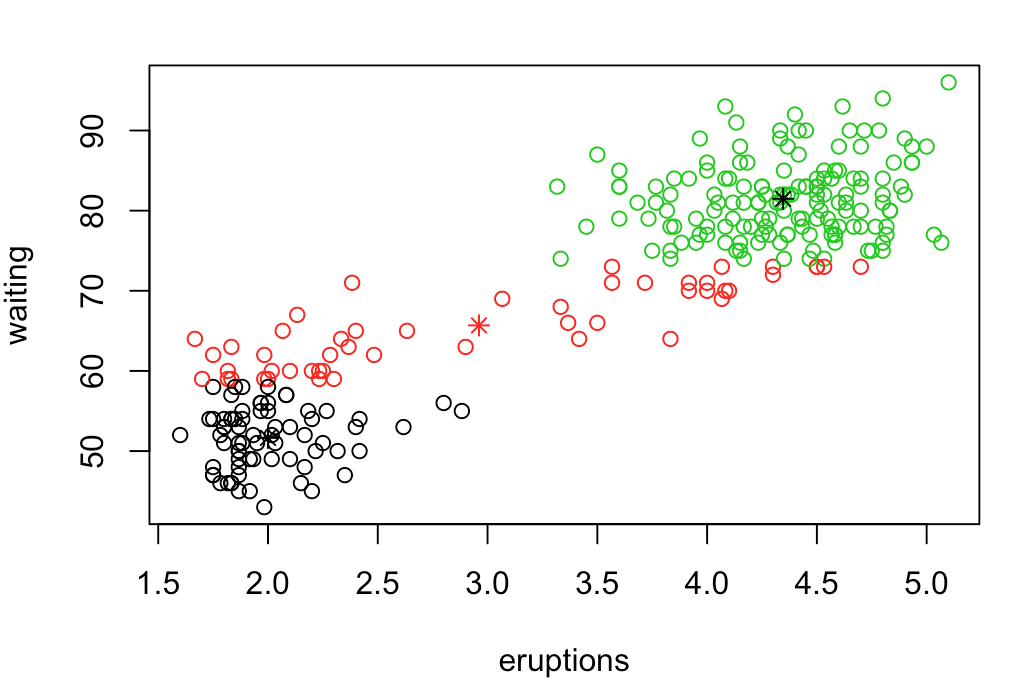
k3 = kmeans(faithful, 3)$cluster #k=3でクラスタリング #kmeans法
plot(faithful,col=k3)#3色に分けて表示

1. 今回の分析だと，irisのデータから，クラスタの中心点を３つ打たれる
2. 全てのデータからもっとも近くにある中心点のクラスタが割り当てられる
3. 分類されたクラスタ内のデータの平均値を新たなクラスタの中心点にする
4. 2に戻る

のようにクラスタを割り当てるための中心点が徐々に正しい位置へ収束していく構造になっているため，複数回分析を行う必要がある．