はじめに
近年、グラフデータに対してディープラーニングを適用しようとする、いわゆるGraph Neural Networks(GNN)と呼ばれる研究領域が、一部のコミュニティで注目されています。GNN系の手法は、グラフデータを対象としたクラス分類やリンク予測、クラスタリングなどの様々なタスクにおいて優れた成果を達成しています。
そして、企業が蓄積している多くのデータは、実はグラフ構造を含んでいます。ソーシャルネットワークのような明確なものだけではなく、購買ログや商品閲覧ログも、ユーザと商品を結ぶ2部グラフです。当社の場合も会計データを扱っており、これは企業側ノードと勘定科目側ノード、そして金額がエッジの重みとして表現される、重み付き2部グラフとして表現可能です。
また、私の経験上、データ解析業務では異種グラフデータ、すなわち異なる種類のデータで構成されているグラフ、を対象としたタスクに取り組むことがよくあります。「優良顧客はどのような商品を買っており、どのような属性に該当するか」といった横断的な分析を行ったり、商品の閲覧、購買ログや顧客属性を統合的に活用した商品推薦システムを作ったり、といった感じです。私は最近、このような異種グラフをうまく取り扱うことができる、より良い手法を日々模索しています。
今回は、その中で出会ったGNN系手法の1つとして、2019年5月にサンフランシスコで開催されたThe Web Conference (WWW)にて報告された、異種グラフを対象とした分類モデル構築手法の1つであるHeterogeneous Graph Attention Network (HAN)を簡単に紹介したいと思います。コードはこちらで公開されています。有難いですね。
HANの選定理由は、比較的筋が良い汎用的な手法だと感じたこと、そしてまだ日本語での解説記事が(たぶん)存在しないためです。決して異種グラフに対する分類はHANだけで十分であると主張しているわけではないことに注意してください。実務での応用の際は、データ及び手法の性質を踏まえ、しっかりと比較検討を行なうことをオススメします。
Heterogeneous Graph Attention Network (HAN)
HANは、単一のグラフデータに対する教師あり学習手法であるGraph Attention Networks (GAT)を、異種グラフに対して拡張した手法の1つです。GATはその名の通り、self-attention戦略に従い、グラフ内の各ノードの潜在表現を近隣ノードに注意しながら学習していきます。ベンチマークデータを使用したtransductiveおよびinductive学習タスクにおいて2018年当時の最先端の成果を達成し、GNN系で注目されている手法の1つです。
GATの異種グラフ拡張をテーマとした研究は、同時期にいくつか報告されています。HANが報告されたWWW2019でもたしか3件ほど採択されていましたし、KDDやその他トップカンファレンスでもそれっぽいものをちらほら見かけました。これらの全ての文献を読み込んだわけではないですが、アプローチはどれも比較的似ているなという印象です。どの手法が一番優れているのか、という議論はここでは控えます。
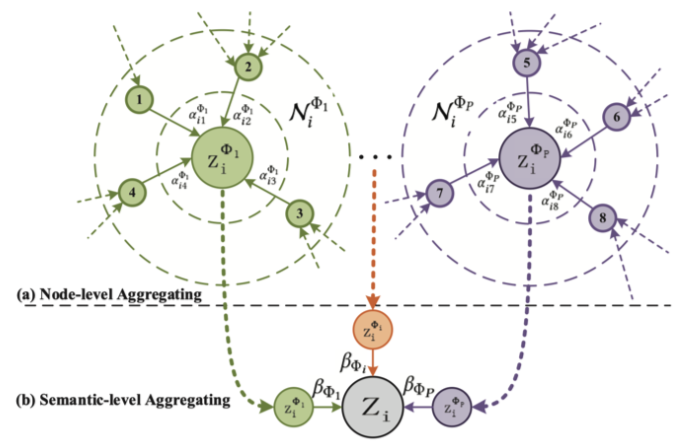
HANでは、Node-level AttentionとSemantic-Level Attentionと呼ばれる、2つのAttentioinを実装しています。まず、Node-level Attentionとして、ノードとメタパスベース近傍の重みを学習し、その後Semantic-Level Attentionとして、メタパスの重要性を学習します。アウトプットである潜在表現は、2つのレベルのAttentioin値に基づいて、階層的な方法で近傍から特徴を集約することにより生成されます。HANモデルは、end-to-endでバックプロパゲーションによって最適化されます。
下図がHANの全体像です(論文より引用)。
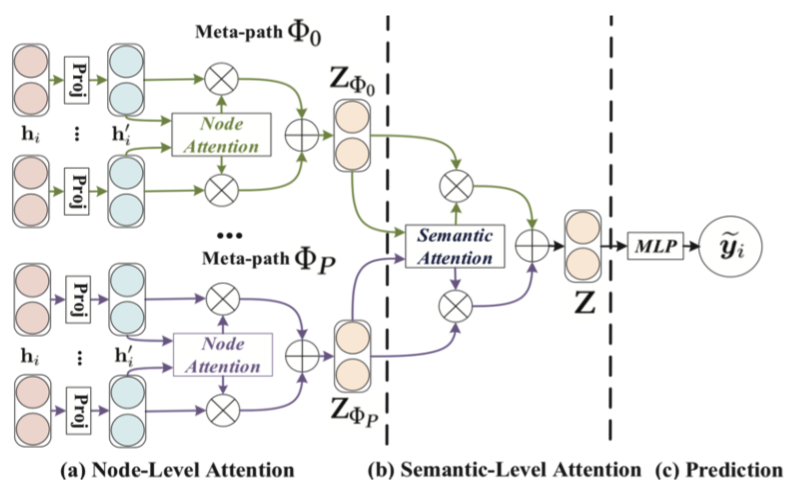
以下で、用語の定義と2つのAttentionを順に説明していきます。
用語の定義
論文で説明に使用されていた図を用いて、グラフや用語の定義を行なっていきます。
まず、異種グラフは$G = \{V, E\}$で定義されます。$V$はノード集合、$E$はエッジ集合です。
下図は、異種グラフの例として論文で紹介されている、映画関連グラフのイメージです(論文より引用)。
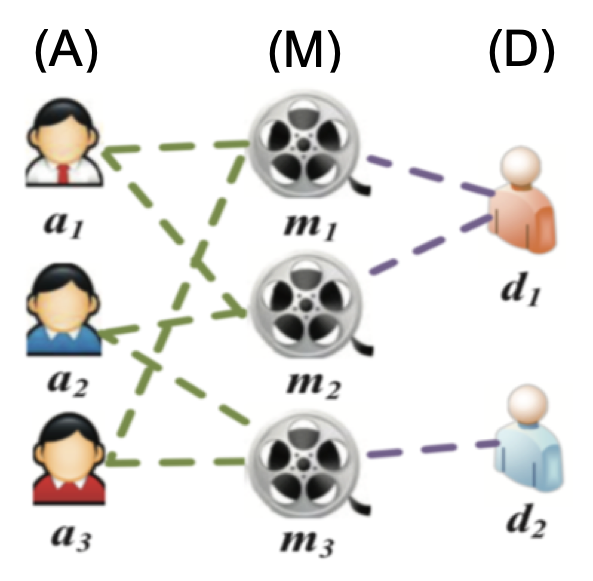
図では、ノードタイプとしては俳優(A)、映画タイトル(M)、映画監督(D)の3種類が存在します。エッジは、映画と出演俳優を表すエッジ(AとMの接続)と、映画と制作監督を表すエッジ(MとDの接続)の2種類です。
メタパス$\Phi$は、2つのオブジェクトを接続する複合関係です。上図では、ある2つの映画は、複数のメタパス(M-A-MとM-D-M)を介して接続でき、$\Phi$に応じて異種グラフのノード間の関係は異なる意味を持ちます。すなわち、共演者の関係は、M-A-Mによって明らかにすることができますが、M-D-Mは、同じ監督によって制作されることを意味します。
$\Phi$が与えられると、各ノードのメタパスベース近傍集合が存在します。メタパスベース近傍$N_{i}^{\Phi}$は、メタパス$\Phi$のあるノード$i$の近傍($i$を含む)を意味します。例えば、メタパスM-A-Mにおける$m_1$のメタパスベース近傍は、$m_1, m_2, m_3$となり、メタパスM-D-Mにおける$m_1$のメタパスベース近傍は$m_1$と$m_2$です。
Node-level Attention
Node-level Attentionは、メタパスベース近傍の重みを学習し、それらを集約してノードの埋め込みを取得します。まず、異なる型のノード特徴を同じ特徴空間に射影するように、型固有の線形写像を行います。
$$h_{i}^{\prime} = M_{\Phi_{i}} \cdot h_{i}$$
$M_{\Phi_{i}}$は型固有の変換行列です。
メタパス$\Phi$を介して接続されているノード対$(i, j)$が与えられると、ノード$i$にとってのノード$j$の重要度$e_{i j}^{\Phi}$を以下の式で学習します。
$$e_{i j}^{\Phi} = att_{node}(h_{i}^{\prime}, h_{j}^{\prime} ; \Phi)$$
ここで、$att_{node}$はNode-level Attentionを行うディープニューラルネットワークを表します。$att_{node}$はすべてのメタパスベースのノード対に共有されます。これは、1つのメタパスに類似の接続パターンが存在するためです。
$e_{i j}^{\Phi}$を得た後は、ソフトマックス関数を介してそれらを正規化した重み係数$\alpha_{ij}^{\Phi}$を計算します。$\sigma$は活性化関数を表し、||は連結演算を表します。
$$\alpha_{ij}^{\Phi} = softmax(e_{i j}^{\Phi}) = \frac{\exp(\sigma(a_{\Phi}^{T} \cdot [h_{i}^{\prime} || h_{j}^{\prime}]))} {\sum_{k \in N_{i}^\Phi} \exp(\sigma(a_{\Phi}^{T} \cdot [h_{i}^{\prime} || h_{k}^{\prime}]))}$$
次に、隣接する特徴$h_{j}^{\prime}$と、それに対応する係数$\alpha_{ij}^{\Phi}$を用いて、メタパスベースのノードiの埋め込み$z_{i}^{\Phi}$を以下の式で導きます。
$$z_{i}^{\Phi} = \sigma(\sum_{j \in N_{i}^{\Phi}} \alpha_{ij}^{\Phi} \cdot h_{j}^{\prime})$$
Semantic-level Attention
$z_{i}^{\Phi}$はメタパスごとに生成されるので、これだけでは単一のグラフの情報しか取り込めません。より包括的なノード埋め込みを学ぶために、全てのメタパスから得られる情報を融合することが望ましいです。ただし、一般的に、ある特定のタスクにおけるメタパスの重要性は異なります。このメタパス自体の重要度を自動で学習するために、Semantic-Level Attentionを導入します。
まず、非線形変換(例えば、1層MLP)を介して$z_{i}^{\Phi}$を変換します。それから、Semantic-Level Attentionベクトル$\mathbf{q}$とともに、変換された埋め込みの類似度としてノードレベル埋め込みの重要度を測定します。さらに、各メタパスの重要度として説明可能な全てのノードレベル埋め込みの重要度を平均します。$w_{\Phi_{i}}$として表される各メタパスの重要度は以下の式で定義されます。
$$w_{\Phi_{i}}=\frac{1}{|\mathcal{V}|} \sum_{i \in \mathcal{V}} \mathbf{q}^{\mathrm{T}} \cdot \tanh \left(\mathbf{W} \cdot z_{i}^{\Phi}+\mathbf{b}\right)$$
ここで、$\mathbf{W}$は重み行列、$\mathbf{b}$はバイアスベクトルです。有用な比較のために、上記全てのパラメータは、全てのメタパスとノードレベル埋め込みで共有されます。
各メタパスの重要度を得た後、それらはsoftmax関数によって正規化されます。
$$\beta_{\Phi_{i}}=\frac{\exp \left(w_{\Phi_{i}}\right)}{\sum_{i=1}^{P} \exp \left(w_{\Phi_{i}}\right)}$$
これは特定のタスクに対するメタパス$\Phi_{i}$の寄与度として解釈することができます。$\beta_{\Phi_{i}}$が高いほど、より重要なメタパスであることを意味します。
最終的な埋め込み$Z$は、$\beta_{\Phi_{i}}$を係数として、ノードレベル埋め込みを集約することで取得されます。
$$Z = \sum_{i=1}^{P} \beta_{\Phi_{i}} \cdot Z_{\Phi_{i}}$$
所感
論文を読んだ感想を述べると、まず、個人的に感じたこの手法の最大の利点は、解釈可能性の高さかなと思います。end-to-endなモデルなので、異なるメタパスに存在するエッジの重要度を同じ尺度で測ることができ、色々捗りそうです。ただし、実験結果を見ると、Semantic-Level Attentionの効果が限定的であることが気になりました。直感的には、ちゃんと学習できていれば、もう少し大きな効果があっても良いのかなとは思ったのですが。使用したデータセットやタスクとの相性が悪かっただけの可能性も考えられます。理論的には、メタパス間の重要度が同等である場合や、メタパス同士が予測性能の観点で補完関係にない場合は、Semantic-Level Attentionは効果がないので、そういった類の問題なのかもしれません。また、似たような話ですが、Semantic-Level Attentionとは、要はAttentionメカニズムによりGATモデルをアンサンブル結合していると解釈できるので、代表的なスタッキング手法との比較検証もやってほしかったなと思いました。まぁ、どこまでを比較手法とするかは難しいのですが。。。自分で論文を書く際にもとても悩むところです。
今回は、時間の関係でHANの簡単な論文解説にとどめましたが、次はGNN系やNetworkEmbeddings系のアルゴリズムの実装方法やオープンソースコードの動かし方なども記事にできれば良いなと思っています。