【Python】BFS、DFS、ダイクストラ法、01BFSを最小変更で書き分ける方法【競プロ】

はじめに

みなさんこんにちは、まぬおです。
今回はBFS、DFS、ダイクストラ、01BFSをコードの一部を変えるだけで実現する方法を紹介します。

それぞれのアルゴリズムを簡単に紹介

こちらのグリッドをつかって説明します。
白が通れるところです。

BFS

BFSは幅優先探索というもので、スタートに近いものから順番に探索していくアルゴリズムです。
近いものから距離を確定させていくことが出来るので、最短経路を求める問題でよく使用します。

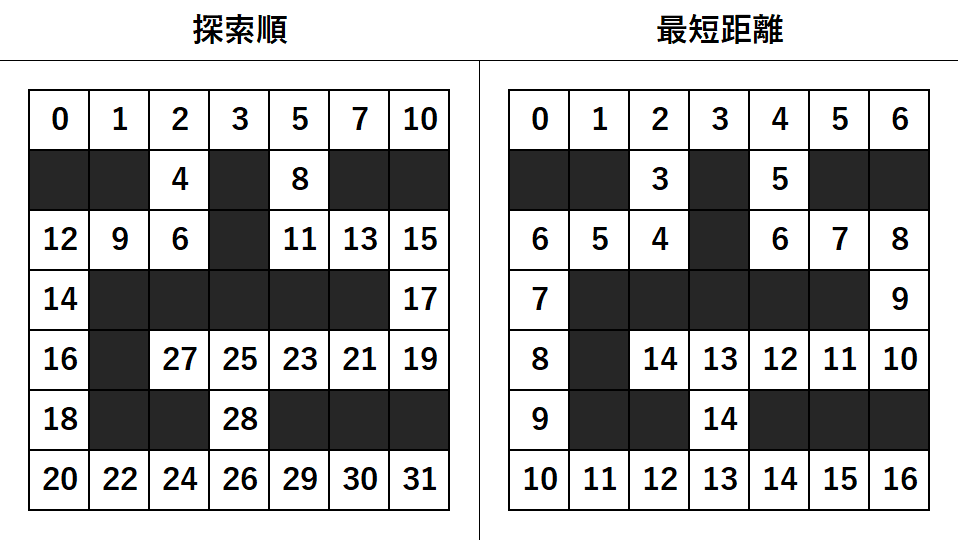
左は探索順で、右が探索の結果計算されたスタートからの最短距離です。
ゴールの最短は16マスであることが計算できました。
近い順に探索するので同じマスを探索することなく、無駄なく探索が出来ます。

DFS

DFSは深さ優先探索というもので、行けるところまで探索して無理だったら戻ってくるというアルゴリズムです。
行ける限り探索しますので、今回のようにループが盤面にあると同じマスを複数回探索することになります。
ですので最短経路を求める問題には不向きですが、ループ検出などDFSが得意な状況も多くあります。

図は探索途中の結果です。
26まで探索し、次のマスは2番目に探索した箇所なのでこれでループを検出することが出来ました。

ダイクストラ法

ここで、マスにコストを導入するとどうなるでしょうか？
DFSまでは次のマスへ移動するコストは等価でしたが、コストが導入されると距離上では近くてもコスト上では遠くなることがあり得ます。

コストが導入された時に活躍するのがダイクストラ法です。
マス目のコストの小さい順に探索し、コストを確定させていきます。

コスト無しの時に通った道のコストが高くなり、距離上では回り道の方がコストが低くなりました。
ゴールのコストは18です。

01BFS

ここでコストを無くしてマス目に柵を置いてみましょう。"#"が柵の位置です。
柵は越えられますができるだけ少ない数にしたいです。
どうしたらいいでしょうか？

実はこの問題は柵の位置をコスト1とすることでダイクストラでも解けます。
しかし、BFSを応用した01BFSを使うとより計算量を少なくできます。

ゴールまでに最低3つ柵を越えなければいけません。

実装のイメージ

ここからは実際の実装をする際のイメージを紹介します。

BFS

BFSを実装する時は後入れ先出しのキューを使用します。
Pythonでは具体的に、dequeのpopleftとappendを使用します。
今計算しているマスの隣のマスをキューの一番最後に持ってくることで、まだ計算していない同じ距離のマスを先に計算します。

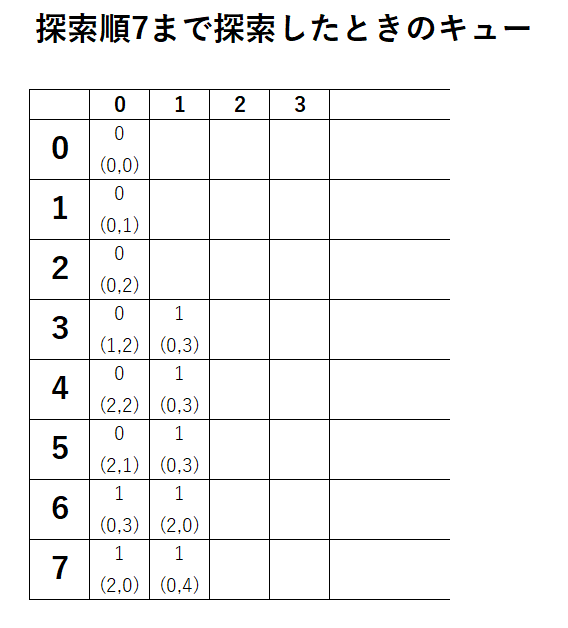
• スタートの (0, 0) を探索し、隣の (0, 1) を末尾に追加
• (0, 1) を探索し、隣の (0, 2) を末尾に追加
• (0, 2) を探索し、隣の (0, 3) と (1, 2) を末尾に追加
• (0, 3) を探索し、隣の (0, 4) を末尾に追加
• (1, 2) を探索し、隣の (2, 2) を末尾に追加
  ...

キューへの追加順に探索していることがわかります。

DFS

DFSを実装する時は先入れ先出しのキューを使用します。
これはlistのpopとappendで実現できます。
もちろんdequeでも実装できますが、計算量は増えます。
また、再帰で実装する方法もありますが、Pythonでは計算時間がキューより増えてTLEになる場合がありますのでキューで実装するのをおすすめします。

• スタートの (0, 0) を探索し、隣の (0, 1) を先頭に追加
• (0, 1) を探索し、隣の (0, 2) を先頭に追加
• (0, 2) を探索し、隣の (1, 2) と (0, 3) を先頭に追加
• (1, 2) を探索し、隣の (2, 2) を先頭に追加
• (2, 2) を探索し、隣の (2, 1) を先頭に追加
  ...

(0, 2) 探索時に追加した (0, 3) が後回しにされていることがわかります。

ダイクストラ法

ダイクストラ法では追加した順に関わらず、コストの順に探索します。
キューの中身をコスト順に並び替えることが必要ですが、そういう時に使えるのが優先度付きキューです。
Pythonではheapqを使用します。

• スタートの (0, 0) を探索し、コスト1の(0, 1) をキューに追加
• (0, 1) を探索し、コスト2の(0, 2) をキューに追加
• (0, 2) を探索し、コスト5の(1, 2) とコスト3の(0, 3) をキューに追加
• (0, 3) を探索し、コスト4の(0, 4) をキューに追加
• (0, 4) を探索し、コスト5の(1, 4) とコスト5000兆4の(0, 5) をキューに追加
  ...

先に追加された (1, 2) がコストの大小で (0, 4) に追い抜かされています
BFSと同様に探索したマスはコストが確定しているので効率よく探索出来ます

01BFS

01BFSは言うなれば前述の三つのハイブリッドです。
隣のマスがコスト0で行けるならDFSのように先頭に追加し、コスト1かかるならBFSのように末尾に追加して後回しにします。
先頭と末尾に追加する必要があるのでBFSと同じくdequeを使用します。

なぜ優先度付きキューが必要ないか

変数$m$, $M$, $x$を以下のように定義します

• $m$：キュー内のコストの最小値
• $M$：キュー内のコストの最大値
• $x$：新しく追加するコスト

ダイクストラ法では要素の追加時に($m<x<M$)となる場合があります。
キューの中の適切な位置に挿入するためには優先度付きキューを使用する必要があります。

しかし、01BFSの場合は$m$と$M$の差は高々1です。
キューの要素は高々2種類になりますので、($x=m$)または($x=M$)が成り立ちます。
前述のように追加する箇所を適切に選ぶことでキューがソートされた状態を維持できるため、優先度付きキューは必要ありません。

優先度付きキューを使用していませんが、コストの低い順に探索できています

実際に実装してみた(Python)

ここからは具体的なコードを例示します

BFS

入力を以下とした時にBFSを使用して最短距離を求めるコードを紹介します

$H\hspace{5pt} W$
$S_1$
$S_2$
$\cdots$
$S_H$

• $S_i$は各文字が#または.である長さ$W$の文字列

入力例

7 7
.......
##.#.##
...#...
.#####.
.#.....
.##.###
.......

コード例

from collections import deque

# 入力
H, W = map(int, input().split())
S = [input() for _ in range(H)]

# スタートとゴールを設定
s, g = (0, 0), (H-1, W-1)

# 最短距離をメモする変数
memo = [[-1]*W for _ in range(H)]

# スタートを0に
memo[s[0]][s[1]] = 0

dir = [(0, 1), (0, -1), (1, 0), (-1, 0)]

# スタートを最初に挿入
q = deque([s]) # キュー：[(0, 0)]
while q:
    i, j = q.popleft() # キューの左から見る
    for d in dir:
        ni, nj = i+d[0], j+d[1]
        if 0 <= ni < H and 0 <= nj < W:     # 添え字が不正でない
            if S[ni][nj] == "#": continue   # 壁
            if memo[ni][nj] != -1: continue # 確定済み
            # 現在+1をメモ
            memo[ni][nj] = memo[i][j]+1
            # キューの右に追加
            q.append((ni, nj))

# ゴールの距離を取得
ans = memo[g[0]][g[1]]
print(ans)

dequeを使用し、左から出して右から入れています
処理を一般化すると以下です

from collections import deque

q = deque([{最初の要素}]) # dequeを使用
while q:
    {今の要素} = q.popleft() # キューの左から見る
    for {次の要素を列挙するfor文} :
        if {次の要素が不正でない場合} :
            {次の要素に対する処理}
            q.append({次の要素}) # キューの右に追加

この一般化されたコードをベースに最小変更していきます

DFS

DFSは先入れ先出しで、popとappendが出来れば実装できるのでlistで十分です。

q = [{最初の要素}] # listを使用
while q:
    {今の要素} = q.pop() # キューの右から見る
    for {次の要素を列挙するfor文} :
        if {次の要素が不正でない場合} :
            {次の要素に対する処理}
            q.append({次の要素}) # キューの右に追加

実はこれだけでBFSからDFSに変更することが出来ました。
変更箇所は以下の二行のみです。
計算量が気にならないならdequeのままでも良いと思います。

- q = deque([{最初の要素}]) # dequeを使用
+ q = [{最初の要素}] # listを使用
  while q:
-    {今の要素} = q.popleft() # キューの左から見る
+    {今の要素} = q.pop() # キューの右から見る
     for {次の要素を列挙するfor文} :
         if {次の要素が不正でない場合} :
             {次の要素に対する処理}
             q.append({次の要素}) # キューの右に追加

DFS自体はこのコードで実現できていますが、実は問題があります。
この問題については後述します。

ダイクストラ法

ダイクストラ法は優先度付きキューheapqを使用するのでした。
以下を入力とした時に最小コストを求めるコードを紹介します。

$H\hspace{5pt}W$
$S_1$
$S_2$
$\cdots$
$S_H$
$C_{1,1}\hspace{5pt}C_{1,2}\hspace{5pt}\cdots\hspace{5pt}C_{1,W}$
$C_{2,1}\hspace{5pt}C_{2,2}\hspace{5pt}\cdots\hspace{5pt}C_{2,W}$
$\cdots$
$C_{H,1}\hspace{5pt}C_{H,2}\hspace{5pt}\cdots\hspace{5pt}C_{H,W}$

• $S_i$は各文字が#または.である長さ$W$の文字列
• $C_{i,j}$ は $i$行$j$列のマスのコスト

入力例

7 7
.......
##.#.##
...#...
.#####.
.#.....
.##.###
.......
1 1 1 1 1 5000000000000000 1
0 0 3 0 1 0 0
3 3 3 0 1 1 1
3 0 0 0 0 0 1
3 0 1 1 1 1 1
3 0 0 1 0 0 0
3 3 3 1 1 1 1

5000兆を普通に入力できるのはPythonのごり押しです(C++ではlong longを使用してください)

コード例

from heapq import heappop, heappush

# 入力
H, W = map(int, input().split())
S = [input() for _ in range(H)]
C = [list(map(int, input().split())) for _ in range(H)]

# スタートとゴールを設定
s, g = (0, 0), (H-1, W-1)

# 最短距離をメモする変数
memo = [[-1]*W for _ in range(H)]

dir = [(0, 1), (0, -1), (1, 0), (-1, 0)]

# スタートを最初に挿入
q = [(0, s[0], s[1])] # キュー：[(0, 0, 0)]
while q:
    cost, i, j = heappop(q) # 優先度付きキューから取り出し
    if memo[i][j] != -1: continue # 確定済み
    memo[i][j] = cost # 確定した要素をメモ
    for d in dir:
        ni, nj = i+d[0], j+d[1]
        if 0 <= ni < H and 0 <= nj < W:     # 添え字が不正でない
            if S[ni][nj] == "#": continue   # 壁
            if memo[ni][nj] != -1: continue # 確定済み
            # 次の要素のコストを計算
            ncost = memo[i][j] + C[ni][nj]
            heappush(q, (ncost, ni, nj)) # 優先度付きキューに挿入
            
ans = memo[g[0]][g[1]]
print(ans)

heapqを使用してコスト順に取り出しています
一般化すると以下になります

from heapq import heappop, heappush

q = [({最初の要素のコスト}, {最初の要素})] # listを使用し、コストを含める
while q:
    {今の要素のコスト}, {今の要素} = heappop(q) # 優先度付きキューから取り出し
    if {要素が確定していた場合} : continue
    {確定した要素に対する処理}
    for {次の要素を列挙するfor文} :
        if {次の要素が不正でない場合} :
            heappush(q, ({次の要素のコスト}, {次の要素})) # 優先度付きキューに挿入

コストを一番目に含めたtupleを優先度付きキューに入れることによって、コスト順に取り出せます
BFSと違う点は、次の要素をキューに追加する時点では追加するコストが最善とは限らない点です

例えば(6, 0) のコスト24のマスですが、このマスは (6, 1) から来たコスト24の場合と (5, 0) から来たコスト26の場合がキューに追加されます。
コストの低い24でこのマスは確定しますが、確定後に26の要素も来ますので適切に弾く必要があります。

01BFS

01BFSでは状況によって追加する先を調整して、優先度付きキューを使わずにダイクストラを行うのでした
入力を以下とした時に01BFSを使用して柵を越える数を求めるコードを紹介します

$H\hspace{5pt}W$
$S_1$
$S_2$
$\cdots$
$S_H$

• $S_i$は各文字が#、*または.である長さ$W$の文字列

入力例

7 7
...*...
##.#.##
*..#..*
.#####.
.#.*..*
.##.###
*..*...

コード例

from collections import deque

# 入力
H, W = map(int, input().split())
S = [input() for _ in range(H)]

# スタートとゴールを設定
s, g = (0, 0), (H-1, W-1)

# 最短距離をメモする変数
memo = [[-1]*W for _ in range(H)]

# スタートを0に
memo[s[0]][s[1]] = 0

dir = [(0, 1), (0, -1), (1, 0), (-1, 0)]

# スタートを最初に挿入
q = deque([s]) # キュー：[(0, 0)]
while q:
    i, j = q.popleft() # キューの左から見る
    for d in dir:
        ni, nj = i+d[0], j+d[1]
        if 0 <= ni < H and 0 <= nj < W:     # 添え字が不正でない
            if S[ni][nj] == "#": continue   # 壁
            if memo[ni][nj] != -1: continue # 確定済み
            # コストを計算
            cost = 1 if S[ni][nj] == "*" else 0
            # 次の要素のコストをメモ
            memo[ni][nj] = memo[i][j]+cost

            # コストに応じて追加
            if cost == 1:             # コストが1の場合
                q.append((ni, nj))      # 右に追加
            else:                     # コストが0の場合
                q.appendleft((ni, nj))  # 左に追加

# ゴールのコストを取得
ans = memo[g[0]][g[1]]
print(ans)

次の要素のコストに応じて追加する先を調整しています
より一般化したのが以下です

from collections import deque

q = deque([{最初の要素}]) # dequeを使用
while q:
    {今の要素} = q.popleft() # キューの左から見る
    for {次の要素を列挙するfor文} :
        if {次の要素が不正でない場合} :
            {次の要素に対する処理}
            if {コストが1の場合} :
                q.append({次の要素}) # キューの右に追加
            if {コストが0の場合} :
                q.appendleft({次の要素}) # キューの左に追加                

BFSと違う箇所は追加する部分のみです。

  from collections import deque

  q = deque([{最初の要素}]) # dequeを使用
  while q:
      {今の要素} = q.popleft() # キューの左から見る
      for {次の要素を列挙するfor文} :
          if {次の要素が不正でない場合} :
              {次の要素に対する処理}
-             q.append({次の要素}) # キューの右に追加
+             if {コストが1の場合} :
+                 q.append({次の要素}) # キューの右に追加
+             if {コストが0の場合} :
+                 q.appendleft({次の要素}) # キューの左に追加    

これだけの変更で01BFSを実装出来ました。

終わりに

以上で、4種類のアルゴリズムをBFSをベースに最小変更で実装する方法の紹介を終わります。
大きな枠組みを共通させて細部を調整する方法で覚えておけば、似たアルゴリズムとして覚えられるので便利です。
この記事はARC177で 01BFS を知ったのをきっかけに執筆しました。
4つのアルゴリズムを一つにまとめるって物理の4つの力をまとめるみたいで良いですね（？
ノーベル物理学賞はボクのものです（？？？
以下は余談です。

余談。もしくは割と重要な注意点

スタック型DFSの問題

今回紹介したスタック型DFSではできないことがあります
それは次の要素を確定させた後に今の要素を確定させるという処理です
というか、DFSは普段こういうことをしたい時に使います
DFSを実装する時によく使われる再帰型ならこの処理は可能ですが、スタック型はここまでなのでしょうか？
Pythonで遅い再帰を使わざるを得ないのでしょうか？
いいえそうではありません
処理を分けることでスタック型でも実装出来ます

例題

$N$頂点の木が与えられます。根は頂点$1$です
各頂点の部分木のサイズをそれぞれ求めてください

$N$
$A_1\hspace{5pt}B_1$
$\cdots$
$A_{N-1}\hspace{5pt}B_{N-1}$

入力例

7
1 2
1 3
2 4
1 5
3 6
5 7

再帰型で実装

再帰型に屈した場合の実装は以下です

from collections import defaultdict

# 入力
N = int(input())
# 辺を格納する変数
E = defaultdict(list)
for _ in range(N-1):
    a, b = map(int, input().split())
    # 無向辺を格納
    E[a-1].append(b-1)
    E[b-1].append(a-1)

# サイズをメモする変数
memo = [-1]*N

# DFSする関数
def dfs(i):
    # 探索したので暫定サイズを1に(自分自身)
    memo[i] = 1
    # つながってる頂点を探索
    for j in E[i]:
        if memo[j] != -1: continue # すでに探索していたら親頂点
        dfs(j) # 子頂点を探索
        memo[i] += memo[j] # 子頂点のサイズを加算

# 頂点1から探索
dfs(0)

# 答えを出力
for i in range(N):
    print(memo[i])

なんてシンプルな実装なのでしょうか...(うっとり
再帰型はコードがシンプルになるのが利点です。
このままで行きたいところですが、Python競プロerは処理速度も敵ですのでスタック型にしないとTLEになる状況が良くあります。

スタック型で実装

再帰型の処理に出来てスタック型に出来ない箇所はこの部分です。

memo[i] += memo[j] # 子頂点のサイズを加算

子頂点のサイズを確定させてから親頂点のサイズに加算したいのですが、子頂点をスタックへ追加する時にはまだ子頂点のサイズが確定していないので加算できません。

そこで、処理に番号を付けて処理を分けるテクニックを使います。
具体的には、以下のように処理に番号を付けます。

• $1$ $i$：頂点$i$の子頂点を探索
• $2$ $i$ $j$：頂点$i$に頂点$j$のサイズを加算

そして、キューを処理する問題のように場合分けをします。

from collections import defaultdict

# 入力
N = int(input())
# 辺を格納する変数
E = defaultdict(list)
for _ in range(N-1):
    a, b = map(int, input().split())
    # 無向辺を格納
    E[a-1].append(b-1)
    E[b-1].append(a-1)

# サイズをメモする変数
memo = [-1]*N

# スタートを最初に挿入。処理番号は1
q = [(1, 0)]
while q:
    e = q.pop() # キューの右から見る
    # 処理1：子頂点の探索
    if e[0] == 1:
        i = e[1]
        # 探索したので暫定サイズを1に(自分自身)
        memo[i] = 1
        # つながってる頂点を探索
        for j in E[i]:
            if memo[j] != -1: continue # すでに探索していたら親頂点
            q.append((2, i, j)) # 加算する処理をキューの右に追加
            q.append((1, j))    # 子頂点を探索する処理をキューの右に追加
    # 処理2：親頂点に子頂点のサイズを加算
    else:
        i, j = e[1], e[2]
        # 親頂点に子頂点のサイズを加算
        memo[i] += memo[j]

# 答えを出力
for i in range(N):
    print(memo[i])

加算する処理を先にキューへ追加することで、その処理が呼ばれる時には子頂点のサイズが確定されてる状態に出来ます。
これで、スタック型DFSの問題を解決できました。

ダイクストラ法→01BFSで高速化

ARC177-Cをボクはダイクストラ法で提出しました。
制約は2.5秒なので結構ギリギリです。定数倍が少し増えるだけでTLEになりそうなラインです。

提出コード
こちらを01BFSに変更した結果こうなりました。

提出コード
まさに01BFS無双です。これが$O(1)$の威力ですね。
writerさんがPythonのダイクストラ法に忖度してくださったので何とかなりましたが、01BFSしか間に合わない制約なら解けなかったかもしれません。

コストに負を含む場合はダイクストラは使えないよ

今回の話に直接関係はありませんが、コストが出てきたら必ずダイクストラが使えるわけではありません。
コストに負を含む場合は、ベルマンフォード法を使用するらしいです。
この記事がわかりやすいと思います。
ちなみにボクはわかっていません^^
気が向いたら履修します。

01BFSのあまりにも有名な問題

高橋君のパワーが強くて物を壊しがちなのは自明です。

終わりに_final

以上で本当に終わりです。
ここまでお読みいただき、ありがとうございました。

参考

BFS, DFS

ダイクストラ

01BFS