生成文法とは
生成文法(Generative Grammar)は現在、理論言語学の支配的な思潮の一つです。ノーム·チョムスキーの「The Logical Structure of Linguistic Theory」と「Syntactic Structures」を皮切りに言語学界で最も支配的なパラダイムとして位置づけられ、その後の対立パラダイムの登場にもかかわらず、今まで内部変革を通じて科学として機能しています。
言語学の細部分科の中で唯一形式科学の要件を備えており、自然科学的に研究可能な単位としての「言語」が生成文法で定義し研究する言語です。
生成文法で扱う言語は「二つ以上の認識単位が与えられた時、二つを結合して新しい認識単位を作る」メカニズムです。生成文法の目的は、このメカニズムを研究することです。
当然のことながら、生成文法以前にも言語学は存在していました。19世紀のソシュール以後、近代的な「言語学」が確立されましたが、1950年代まで言語学で扱う「言語」は社会的習慣として定義されるだけでした。このような観点から言語学の研究課題は言語的な習慣を記録して、他の文化比較することが全てでした。
1950年代に登場したチョムスキーの生成文法は、既存の構造主義言語学の核心的仮定に対して問題を提起したという点で差別点を持ちます。チョムスキーの生成文法は多くの学者に反響を呼び、50年代から80年代にかけて構造主義から生成文法へ、また認知科学へと発展しました。
生成文法は初期の計算機科学と同じ思想的ルーツを持っていたため、多くの概念を共有します。代表的には数学的過程で形式化されたアルゴリズムが両学問が共有する概念です。その他にも1950年代チョムスキーが考案した言語機械としての初期言語機関(Language Faculty)はチューリングマシンに該当します。
このような側面から見て、生成文法は人文学よりは数学や論理学に近い形式科学です。形式科学に属する数学と論理学は演繹的方法論に従い、限られた原理を通じて多様な現象を説明します。生成文法も同様に、限られた数のメカニズムで言語表現の生成と言語多様性を説明します。
言語を扱うAIでも演繹的方法論は生成文法を意味します。現在、言語AIの主流は形態素解析器などの例外を除けば帰納的方法論に従うディープラーニングになりました。しかし、依然として計算言語学と計算機科学の基礎を支える理論であるだけに、重要だと考えて生成文法に関する記事を書きます。
この記事は大きく3つのパートに分けて生成文法を説明します。まず、基本的な生成文法として以下の2つの生成文法を扱います。
- Categorial Grammar (C-Grammar)
- Phrase-structure Grammar (PS-Grammar)
そして代表的な非変換生成文法(Non-transformational Grammar)であるLFGとHPSGをそれぞれのパートに分けて説明します。
- Lexical-Functional Grammar (LFG)
- Head-driven Phrase Structure Grammar (HPSG)
この記事で説明する理論は比較的古い理論でアップデートや参考資料が少なく、私も学んでから時間が経ったので説明が不親切かもしれません。もし詳しい説明が必要でしたら連絡お願いします。
生成文法
言語は一連の単語シーケンスです。形式言語を定義する最も基本的なタスクは、文法的に構成されたシーケンスを特性化することです。したがって、単語そのものは一般的に特別な意味や形式、範疇のない単純な表現として扱われます。人工言語と自然言語を分析するための生成的方法論は、特定の文法形式に縛られません。代わりに、生成的方法論を説明するための基本的な形式が定義されます。
- Categorial Grammar (C-Grammar)
- Phrase-structure Grammar (PS-Grammar)
- Left-Associative Grammar (LA-Grammar)
これらの基本形式主義は、それぞれのカテゴリおよび規則の形式と概念派生順序が異なります。基本形式主義の形式的基礎(formal basis)は代数的定義(algebraic definition)に従います。
生成文法の代数的定義はシステムの基本構成要素を明示的に列挙し、集合理論の概念のみを使用して構成要素と構成要素間の構造的な関係を定義します。生成文法の方法論的結果の3つの要素は次のとおりです。
- Empirical : 明示的仮説の形成(formation of explicit hypotheses)
- Mathematical : 形式的属性決定(determining the formal properties)
- Computational : パーサの宣言的明細(declarative specification of the parser)
Nativism内で自然言語に対する生成文法システムは、コミュニケーションの機能的理論なしに文法的定型性を特性化しようと試みながら高い数学的(Mathematical)複雑性を持っています。したがって、問題のシステムは自然言語を非効率的に分析すると同時に、経験的(Empirical)に過小指定されます。このような欠点を避けるために、自然言語の構文分析は次のようにする必要があります。
- 自然なコミュニケーションの構成要素として機能的に設計されなければならない。
- 低い複雑度の公式理論で数学的に定義されなければならない。
- 形式言語理論と自然言語分析の属性をモジュール化され、効率的に具現されたコンピュータプログラムで方法論的に実現される。
この3つが同時に実装される必要があります。結局、言語学者はこの条件を同時に満たす文法理論を考案しました。今後説明するC-GrammarとPS-Grammarが代表的な例です。
Categorial Grammar (C-Grammar)
最初の生成文法形式主義はCategorial Grammar(C-Grammar)です。C-Grammarの組み合わせ論は、logicのfunctor-argument構造に基づいています。functorは適切な引数を値にマッピングする関数を意味します。論理関数の構造は「Fig.1」のとおりです。
C-Grammarは日本語で「範疇文法」といいますが、この記事ではC-Grammarと用語統一します。
 |
|---|
| Fig.1 : Structure of the logical function |
C-Grammarにおけるfunctorsとargumentsの役割は、カテゴリおよび規則の定義に反映されます。まず、C-Grammarを本格的に説明するため、5つの要素について定義します:W, C, LX, R, CE
-
Wはword form surfacesの有限集合です。例えば、人工言語${a_{}}^{k}{b_{}}^{k}$で集合Wはaとbを含みます。
-
Cは次のような集合です。
- basis : u and v ∈ C
- induction : if X and Y ∈ C, then also (X / Y) and (X \ Y) ∈ C
- closure : basisとinductionに指定されたものを除き、Cには何もない。
集合Cは再帰的に定義されます。開始要素uとvがCにあるため、induction clauseによっては(u/v), (v/u), (u\v), (v\u)も同様です。これはまた、(u/v)/v), (u/v)\v), ((u/v)/u), ((u/v)\u), (u/(u/v)), (v/(u/v))などはCに属します。Cは新しい要素が以前の要素から再帰的に形成される可能性があるため無限です。
-
LXは「LX⊂(W x C)」のような有限集合です。
-
Rは次の2つの規則で構成された集合です。
- 𝛼(𝑌/𝑋) o 𝛽(𝑌) ⇒ 𝛼𝛽(𝑋)
- 𝛽(𝑌) o 𝛼(𝑌\𝑋) ⇒ 𝛽𝛼(𝑋)
-
CEはCE⊆Cである完全な表現の範疇で構成された集合です。
このような定義によって、C-Grammarの組み合わせに合う暗示的パターンはFig.2とFig.3です。
 |
|---|
| Fig.2 : Implicit pattern of 𝜶(𝒀/𝑿) 𝐨 𝜷(𝒀) ⇒ 𝜶𝜷(𝑿) |
 |
|---|
| <Fig.3 : Implicit pattern of 𝜷(𝒀) 𝐨 𝜶(𝒀\𝑿) ⇒ 𝜷𝜶(𝑿) |
C-Grammarによると、${a_{}}^{k}{b_{}}^{k}$の代数的定義は次のとおりです。
- LX = $_{def}${a(u/v), b(u), a(v/(u/v))}
- CE = $_{def}${(v)}
単語aは、次の派生木(Fig.4)でそれぞれのカテゴリ(u/v)および(v/(u/v))を持つ2つの語彙定義を持ちます。
 |
|---|
| Fig.4 : Tree of C-Grammar |
Fig.4からの派生は、単語3と4の組み合わせから始まります。この初期構成だけが単語aのカテゴリ読み取り(categorial reading)を使用します。結果はカテゴリ(v)のab表現式です。これは、入力文字列に他の単語がない場合のCE定義に沿った完全な表現です。次に、単語2は最後の組み合わせの結果と結合してカテゴリ(u/v)がある表現式aabを生成します。この結果は再び単語5と結合され、カテゴリ(v)などを含む表現式aabbを生成します。
このような方式でカテゴリー(v)の完全な表現が誘導され、各表現は任意に多くの単語aと同じ数の単語bで構成されます。したがって、有限定義(finite definition)LXおよびCEは人工言語${a_{}}^{k}{b_{}}^{k}$の無限に多くの表現を生成します。しかし構造的にC-Grammarは2つの短所があります。
- 正しい中間表現は試行錯誤を経てのみ発見できます。例えば、任意の入力で正しい初期構成ができる位置が常に正確であるとは限りません。
- C-Grammarは代替語順を代替カテゴリとしてコーディングするために高度な語彙曖昧性(lexical ambiguity)を必要とします。
結果的に言語学者でさえ与えられたC-Grammarに文字列に対するFig.4のような派生木を作るために、長い時間をかけて作業する必要があります。特に${a_{}}^{k}{b_{}}^{k}$ほど単純ではない言語では特にそうです。つまり、C-Grammarに基づく分析は、多くの可能な組み合わせをテストする必要があるため、計算上非効率的です。
また、C-Grammarはtime-linear派生を許可しません。例えば、Fig.4からの派生は単語3と4で始めなければなりません。C-Grammarのカテゴリおよび規則スキーマの特徴的な構造により、${a_{}}^{k}{b_{}}^{k}$に対して任意に長い文章を派生できる代替C-Grammarを設計することは、time-linear方式では不可能です。
C-Grammarは自然言語にも適用できます。人工言語と同様に、LXおよびCEは自然言語のトークンを使用して定義されます。
- LX = $_{def}${$W _{(e)}$∪$W _{(e \backslash t)}$}, where
$W _{(e)}$ = {Julia, Peter, Mary, Fritz, Susanne, …}
$W _{(e\backslash t)}$ = {sleeps, laughs, sings, …} - CE = $_{def}${(t)}
このLXでは、sleeps, laughs, sings,...のカテゴリ(e\t)は構文論的にだけでなく意味論的にも意味があります。(e\t)はエンティティからtruth valuesへの特性関数と解釈されます。
例えば、sleepsの特性関数は、関連真理値tが1(true)なのか0(false)なのかについて各エンティティeを確認してsleeps集合を決定します。したがって、sleepsで表示された集合は、equivalent characteristic functionが 1 にマッピングされるエンティティで構成されます。
LXとCEによって、Julia(e)とsleeps(e\t)の木はFig.5の通りです。
 |
|---|
| Fig.5 : C-Grammar Tree of Natural Language - Julia sleeps |
今まで話した内容をもとに複雑な文章を確認します。
- The small black dogs sleep
限定詞は名詞と結合し、その結果である名詞句は固有名詞のように個体を表すものとみなされます。限定詞は(e/t)/e)に分類できます。つまり、名前(e)のようなものを作るための名詞(e/t)を取るfunctorに分類することができます。反面、形容詞は名詞を取って名詞を作りますが、形容詞を(e/t)/(e/t))に分類して表現することができます。
この理論によると
- LX = $_{def}${$W _{(e)}$∪$W _{(e \backslash t)}$∪$W _{(e / t)}$∪$W _{((e/t)/(e/t))}$∪$W _{((e/t)/t)}$}, where
$W _{(e)}$ = {Julia, Peter, Mary, Fritz, Susanne, …}
$W _{(e\backslash t)}$ = {sleeps, laughs, sings, …}
$W _{(e / t)}$ = {dog, dogs, cat, cats, table, tables, …}
$W _{((e/t)/(e/t))}$ = {small, black, …}
$W _{((e/t)/t)}$ = {a, the, every, …} - CE = $_{def}${(t)}
このLXとCEを基に「The small black dogs sleep」はFig.6のような派生木で分析できます。
 |
|---|
| Fig.6 : C-Grammar Tree of Natural Language - the small black dogs sleep |
C-Grammarは、意味論的functor-argument構造と統語論的組み合わせを同時に特性化することで言語学的な意味があります。理論的には、高いレベルの意味とそれに伴う制約は、一般的に言語学で望ましいと見なされます。しかし、C-Grammarの構文と意味の側面によって同時に制約を受けても、これは部分的なだけです。その理由は、C-Grammarとそのモデル-理論的意味論が自然言語コミュニケーションでどのように機能すべきかが明確でないからです。
実際、C-Grammarの構造は問題解決の性格を持つ派生を生み出します。これらの欠点は、より複雑な文章に対するC-Grammarがカテゴリの組み合わせ制限をコーディングするために非常に高い基準の語彙曖昧性を必要とするという事実によって悪化します。これは過剰生成に苦しむ「the small black dogs sleep」のC-GrammarのLXとCEによって説明されます。例えば、文章*dog Peter(t)に対するdog(e/t) o Peter(e)の組み合わせは遮断されません。 しかも、限定詞と名詞の間の一致に対する適切な処理がないため、Fig.6は、*every dogs及び*all dog のような非文法的な組み合わせを生成する可能性があります。
Phrase-Structure Grammar (PS Grammar)
生成文法の2番目の基本形式主義は、句構造文法(Phrase-Structure Grammar)です。句構造文法は再帰理論の数学的脈絡から始まり、オートマトン理論および計算複雑度理論と密接な関連があります。句構造文法の代数的定義(Algebraic definition)は次のとおりです。
句構造文法は次の4つの要素を持っています。
- $V$は有限記号集合(finite set)
- $V_{T}$は「終端記号(terminal symbol)」というVの部分集合
- $S$は「非終端記号(Nonterminal symbol)」というVからVTを除く記号
- $P$はa -> b形式の書き換え規則集合。ここでaはV+の要素で、bはV*の要素
Fig.7はチョムスキー階層という句構造規則スキーマの制限事項を示しています。
 |
|---|
| Fig.7 : The inclusion relationship of the Chomsky hierarchy |
- タイプ-0文法(制限のない文法):タイプ0文法の左および右は、終端および非終端記号の任意シーケンスで構成されます。
-
タイプ-1文法(文脈依存文法):タイプ1文法の左および右は、終端および非終端記号の任意シーケンスで構成され、右は少なくとも左と同じくらい長い必要があります。
例:A B C -> A D E C -
タイプ-2文法(文脈自由文法):タイプ2文法の左側は正確に一つの変数で構成されます。文法の右側はV+のシーケンスで構成されます。
例:A -> BC, A -> bBCc -
タイプ-3文法(正規文法):タイプ3文法の左側は正確に1つの変数で構成されます。右側は正確に1つの終端記号と最大1つの変数で構成されます。
例:A -> b, A -> bC
文法タイプが文法0から文法3に下がるほどますます制限されるため、特定のタイプの文法は下位文法のすべての制限事項を遵守します。例えば、タイプ-3文法の規則「A->bC」はタイプ2、1、0のより少ない制限を遵守します。タイプ-2のA->bBCcはタイプ-3の制限を遵守せず、下位規則タイプ-1と0の制限を遵守します。
句構造文法に対する異なる制限により、4つのタイプの句構造文法が生成されます。タイプ-3規則のみを含む句構造文法を正規文法、タイプ-2規則を含む句構造文法を文脈自由文法、タイプ-1規則を含む句構造文法を文脈依存文法、規則に制限のない句構造文法を制限のない文法といいます。
この文法の違いは、句構造文法の生成能力の違いから始まります。この文法の違いは、句構造文法の生成能力の違いから始まります。該当文法が多くの形式言語構造を繰り返し生成できる場合、文法タイプの生成能力が高いと表現します。反面、制限的な言語だけを生成できる場合、文法タイプの生成能力が低いと言います。文法タイプが複雑になるほど、計算機科学でいう計算の複雑さも比例して増加します。
句構造文法の場合、規則制限、文法タイプ、言語クラスおよび複雑度との相関関係は次のとおりです。
 |
|---|
| Table.1 : PS-Grammar Hierarchy of Formal Languages |
多項式および幾何級数的複雑性に関する上記の考慮事項は、正規文法と文脈自由文法のみが計算的に言語説明に適しているという結論につながります。最も制限的な規則、最も低い生成容量、および最も低い計算複雑度を持つ句構造文法は、タイプ-3の正規文法です。正規文法の生成能力は単一単語の再帰反復を許容しますが、再帰対応(recursive correspondences)は許容しません。
例えば、正規言語${ab_{}}^{k}$の表現は1つのaと1つ以上のbで構成されます。${ab_{}}^{k}$(k$\geq$1)に対するA(右線形)句構造文法は次のように定義されます。
- $V$ = $_{def}${S, B, a, b}
- $V_{T}$ = $_{def}${a, b}
- $P$ = $_{def}${S -> aB, B -> bB, B -> b}
句構造文法の次の文法タイプは、文脈自由文法です。文脈自由文法の例は、以下に定義された${a_{}}^{k}{b_{}}^{3k}$です。
- $V$ = $_{def}${S, a, b}
- $V_{T}$ = $_{def}${a, b}
- $P$ = $_{def}${S -> aSbbb, a -> abbb}
文脈自由文法は、タイプ-2規則の左側が単一変数の定義で構成されるため、文脈自由と呼ばれます。句構造文法で次に大きい言語クラスは、タイプ-1規則を使用して句構造文法によって生成される文脈依存文法です。文脈依存文法は$a_{1}Aa_{2}$ -> $a_{1}ba_{2}$形式に従います。(ここでbは空のシーケンスではありません。)
句構造文法では、文脈依存文法は文脈自由文法とは対照的に解釈されます。文脈自由文法は左側に単一変数だけを許容する反面、文脈依存文法は変数を他の記号で囲むことができます。$a_{1}Aa_{2}$ -> $a_{1}ba_{2}$にあるように、タイプ-1規則は特定の文脈a1_a2に対してのみ変数Aがbで書き直すことができるため、文脈に敏感です。
タイプ-1規則の左側にある変数に対して特定の環境(文脈)を指定できる可能性は、コントロールを大きく増加させ、文脈に敏感な句構造文法の生成力を向上させます。これはakbkckに対する次の句構造文法で説明されています。
- ${a_{}}^{k}{b_{}}^{k}{c_{}}^{k}$ : $V$ = $_ {def}${$S, B, C, $$D_{1}$$,D_{2}$$, a, b, c$}
- $V_{T}$ = $_{def}${a, b, c}
- $P$ = $_{def}${S -> a S B C rule 1
S -> a b c rule 2
C B -> $D _{1}$ B rule 3a
$D _{1}$ B -> $D _{1}$ $D _{2}$ rule 3b
$D _{1}$ $D _{2}$ -> B $D _{2}$ rule 3c
B $D _{2}$ -> B C rule 3d
b B -> b b rule 4
b C -> b c rule 5
c C -> c c rule 6}
文脈に応じてシーケンス順序を変更できる可能性は、文脈自由文法よりもはるかに高いレベルのコントロールを提供します。しかし、文脈依存文法は計算複雑度が高いという欠点があります。この複雑度は大きすぎるため、状況に応じた構文文法クラスの実用的な構文分析アルゴリズムが存在しません。つまり、文脈依存文法は計算が難しいのです。自然言語に対する句構造文法の簡単な適用は、次の定義で説明されています。比較を容易にするため、C-GrammarのFig.6と同じ文章を例に挙げます。
- $V$ = $_{def}${S, NP, VP, V, N, DET, ADJ, black, dogs, little, sleep, the}
- $V_{T}$ = $_{def}${black, dogs, little, sleep, the}
- $P$ = $_{def}${S -> NP VP,
VP -> V,
NP -> DET N,
N -> ADJ N,
N -> dogs,
ADJ -> little,
ADJ -> black,
DET -> the,
V -> sleep}
この形の句構造文法は文脈自由文法です。規則の左側は1つの変数だけで構成されているため文脈依存文法ではなく、一部規則の右側には2つ以上の変数が含まれているため、正規文法でもありません。
Fig.6のC-Grammar派生木と同様に、句構造文法の派生木はFig.8で表現できます。
 |
|---|
| Fig.8 : PS-Grammar Tree of Natural Language - the small black dogs sleep |
このような木構造を句構造文法では句構造(phrase structures)といいます。句構造木のカテゴリ記号をノード(node)といいます。ノード間には支配(dominance)と順位(precedence)という2つの形式的関係があります。例えば、ノードSはS -> NP VP規則に従ってノードNPおよびVPを支配します。同時に、この規則は優先順位を指定します。つまり、NPノードはVPノード左側の木に位置します。
言語の組み合わせを単語形態の複雑なカテゴリでコーディングし、構成に対して2つの規則スキーマだけを使用するC-Grammarと比較すると、句構造文法は組み合わせで表現される基本カテゴリのみを使用します。
要約すると、C-Grammarと句構造文法の形式的な違い、すなわちそれぞれの自然言語分析は異なる経験的目標によって言語的に意味が付与されます。C-Grammarの目標は自然言語のfunctor-argument構造を特性化することであり、句構造文法は自然言語の構成素構(Constituent Structure)を表現することを目的としています。
句構造文法の構成構造を扱う代表的な電算言語学方法としては、LFG(Lexical-Functional Grammar)とHPSG(Head-driven Phrase Structure Grammar)があります。まずLFGを説明します。
Lexical-Functional Grammar (LFG)
LFGは変換規則が必要ないsurface-centered構文理論です。文章内で構文的に重要な様々な関係は、形式的に異なる2つの構造を通じてLFGと表現されます。そのうちの一つが、文章内の線形関係(linear relation)と構成関係(constitutive relation)を記述する構成構造(Constituent Structure)です。
他の一つは機能構造(Functional Structure)で、主語、目的語、修飾語、意味主語(semantic subject)などConstituent Structure(C-Structure)に該当する文法的機能に関する情報が含めています。
ここからConstituent StructureはC-Structure、Functional StructureはF-Structureと用語統一します。
まとめると、LFGの理論的特徴は、意味論的重要性を持つ述語論証構造に関する情報を含んでいるF-Structureと表層のC-Structureの間の対応関係を記述できることです。
LFGで許容される句構造規則は、規則の右側に現れる非終端記号が選択的に文法機能と関連した追加情報を含めることができます。Fig.9がLFGでのC-Structureの例です。
 |
|---|
| Fig.9 : Constituent Structure of LFG |
Fig9.aの右側に表示された非終端記号NPの下には主語に関する情報が追加され、この追加情報を含む方程式をfunctional schemaといいます。functional schemaで矢印は変数です。「↑」は矢印が配置されたコンポーネントをすぐに支配するノードによってインスタンス化され、「↓」はそのノード自体によってインスタンス化されます。
したがって、Fig.9.a.のNPの下に追加されたfunctional schemaは、「↓」で表示されたNP自体が「↑」で表示されたSの対象になることを意味します。同様に、Fig9.b.でVのすぐ後ろにNPの下に追加されたfunctional schemaは、NPがVPの直接目的語として機能することを意味します。
LFGにはメタ変数がさらに2つ設定されます。「⇑」変数は制御役割(controller)をするコンポーネントの機能構造を、「⇓」変数は被制御役割(controllee)をするコンポーネントの機能構造を意味します。このメタ変数はFig.10で見られます。
 |
|---|
| Fig.10 : Constituent Structure of controller and controllee |
上記の規則は、名詞句とこの名詞句が除外される文章の組み合わせを許可する句構造規則です。この規則でコンポーネントNPの下に添付された機能ダイヤグラム「↓=⇓」は、この名詞句が被制御役割(controllee)をするコンポーネントを意味します。そして、この被制御単語(controllee)に対する制御単語(controller)は、次に出てくるコンポーネントSにあります。それでは簡単な英語LFG文法を説明します。
 |
|---|
| Fig.11 : E-LFG |
F-Structureを生成する過程でfeature structureの統合(unification)に関与する統合アルゴリズム(unification algorithm)が作動し、統合アルゴリズムは次のように定義されます。
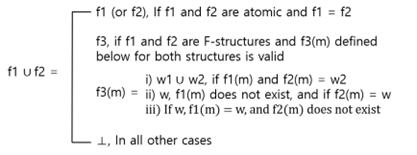
Fig.11の句構造規則を使用してFig.12 のようなfunctional schemaを持つC-Structureを得ます。
 |
|---|
| Fig.12 : C-structure with functional schema attached |
functional schemaがあるC-Structureは、構文論的に純粋なC-Structureと意味論的なF-Structureの間に位置する構造として理解できます。次はfunctional index fnを上から下に、左から右に非終端ノード数だけ割り当てます。Fig.13は、functional indicatorが割り当てられたC-Structureを示しています。
fnからnは任意の数字を意味します。
 |
|---|
| Fig.13 : Fig.12 with fn |
function indexが付いているFig.13の各メタ変数を該当function indexに交換するとFig.14のような木構造ダイアグラムが生成されます。
 |
|---|
| Fig.14 : Fig.12 with functional equations |
このようなfunctional equationは上から下に、左から右に抽出されます。それでは、functional equationは次のようになります。
- (f1 SUBJ) = f2
- F1 = f3
- F2 = f4
- (f2 PRED) = ‘Peter’
- (f2 PERS) = 3
- (f2 NUM) = sg
- F3 = f5
- (f3 PERD) = ‘love<(↑ SUBJ)(↑ OBJ)>’
- (f3 TENSE) = present
- (f3 SUBJ PERS) = 3
- (f3 SUBJ NUM) = sg
- (f3 OBJ) = f6
- f6 = f7
- (f6 PRED) = ‘Mary’
- (f6 PERS) = 3
- (f6 NUM) = sg
次のステップは、functional equationを利用して文章のF-Structureを作る過程で、これを一つずつ追加するとFig.15のような最後のF-Structureが作られます。
 |
|---|
| Fig.15 : Final Version of F-Structure |
Head-driven Phrase Structure Grammar (HPSG)
HPSGは依存文法(dependency grammar)とは異なる句構造文法の理論であり、一般化された句構造文法の発展した文法規則です。HPSGはLFGと同様に、統合アルゴリズムに従って各単語と統合性に関する情報を入れて句構造規則を生成します。
HPSG文法には、一般的に文法に属するとはみなされない原則と文法規則、語彙項目が含まれます。HPSGが扱う基本タイプは記号(sign)です。単語と句(phrase)は記号の2つの下位タイプです。単語には以下の2つの機能があります。
- [PHON] : 音、音声形式
- [SYNSEM] : 統語的(syntactic)及び意味論的(semantic)情報
記号と規則は、形式化された機能構造で公式化されます。HPSGは、type hierarchy内での位置と属性値行列(Attribute Value Matrix)で表される内部機能構造で定義される記号を結合して文字列を生成します。
Featureは、typeまたはFeatureリストを値として使用し、これらの値は固有のFeature構造を持つことができます。文法規則は主にお互いに対する制約記号(constraints signs)を通じて表現されます。記号のFeature構造は、記号の音韻論的、統語論的、意味論的属性を説明します。
一般的な表記法では、機能は大文字で、featureはイタリック体の小文字で作成されます。AVMの番号が付けられたインデックスは、トークンと同じ値を意味します。
以下の動詞「walks」に対する単純化されたAVMにおいて、動詞のカテゴリ型情報(Categorical Information)はこれを説明する機能(HEAD)とそのargumentを説明する機能(VALENCE)に分けられます。
 |
|---|
| Fig.16 : HPSG AVM for the verb “walks” |
「walks」はtype動詞のheadであるtype単語の記号です。自動詞の「walks」には補語がありませんが、三人称単数名詞の主語が必要です。主語(CONT)の意味値は、動詞の唯一のargumentとともに索引されます。「she」に対する次のAVMは、要求事項を満たすことができるSYNSEM値がある記号を示します。
 |
|---|
| Fig.17 : HPSG AVM for the word “she” |
type phraseの記号は1つ以上のchildrenと統合され、情報を上に伝えます。次のAVMは、head-subj-phraseに対する支配規則をエンコードします。ここには二つのchildren、head children(動詞)と動詞のSUBJ制約条件を満たすheadではなくchildrenが必要です。
 |
|---|
| Fig.18 : HPSG AVM of a head-subj-phrase |
最終結果は動詞head、空いてる下位分類機能および2つのchildrenを持つ音韻的な情報が含まれた記号になります。
 |
|---|
| Fig.19 : HPSG tree of a head-subj-phrase |
最後に
最後まで読んでいただき、ありがとうございました。この記事では、計算言語学の基本理論となる生成文法について取り上げました。最近はほとんど見当たりませんが、それなりの意義がある学問だと思います。
今は生成文法で計算言語学を研究しているところがあるかどうかは分かりませんが、もし計算言語学を研究している方がいらっしゃったら是非ご連絡ください。