最近DIGITSでAlexNetやGoogLeNetで
画像認識タスクをやらせています。
Qiitaでの数式記述方法の練習を兼ねて
ニューラルネットワーク(NN)の構成要素を数式表現で復習していきます。
ディープラーニングと呼ばれるNNを簡潔に記述できれば
備忘録になりますので便利です。
畳み込み層
活性化関数
1.シグモイド関数
多層パーセプトロンの説明はこれが多い
f(u)=\frac{1}{1+e^{-u}}
多層パーセプトロンの重み付き結合
u=\sum^n_{i=1}w_ix_i
2.tanh関数
Relu関数の方が精度が高いとわかるまでこっちが主流だったそうです
tanh(u)=\frac{exp(u)-exp(-u)}{exp(u)+exp(-u)}
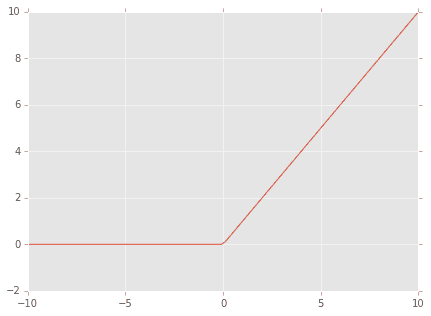
3.ReLU関数(Rectified Linear Unit)
サンプルでディープラーニングを実行すると畳み込みの計算は大抵これ
f(x)=max(0,x)
出力層
誤差関数
交差エントロピー(cross entropy)関数
このページトップのDIGITSで実行した様な
多クラス分類の場合にlossの計算に使用する
yは教師信号 rは出力信号
Cは分類クラスの個数
Nは出力層のニューロンの個数
E=-\sum_{c=1}^C\sum_{n=1}^Nr_{cn}ln(y_{cn})
2クラス問題の場合
E=-\sum_{n=1}^Nr_nlny_n+(1-r_n)ln(1-y_n)
二乗誤差関数
最小二乗法でお馴染みの誤差関数
回帰問題を解かせる時に使用
E=\sum_{n=1}^N {||r_n-y_n||}^2
尤度関数
ソフトマックス関数
出力層で畳み込み層もしくはプーリング層から
出力された情報から確率 Φを出力する
\phi(v_i)=\frac{e^{v_i}}{\sum_i e^{v_i}}
ネットワークの学習方法
確率的勾配降下法
学習則にはいくつか種類がある
バッチ学習
すべての学習サンプルに対して誤差を求めてから
ネットワークの結合重みを更新する方法
時間はかかるがノイズを抑える
ここでEは誤差関数であり上述の
交差エントロピー(cross entropy)関数または二乗誤差関数を用いる
繰り返し回数t回目の各学習サンプルに対する誤差をE^t_nとする
すべてのサンプルに対する誤差E^tを下記のように求める
wは結合重み(weight)
ηは学習係数という、
重み更新時の誤差を大きく修正するなら値を大きくし
小刻みに修正する場合は小さい値を入れるとよし
(DIGITSの場合はStepDownで自動修正されたりする)
E^t=\sum^n_{n=1} E^t_n
w^{t+1}=w^t-\frac{\partial E^t_n}{\partial w^t}
逐次学習
学習サンプル一枚ずつに対して更新する方法
早いけどノイズを学習する
変動が大きい為、学習が収束しない可能性あり
ミニバッチ学習
逐次学習のバッチ学習の中間
普通に考えれば性能試験に便利なのでこの方法がとられると思う
Dは学習サンプルを小切りにしたサブセット
サブセット毎に誤差を出してから更新する。
E^t=\sum_{n∈D}E^t_n
勉強していきながら数式を確認する為に
内容は逐次追加しています。