電子工作にモデルベース開発(Model Based Development: MBD)を適用してみた【プラントモデル編】

はじめに

この記事は、下記の続き物です。

電子工作にモデルベース開発(Model Based Development: MBD)を適用してみた【コントローラモデル編】

上記の記事では、モデルベース開発(以下MBD)の何たるかと、そのうま味について、コントローラーモデルを作って解説をしました。
今回の記事は、MBDのもうひとつのモデルであるプラントモデルについて、実際にプラレールの車両モデルを構築して、MBDのうま味(とくにプラントモデルにフォーカスした内容)について解説していきたいと思います。
というわけで、この記事は上記記事のつづきものになりますので「MBD is 何？」という人や、今回の電子工作の題材(プラレール魔改造)について知りたい人は、上記の記事をご覧いただいてから以下をお読みいただければと思います。

今回やること

• 「プラレール車両プラントモデル(1Dマルチドメイン非因果系モデル)」を構築する
• 前回作った「スピードコントロールモデル(コントローラモデル)」と合体して、連成シミュレーション(Co-Simulation)する

プラントモデルについて

これからさっそくプラントモデルを構築するのですが、その前にプラントモデルに関するあれやこれやを整理しておきたいと思います。

プラントモデルの心得

プラントモデルを作るときに忘れがちなコトを、自戒の念を込めてまずは書き記したいと思います。

【心得その1】 目的はあくまで「モノを作ること(コントローラモデルのロジックを作ること)」と肝に銘じるべし。

プラントモデル構築あるあるなのですが、このプラントモデルというヤツは、これはこれで作り込んでいってシミュレーションをしていくうちに、だんだん現実世界と挙動が合ってきて楽しくなってきます。そうするとふとした瞬間、目的と手段がすり替わっている自分自身に気が付きます。いつの間にかモノを作ることを忘れて、プラントモデルを作ることが目的になってしまってるんですね。
コントローラモデルと違い、プラントモデルはモノを直接作ることに作用しません。プラントモデルに時間をかければ精度は良くなりますが、いくら時間をかけてもモノは出来上がらないことは頭の片隅に入れておきましょう。¹

【心得その2】 ロジックのドコを検証したいかを明確にして、モデルのリダクションを心がけるべし。

プラントモデルの汎用性・再利用性を考えていくと、どうしても対象のモノの全ての現象を再現するようなモデルを作りたくなってしまうんですが、残念ながらモノの挙動を全部てんこ盛りにしたモデルを作ると、軽々と「シミュレーション時間 >>> 実時間」になります。例えば「10sec間の挙動をシミュレーションをするのに、計算時間がウン日かかる」みたいなハナシです²。なので、「ロジックのドコを検証したいのか？」を忘れずに、その部分にフォーカスした、スマートなモデル作りを心がけましょう。
プラレール車両モデルに、走行中の空力まで考慮したナビエ・ストークス方程式を盛り込んだらそりゃやりすぎだわ！...って今は思うじゃん？作っていくと、結構その沼にハマるんですよ・・・。

プラントモデルの分け方

プラントモデルの分類には、特徴に応じて下記のような分け方があります。

【分け方その1】 0D / 1D / 3D

モデルの表現するディメンジョン...というより、どちらかというと「数値解析処理の複雑さ」で分けている節があります。特に「0D / 1D」が何を指すかは人によって揺らぎがあります。ワタシの業界(自動車エンジン開発)の雰囲気だと、

• 3D
  空間偏微分要素(∂x, ∂y, ∂z)を使った、分布的解析(流体系・燃焼系・応力などの構造系)モデル
• 1D
  時間微分要素(dt)をつなぎ合わせて、機械・電気・熱などのエネルギー授受関係を表すモデル
• 0D
  エンジンの燃焼や触媒浄化化学反応などの、複雑で方程式として表すことが困難なものに対して、統計モデル(マップ)で表すもの

と、言ってる人が多いように感じます。(ウチの業界ではこう分けてるよ！という方はコメントお待ちしております)

【分け方その2】 非因果系 / 因果系

これは特に1D(0D)シミュレーション特有の分け方になりますが、モデルの構築手法に「因果系モデリング」と「非因果系モデリング」という考え方があります。

• 因果系モデル
  数式の変数(=信号)の入出力を明確にしてモデリングする方法。方程式はモデルを作る人が数式を整理してモデリングしないといけない。
• 非因果系モデル
  方程式のままモデリングする方法。「バネ-マス-ダンパ」「抵抗-コイル-コンデンサ」という部品単位でブロック構築できる。(ブロック接続した後に、ツールが方程式を解析してくれる)

ざっくりした説明は以上なのですが、ちゃんと知りたい方はコチラにとっても詳しく書かれていますのでご覧ください。

【分け方その3】 分野特化型 / マルチドメイン

たとえば...
「Nastran ... 構造解析シミュレーション」「SPICE ... 電気回路シミュレーション」「ANSYSのCFD ... 熱流体解析シミュレーション」
...など、以前はシミュレーションと言えば、分野特化型が主流でした。³
ところが、MBDにおいては“マイコンの指示値が、制御対象にどのような挙動を与えるか？”が最大の関心事であり、その対象(プラント)とは「物理分野を跨いだオーバーオールの挙動」として知りたいことがほとんどです。
オーバーオールの挙動の表し方の一つとして、制御工学をやられている方たちにはおなじみの「伝達関数」表現や「状態空間」表現があったりするのですが、あそこまでの抽象度ほどではなく、「運動(回転・直線)」「電磁気」「熱・流体」などの分野(ドメイン)を一緒くたにモデリングする手法が マルチドメイン と呼ばれる手法です。

以上、3つの切り口でプラントモデルの分類の仕方について書いてみましたが、ここで昨今のMBD業界の流行りとして、MBDにおけるプラントモデル(物理モデリング)は、 「1D(0D)・マルチドメイン・非因果系モデリング」 で構築するケースが多いです。今回のプラレール車両モデルも、流行りに乗っかって「1D・マルチドメイン・非因果系モデル」で作ってみようと思います。というわけで、ここより先「プラントモデル」とは「1D・マルチドメイン・非因果系モデル」を指すこととします。⁴

モデル構築ツールについて

コントローラモデル構築ツールの時は「MATLAB/Simulink」の事実上一択と述べましたが、プラントモデルの構築ツールは各社からいろんなツールがでています。⁵
今回は、代表的な非因果系モデリング記述言語であるModelica系の中から、無料で使えるOpenModelicaというツールを利用してプラレール車両モデルを作ってみたいと思います。
そして、最終的には前回構築したコントローラモデルとくっつけてシミュレーションしたいので、OpenModelicaで作ったプラントモデルをFMU(Function Mockup Unit)という形式で書き出してSimulinkに取り込み、連成シミュレーション(Co-Simulation) をしてみたいと思います。
なので、使うツールは「OpenModelica」と「MATLAB/Simulink」の合わせ技です。
「んな、まどろっこしいやり方しなくても、Simulinkでプラントモデル作ればいいんじゃないの？」と疑問を持たれる方がいるかもしれませんが、Simulinkで作れるプラントモデルは因果系モデルであり、非因果系モデルは作れません。⁶
この記事では後ほど「非因果系モデリング」のうま味についても触れたいと思います。

プラレール車両モデルの概要

さて、それでは早速プラントモデルの構築をしてみたいと思います。
実はこのプラントモデルを作るより前にプラレールを魔改造して実機を作ってしまったのですが、そこで実際に起きた出来事として、プログラムを走らせたときにギヤのフリクションがすごくて、なかなか弱電圧をかけても動き出さないという事象に出くわしました。ですので、今回はこれをケーススタディとして「発進時の静止摩擦に打ち勝つための電圧補正(コントローラモデル)を検討したい」という目的の下、「どんな電圧をかけたら、プラレールは動きだすのか？」に焦点を当てたプラントモデルを構築したいと思います。

プラレール車両モデルに考慮すべき要素としては、こんなかんじでしょうか。

• コントローラ(マイコン)からモーター印加電圧を受け取る
• DCモーターが回ってトルク(回転運動)に変換
• 回転運動は「ギヤ」を介して車輪に伝達
  • ギヤは「減速」するほか、「フリクション」と「イナーシャ(回転慣性モーメント)」がある
• 車輪が回ってプラレールが走る(直線運動に変換)
  • プラレールには「車両重量」と「レールとのフリクション」がある

この絵をベースに、OpenModelicaでモデル構築していきます。

モデルの作成

OpenModelicaに限らず、ちまたの1Dマルチドメインシミュレーションツールは各物理ドメインごとに「部品(ブロック)」が予め定義されており、それらを持ってくるだけでモデルが出来上がってしまいます。

今回のプラレール車両モデルも、標準部品だけで出来上がりました！
非因果系モデリングとは、物理要素をつなぐだけでそれら要素間の振る舞い(微分代数方程式)を自動的にツール側が解析してくれます。このため、因果系モデリングでよくハマる「代数ループ」などの罠を意識することなく、直感的にモデル構築ができるのがメリットです。
もう少し具体的な説明をしてみます。さっきのポンチ絵の時には書いた「車両とレール間のフリクション」という要素ですが、モデルでは省きました。省くのが適か否かという問題はさておき、因果系モデリングでは「省くor省かない」かで、モデルの内部を大幅に修正する必要があります。それに対し、非因果系モデリングでは該当部分に「フリクション要素」を後ろに足すだけで済むんです。数学的なテクニックを切り離し、使う側は物理要素のみを意識すればモデル構築が容易にできること。これが非因果系モデリングのうま味になります。⁷

パラメータの設定

ブロック配置したら、つぎは各ブロックのパラメータの設定をしていきます。
本当だったら、ちゃんと測定とか計算をしてパラメータを決めていきますが、今回は構築時点で残念ながら現物(プラレール本体)が手元になかったため、完全な妄想でパラメーター設定してしまいました。
以下に、今回構築した「プラレール車両モデル(妄想設定値込み)」を貼り付けておきます。「モーター印加電圧」には、「ランプ信号ブロック」を入れておきましたので、OpenModelicaなどのModelica系ツールがあれば、そのまま動くはずです。

プラレール車両モデル(妄想設定値込み)

PlaRail.mo

model PlaRail
  Modelica.Electrical.Machines.BasicMachines.DCMachines.DC_PermanentMagnet dc_motor(IaNominal = 0.66, Jr(start = 2.5e-6), TaNominal = 298.15, VaNominal = 1.5, wNominal = 731.991) annotation(
    Placement(visible = true, transformation(origin = {-60, 20}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
  Modelica.Electrical.Analog.Sources.SignalVoltage signalVoltage annotation(
    Placement(visible = true, transformation(origin = {-60, 46}, extent = {{10, -10}, {-10, 10}}, rotation = 0)));
  Modelica.Electrical.Analog.Basic.Ground ground annotation(
    Placement(visible = true, transformation(origin = {-92, 46}, extent = {{-10, -10}, {10, 10}}, rotation = -90)));
  Modelica.Mechanics.Rotational.Components.Inertia inertia(J = 5.0e-5) annotation(
    Placement(visible = true, transformation(origin = {-30, 20}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
  Modelica.Mechanics.Rotational.Components.BearingFriction friction(peak = 1.5, tau_pos = [0, 0.04; 10, 0.012; 15, 0.008; 20, 0.0065; 25, 0.0052; 30, 0.0062; 35, 0.0072; 40, 0.0082; 45, 0.0092; 50, 0.0102; 55, 0.0112; 60, 0.0122; 65, 0.0132], useSupport = false, w_small = 1.0e-5) annotation(
    Placement(visible = true, transformation(origin = {-2, 20}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
  Modelica.Mechanics.Rotational.Components.IdealGear reductionGear(ratio = 20.0) annotation(
    Placement(visible = true, transformation(origin = {28, 20}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
  Modelica.Blocks.Math.UnitConversions.To_rpm to_rpm annotation(
    Placement(visible = true, transformation(origin = {84, 48}, extent = {{-8, -8}, {8, 8}}, rotation = 0)));
  Modelica.Mechanics.Rotational.Sensors.SpeedSensor sen_RevSpd annotation(
    Placement(visible = true, transformation(origin = {56, 48}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
  Modelica.Mechanics.Rotational.Components.IdealRollingWheel wheel(radius = 2e-2) annotation(
    Placement(visible = true, transformation(origin = {-4, -20}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
  Modelica.Mechanics.Translational.Sensors.SpeedSensor sen_CarSpd annotation(
    Placement(visible = true, transformation(origin = {32, -42}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
  Modelica.Mechanics.Translational.Sensors.ForceSensor sen_CarForce annotation(
    Placement(visible = true, transformation(origin = {32, -20}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
  Modelica.Mechanics.Translational.Components.Mass carMass(m = 200e-3) annotation(
    Placement(visible = true, transformation(origin = {64, -20}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
  Modelica.Blocks.Sources.Ramp ramp(duration = 3, height = 5)  annotation(
    Placement(visible = true, transformation(origin = {-88, 82}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
equation
  connect(ground.p, signalVoltage.n) annotation(
    Line(points = {{-82, 46}, {-70, 46}}, color = {0, 0, 255}));
  connect(signalVoltage.n, dc_motor.pin_an) annotation(
    Line(points = {{-70, 46}, {-70, 30}, {-66, 30}}, color = {0, 0, 255}));
  connect(signalVoltage.p, dc_motor.pin_ap) annotation(
    Line(points = {{-50, 46}, {-50, 30}, {-54, 30}}, color = {0, 0, 255}));
  connect(dc_motor.flange, inertia.flange_a) annotation(
    Line(points = {{-50, 20}, {-40, 20}}));
  connect(inertia.flange_b, friction.flange_a) annotation(
    Line(points = {{-20, 20}, {-12, 20}}));
  connect(friction.flange_b, reductionGear.flange_a) annotation(
    Line(points = {{8, 20}, {18, 20}}));
  connect(sen_RevSpd.w, to_rpm.u) annotation(
    Line(points = {{67, 48}, {74, 48}}, color = {0, 0, 127}));
  connect(reductionGear.flange_b, sen_RevSpd.flange) annotation(
    Line(points = {{38, 20}, {43, 20}, {43, 48}, {46, 48}}));
  connect(reductionGear.flange_b, wheel.flangeR) annotation(
    Line(points = {{38, 20}, {43, 20}, {43, 0}, {-24.5, 0}, {-24.5, -20}, {-14, -20}}));
  connect(wheel.flangeT, sen_CarForce.flange_a) annotation(
    Line(points = {{6, -20}, {22, -20}}, color = {0, 127, 0}));
  connect(sen_CarForce.flange_b, carMass.flange_a) annotation(
    Line(points = {{42, -20}, {54, -20}}, color = {0, 127, 0}));
  connect(wheel.flangeT, sen_CarSpd.flange) annotation(
    Line(points = {{6, -20}, {22, -20}, {22, -42}, {22, -42}}, color = {0, 127, 0}));
  connect(ramp.y, signalVoltage.v) annotation(
    Line(points = {{-76, 82}, {-60, 82}, {-60, 58}, {-60, 58}}, color = {0, 0, 127}));
  annotation(
    uses(Modelica(version = "3.2.3")),
    Diagram(graphics = {Text(origin = {70, 89}, extent = {{-26, 7}, {26, -7}}, textString = "プラレールモデル", fontName = "Meiryo UI"), Rectangle(origin = {-73, 42}, lineColor = {127, 183, 255}, fillColor = {255, 255, 255}, fillPattern = FillPattern.Backward, borderPattern = BorderPattern.Raised, extent = {{31, 20}, {-27, -18}}, radius = 5), Rectangle(origin = {-45, 16}, lineColor = {135, 230, 114}, fillColor = {255, 255, 255}, fillPattern = FillPattern.Backward, borderPattern = BorderPattern.Raised, extent = {{97, 20}, {-7, -12}}, radius = 5), Rectangle(origin = {-11, -24}, lineColor = {234, 127, 255}, fillColor = {255, 255, 255}, fillPattern = FillPattern.Backward, borderPattern = BorderPattern.Raised, extent = {{97, 20}, {-7, -28}}, radius = 5), Text(origin = {-47, 64}, lineColor = {99, 147, 200}, extent = {{-7, 4}, {7, -4}}, textString = "電気系", fontSize = 20, fontName = "Meiryo UI"), Text(origin = {75, 0}, lineColor = {183, 99, 200}, extent = {{-7, 4}, {7, -4}}, textString = "直線運動系", fontSize = 20, fontName = "Meiryo UI"), Text(origin = {-13, 40}, lineColor = {99, 200, 133}, extent = {{-7, 4}, {7, -4}}, textString = "回転系", fontSize = 20, fontName = "Meiryo UI")}, coordinateSystem(initialScale = 0.1)));
end PlaRail;

シミュレーション&デバッグ

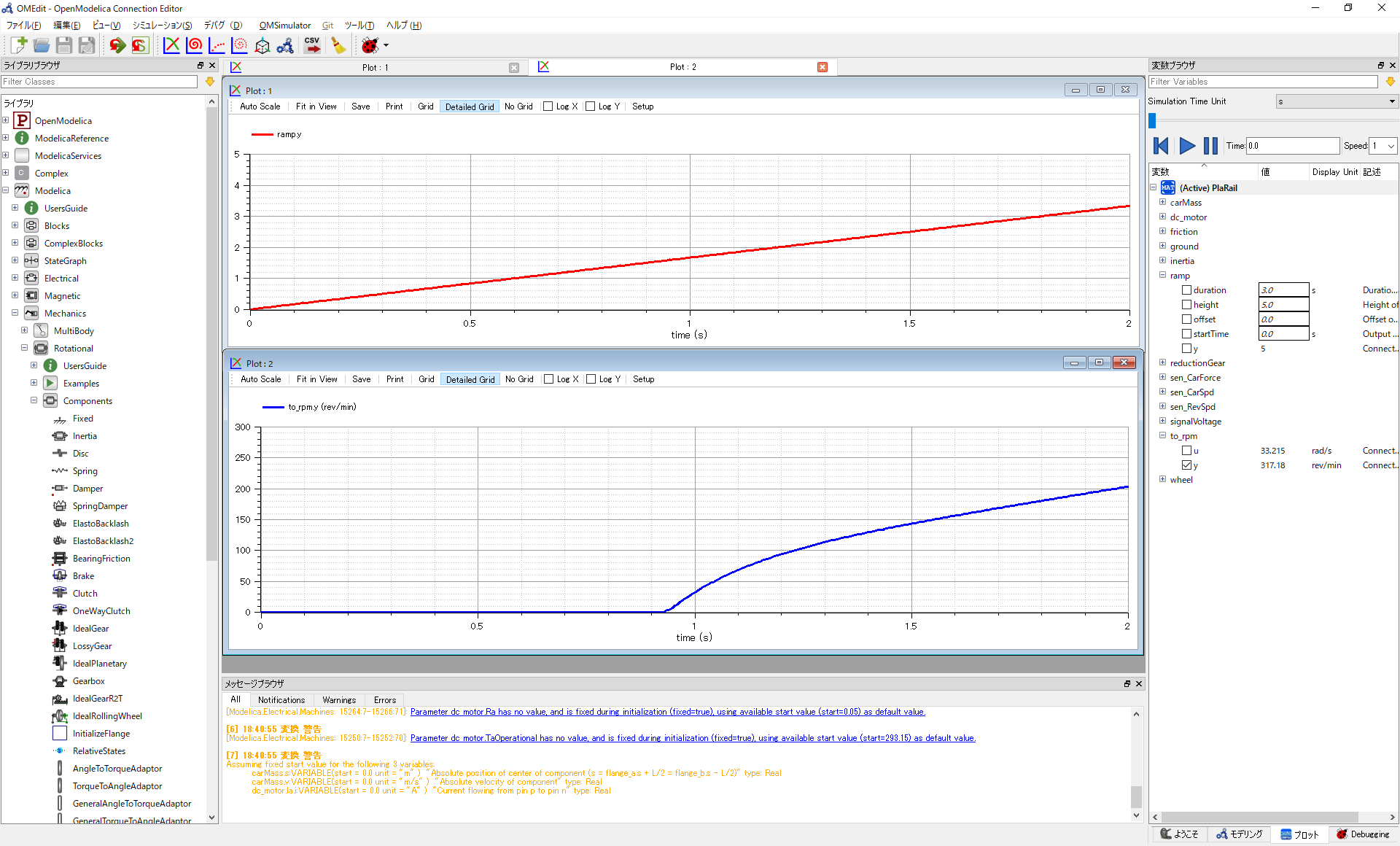
パラメータ設定したら、それっぽい挙動かどうかを確認するため、OpenModelica上でシミュレーションします。
発進をイメージして、モーター印加電圧にランプ信号を入れてみた結果です。

徐々に電圧を印加していくと(赤線)、最初は動かないけど、あるところから突然動き出す(青線)という挙動になりました！これは、実機と同じ挙動です！
もし、実機と同じ挙動にならない場合は、

1. 実機では起こっている“何かしらの物理現象”を要素(ブロック)に落とし込めていない
2. 要素(ブロック)内のパラメーターが実機と合っていない

このいずれかの可能性が高いので、実機の挙動を再現するようにパラメーターの調整をしていきます。
さぁ、どんどん調整をして実機挙動を完全再現——・・・あ、心得を忘れないように！(忘れてるところだった・・・)

FMUエクスポートとインポート

プラントモデルの構築が終わったら、次はコントローラモデルとつなげる準備を行います。
異なるツールで作ったプラントモデル間や、コントローラモデルとの間をつないで、連携させながらシミュレーションすることを連成シミュレーション(Co-Simulation)といいます。そして、ツールの分け隔てなくつなぐ仕組みにFMI(Functional Mockup Interface)という規格があります。
FMIの規格に沿って書き出したモデルはFMU(Functional Mockup Unit)と呼ばれ、規格に対応したツールならFMUをインポート/エクスポートできます。

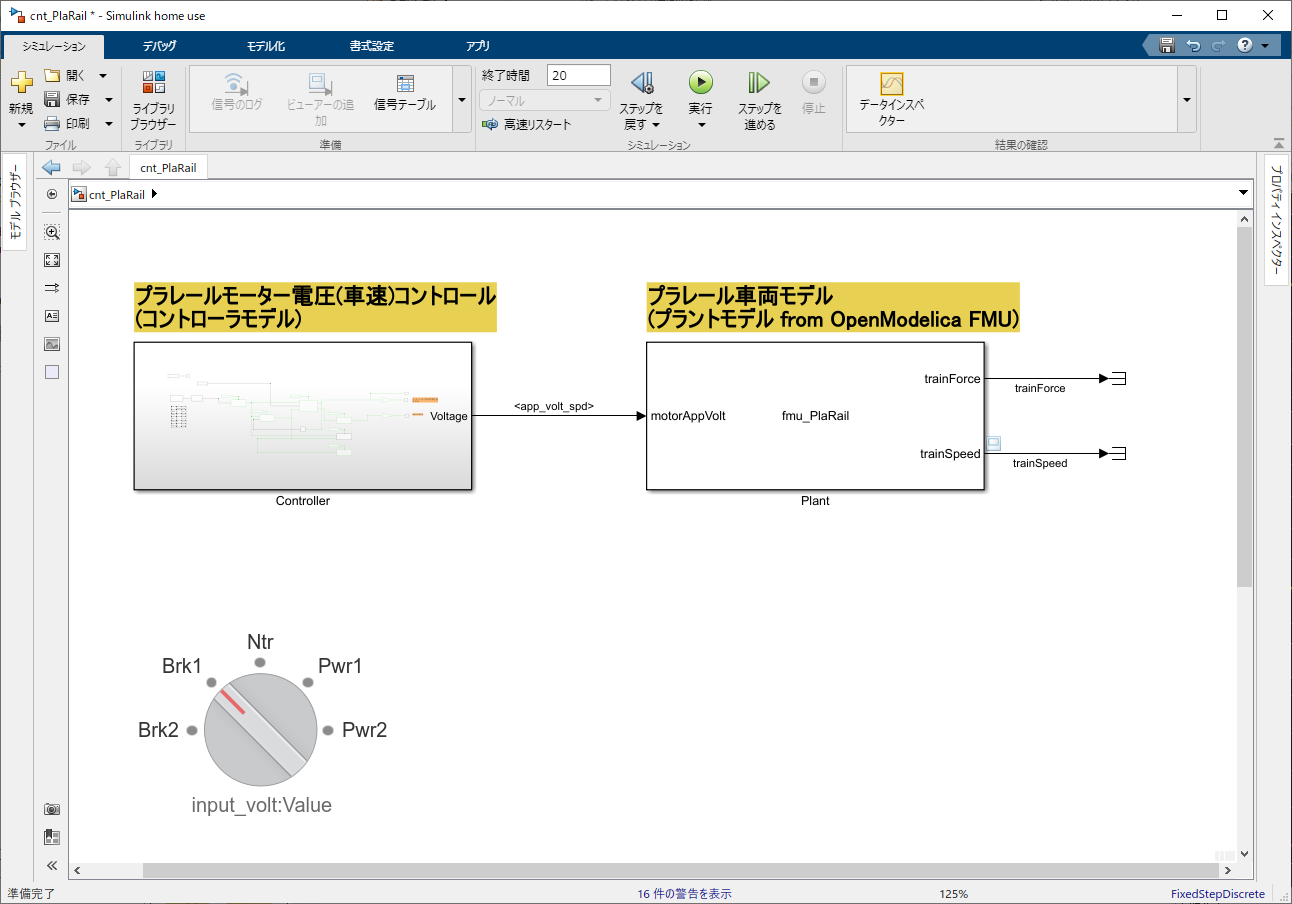
今回は、OpenModelicaで作ったプラントモデル(プラレール車両モデル)をFMUエクスポートしてSimulinkに取り込み、Simulinkで作ったコントローラモデル(プラレールスピートコントロールモデル)とつなげます。
OpenModelicaのFMUエクスポートは簡単で、File -> Export -> FMUでエクスポートできます。⁸

こうしてできたFMUモデルを今度はSimulinkに取り込むのですが、これも簡単で、Simulinkモデル上にFMUブロックを置き、さっきエクスポートしたFMUファイルを指定してあげれば、取り込み完了です！

あとは、コントローラモデルとプラントモデルをつなげば、Co-Simができます！マスコンからの加減速モード指示で車両が動きます！(プラントモデルのTrain_Speedが上がる)

Co-Simulation

それでは早速シミュレーションして、発進補正について検討してみましょう。

まずは、発進補正がない場合のシミュレーション結果です。
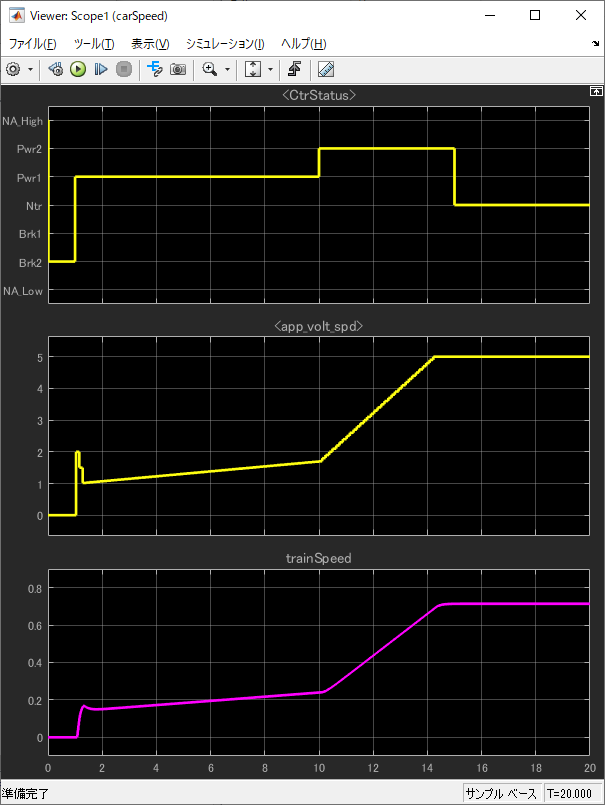
グラフは上段: マスコン指示、中段: モーター印加電圧、下段: 車両速度(プラントモデル)です。

1secの発進指示で、最初1Vのオフセット電圧かさ上げをしていますが、プラレールは動き出しません。こんな程度のオフセット電圧ごときでは静止摩擦に勝てないようです。
しばらくすると、静止摩擦に打ち勝つトルクをモーターが出せるため、プラレールは(突然)動き出しますが、これでは 加速してほしいときに動いてくれない なんだかもどかしいプラレールになってしまいます。では、どのようにロジックを修正すれば良いでしょう？

というわけで、ロジックに“発進補正”を入れて修正してみました。

“発進補正”として、インパルス的な電圧を入れることで、静止摩擦に打ち勝つトルクを与えました。これにより、加速してほしいときに動くプラレールにすることが 実機無しで検証することができました！

MBD(プラントモデル)のうま味とは？

発進補正を入れれば、ちゃんと加速してほしいときに動くプラレールを作れることが、実機なしで(プラントモデルによって)確認できましたが、例えば「どのぐらいの電圧補正値にすれば動き出すか？」などの値を詰める作業は(いわゆる「チューニング」)、プラントモデルの精度を相当高めないといけません。そうすると、プラントモデルを作り込むよりも実機作っちゃって評価した方が早くね？という現象に陥ったりもして、「結局MBD(プラントモデル)って、どういうタイミングで使えばいいの？」なんていう疑問が出てきます。
この疑問は実はとても難しく、一律に答えを出すことはできないのですが、ここではうま味を引き出す考え方のヒントを提示します。キーポイントは「リソースとクオリティのバランス」です。

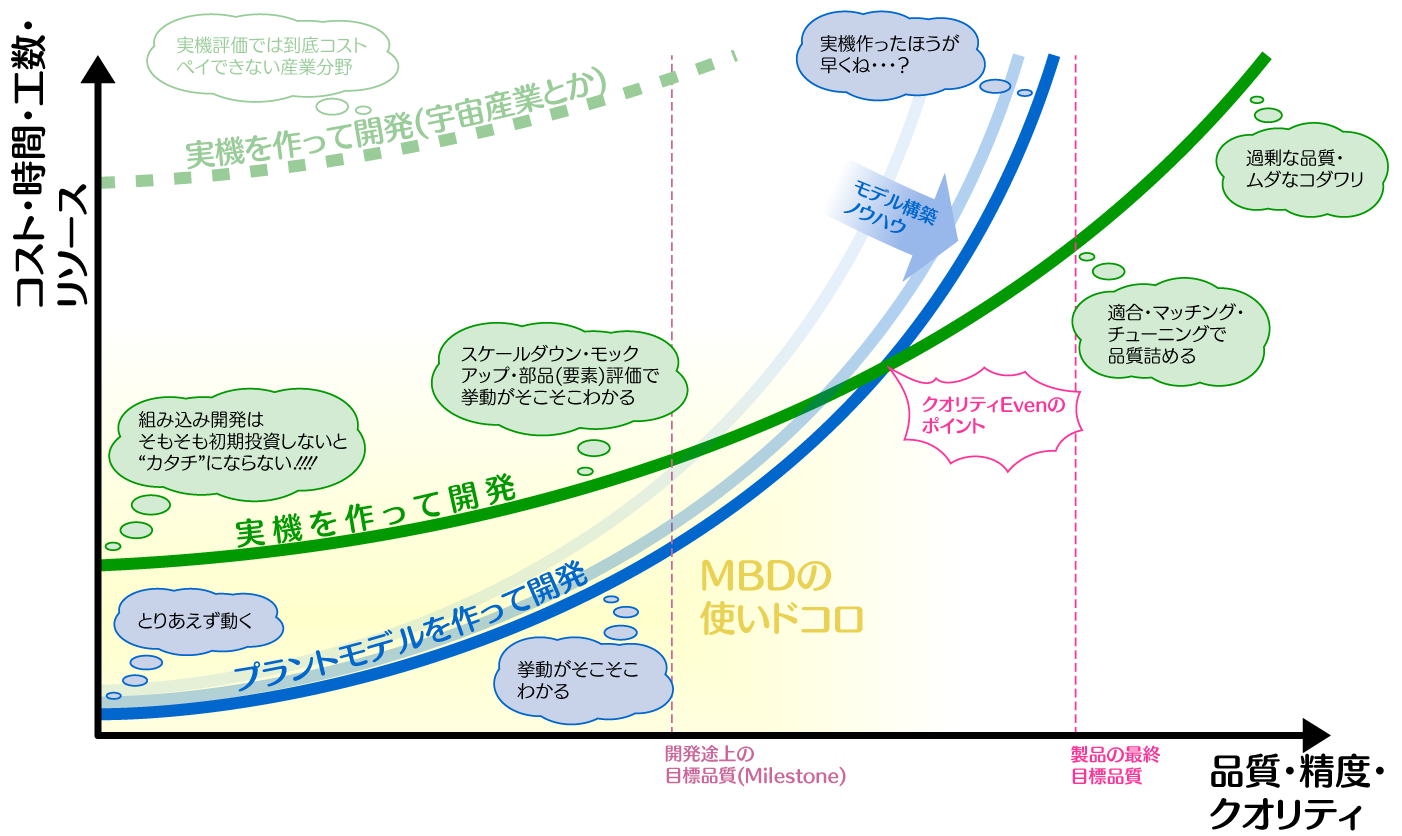
まずは一般的なハナシとして、品質(クオリティ)あげるためには、多くのリソース投入⁹が必要です。そして、モノづくりに関わっている多くの皆さんが経験上わかっている通り、これらは比例関係ではなく指数関数的(高度な品質を上げるためには莫大なリソースが必要)だと思います。それを踏まえた上で以下の概念図をご覧下さい。

これは、私が考える「MBDの使いドコロ」を表したグラフで、横軸に「クオリティ」縦軸に「リソース」を取って、「実機を作って開発(緑線)」するのと「プラントモデルを作って開発(青線)」するときの関係を比較して描いたものになります。一枚の絵にごちゃごちゃ描いてしまったのでわかりづらいですが、言いたいことは以下です。

• 実機を作って開発するためには、そもそも初期(スタートアップ)に多くのリソースが必要(組み込み系の宿命)
  • 逆にプラントモデルは、少ない初期投資で結果は出る(クオリティはおいといて)
• 製品(作りたいモノ)の最終品質(高レベルな品質要求)まで持って行くには、プラントモデルを使った開発だと逆に多くのリソース投入が必要になる。
• それぞれの曲線が交差する場所がある(クオリティEvenのポイント)。MBDの使いドコロはこのポイントより左下のエリア。
  • たとえば、開発途中の品質確認(最終品質は今は必要ないけど、イケるかイケないか、イケないとしたら何か対策はあるのか？の確認がしたい)などの節目に対して、MBDは有効。
• プラントモデルを使ったモノの作り方ノウハウを積むと、「プラントモデルを作って開発」曲線(青線)は右側に倒れてくる。
  • 最初にMBDを導入して間もなく、青線が垂直に立った状態で費用対効果の評価をするのは時期尚早。
  • ノウハウ・スキルを詰むと青線は右側に倒れてくるけど、「製品の最終目標品質」(赤点線)を越えることはやっぱり難しい。(なぜなら、“プラントモデルの究極の精度目標”がこのライン、つまり“実機とコンパチで同じ挙動”をターゲットにするため)
• 航空宇宙産業など、そもそも「実機を使って評価」曲線(緑線)がはるか上にある分野(実機評価ではコストがかかる分野)ほど、MBDの使いドコロのエリアは広がる。

こんな概念図で示しまたが、残念ながら各曲線の関係やクオリティEvenのポイントなどは、明確に示せないことがほとんど。だからこそ、まずはMBDを試してみて「リソースとクオリティのバランスを見つけながら」うまく自身(または組織)の活用ノウハウとして落とし込めればいいのではないのかなと思います。
今回のお題で言えば、静止摩擦などの「非線形要素」が簡単にモデリング・シミュレートできるので、それによってモノがどのような挙動をするのか？教科書的な制御ロジックだけでイケるのか？イケないとしたらどんな補正ロジックが必要なのか？といった、実機を作る前に かなりの詳細度の制御ロジック(プログラム)検証ができる という点が、電子工作におけるMBDのうま味であり、使いドコロであると思います。寒い場所で走らせたら(フリクションが高くなったら)どうなる？みたいな環境変化のシミュレーションも気軽に試せますしね。

おわりに

今回の記事では、プラントモデルを中心にMBDのうま味について解説してみました。
ちまたのMBDにまつわる情報リソースを見回してみると、たとえばSURIAWASE2.0をはじめとして、どれも「MBDの利活用&連携方法」についてばかりで、「そもそもMBDとは何？」とか「MBDって何ができて、何ができないの？」みたいな素朴だけど本質的な疑問に答えてくれる情報がなかなかありません。
この理由について考えてみると、MBDを語るには...

1. 「設計」「CAE」「実験」(+プロジェクトマネジメント)といった、開発プロセス方向にまたがる概念
2. 「機械」「電気」「熱流体」「化学反応」「制御(ソフトウェア)」といった、工学分野(ドメイン)方向にもまたがる概念

これらの概念を全部ひっくるめて語らなきゃいけないので、なかなか説明するのにしんどいのは確かです。¹⁰
だからこそ、電子工作という自己完結する題材は、MBDを語るのに(理解するのに)格好の材料であると思います。(ワタシも実際にプラレール魔改造を通して、MBDの理解が深まりました)
みなさんもぜひ、電子工作にMBDを適用してMBDのうま味を肌で実感してみて下さい！！

懺悔

記事のどっか途中に書きましたが、あらためて懺悔します。
今回作ったプラレール車両モデル(プラントモデル)は、実はプラレール車両本体を完成させたあとにモデリングしたものでした。
本来MBDにおけるプラントモデルとは、実機を作る前に検討するために作るものですから、言ってることとやってることが逆なんです。そうです。今回のモデル構築はぶっちゃけこの記事書くネタ用に作ったのが理由の半分でした。
ではあともう半分の理由は？というと、それは・・・甥にあげてしまったあのプラレールでもう一度遊んでみたくなったんです・・・。

OpenModelicaで構築したモデルをFMUで書き出してSimulink側に取り込み、こないだ作ったコントローラモデルとつないでCo-Simulationした様子。
プラレール本体なくても、全然遊べる！(謎) pic.twitter.com/vMi1rwcxF5

— わたなべ (@mana_544) January 29, 2020

こうなるといよいよモデルを作ることが目的になってしまっているので、ワタシは1D-Simプラントモデル沼にどっぷりとハマってしまったようです。
みなさんはぜひ心得を忘れずに、沼にハマらぬようお気を付け下さい。MBDとはたいへん便利で魅力的なモノではあるのですが、MBDに限らずバーチャルの世界は現実世界を忘れるので、ホントにコワイですね...

---

1. かといって、プラントモデルは「早く・安く・うまく」作れるものでもないので、さじ加減というのが本当にムズカシイのですけれど。 ↩

2. そのぐらい、物理現象のシミュレーションというのはそもそもの計算コストが高いと言うことです。 ↩

3. ワタシはコッチの世界(3D-CAE)は門外漢だから、間違っていたらツッコミお待ちしてます。 ↩

4. ただまぁ、別にいついかなる時でも「1Dマルチドメイン非因果系モデリング is best solutionだぜ！」なんていうワケではなく、ようは「どんな挙動を捉えたいか？」によって、選択をすれば良いと思います。今回のプラレール車両モデルの例では、作りたい(検討したい)内容が「発進時の静止摩擦に打ち勝つための電圧補正プログラムを検討したい」としているので、関心事は「どんな電圧(電気ドメイン)をかけたら、プラレールは動く(直線運動ドメイン)のか？」となります。そこで選択肢としては「物理分野(ドメイン)を跨いでるし、“静止摩擦・動摩擦”みたいな非線形要素も考慮したい。だけど、要素分布ほど詳細な検討はいらない。じゃあ、1Dマルチドメイン非因果系モデリングでやるのがベストだろうなぁ。」といった具合です。 ↩

5. 各ツールとも、それぞれ出自(分野)の異なるトコロからマルチドメインシミュレーション対応化していったので、まさに現在は群雄割拠といった状態です。正直、何選べばいいのかワカラン。ただ一つ言えることは、OpenModelica以外は有料で、軒並み趣味で買える値段じゃねぇ(Simscapeは趣味ライセンスがあります(飲み会約1回分)) ↩

6. Simscapeという製品を別途購入すれば、Simulink上で非因果系モデリングが可能になります。 ↩

7. そもそも1D-CAEをやったことのない人からすると「何を言ってるん？」というような内容だと思いますが、「物理現象をコンピュータに解かせる(微分方程式の数値解法)」ってそれはそれは大変なことで、本来はそれだけで本が数冊書けるような、そんな奥深い世界です(沼です)。これはつまり、ただ単に「挙動を確認したい」だけなのに、相当に高度な特殊スキルをカンストレベルまで積まないと「シミュレーションができない」というのが常識でした。非因果系モデリングというアプローチは言うなれば、ちょっとの特殊スキルレベルで「シミュレーションができる」ようになるチートアイテムといったところでしょうか。 ↩

8. OpenModelicaでFMU Ver.2.0 Co-Simulationに対応したのは、つい最近のバージョンからのようです。ワタシが使っているのは1.14.1です。 ↩

9. ここでは、人・モノ・カネ・時間など、“モノを作る”上で必要なあらゆる材料(ISO9001風にいうと「資源」)概念を包括してリソースと呼んでいます。 ↩

10. だいたいMBDの解説というと、「V字プロセス」を持ってきて語る場合が多いですが、組み込み製品の開発プロセス全体をそもそも俯瞰してみたことがない人は(特に実務者)、V字プロセス自体がピンとこない人も多いです。なので、この記事ではV字プロセスの引用は避けています。 ↩