More than 5 years have passed since last update.

全天球イラスト作画補助ツール(パースガイド生成)を作った話

Posted at 2019-07-15

はじめに

今年(2019年)5月28日に開催されました MATLAB EXPO Japan 2019のLightning Talkイベントに 「お絵描きでMATLAB使ってます」 というネタで登壇し、MATLAB擬人化キャラ(MathWorks非公認)を披露して、いろんな意味で インパクトを与えてしまいました。

この記事では、ライトニングトークでご紹介させていただいたMATLABスクリプトについて、小ワザ(荒ワザ)解説を行いたいと思います。

そもそも何のスクリプトなの？

当日の発表資料をリメイクして公開しましたので、そちらをご覧下さい。¹

ライトニングトーク発表スライド(リメイク版)

上記スライドを見ていただければこのスクリプトが何かが分かると思いますが、ヒトコトで言うと、全天球イラストを描く時に必要となるパースガイドを自動で計算&生成してくれるツールになります。絵を描くための補助ツールですね。
しかし今改めて思うと、もしかしたら絵を描く以上にこのスクリプトは作るのタイヘンだったかもしれません。

MATLABサンプルコード

こちらがそのスクリプトになります。(長いので折りたたんでます)

horzperspecguide.m

function horzperspecguide()

% ベース Object Pointの定義
baseAz = 180.0;
baseOP_D = 20.0;
baseOP_W = -40.0;
baseOP_HList = [-100, -60, -20, 20, 60];
% Width グリッド間隔の定義
widthDivision = 5.0;
widthCount = 13;
% Depth グリッド間隔の定義
depthDivision = 10.0;
depthCount = 11;
% ファイル名のプレフィックス
filename = 'PG';
% 書き出しPNGサイズ(ヨコ, タテ)
canvas_width = 5376;
canvas_height = 2688;
% パースガイド線の太さ
guideline_width = 5.0;

% pixcelでキッチリ描き出す用の設定
ppi_unit = 72;
cpi_unit = 2.54;

% HeightList毎に画像生成
for i_HList = 1:length(baseOP_HList)
    fprintf('H = %.1f\n', baseOP_HList(i_HList));
    % baseオブジェクトPointの構造体を生成
    baseOP = struct('D', baseOP_D, ...
                    'H', baseOP_HList(i_HList), ...
                    'W', baseOP_W, ...
                    'baseAz', baseAz, ...
                    'Az', NaN, ...
                    'Ev', NaN);
    % 色の決定
    % 明度(v)は0.5~1.0
    color_v = 0.5 + i_HList * (0.5/length(baseOP_HList));
    % 色相(h)は黄金角から決定
    golden_ang = 360 * (1-1/((1 + sqrt(5)) / 2));
    color_h = mod(golden_ang * i_HList, 360) / 360;
    color_rgb = hsv2rgb([color_h, 1, color_v]);
                
    % figureの生成
    fh = figure('PaperPositionMode', 'manual', ...
                'PaperSize',[canvas_width * cpi_unit / ppi_unit, canvas_height * cpi_unit / ppi_unit], ...
                'PaperPosition', [0, 0, canvas_width * cpi_unit / ppi_unit, canvas_height * cpi_unit / ppi_unit], ...
                'InvertHardcopy', 'off');
    ah = axes('Color', [0 0 0], ...
         'XColor', 'none', ...
         'YColor', 'none', ...
         'XLim', [0 360], ...
         'YLim', [-90 90], ...
         'Position', [0 0 1 1]);
    hold on
    % ヨコ線描画(ヨコ線の本数 = depthCount)
    for j = 0:depthCount
        
        D = baseOP.D + j .* depthDivision;
        H = baseOP.H;
        W = linspace(baseOP.W, widthCount * widthDivision + baseOP.W, 100);
        % Az, Ev変換
        [Az, Ev] = DHW2AzEv(D, H, W, baseOP.baseAz);
        
        % plot
        plot(ah, Az, Ev, 'Color', [1 1 1], 'LineWidth', guideline_width);
        
    end
    % タテ線描画(タテ線の本数 = widthCount)
    for j = 0:widthCount
        
        D = linspace(baseOP.D, depthCount * depthDivision + baseOP.D, 100);
        H = baseOP.H;
        W = baseOP.W + j .* widthDivision;
        % Az, Ev変換
        [Az, Ev] = DHW2AzEv(D, H, W, baseOP.baseAz);
        
        % plot
        plot(ah, Az, Ev, 'Color', [1 1 1], 'LineWidth', guideline_width);
        
    end
    
    % figureの一時保存
    print('_tmp', '-dpng', sprintf('-r%g', ppi_unit));
    
    hold off
    close(fh)
    
    % さっき保存した画像を読み込む
    A = imread('_tmp.png');
    
    % イメージサイズを取得
    [h, w, ~] = size(A);
    
    % 色で塗りつぶす
    R = uint8(zeros(h, w)) + color_rgb(1) .* 255;
    G = uint8(zeros(h, w)) + color_rgb(2) .* 255;
    B = uint8(zeros(h, w)) + color_rgb(3) .* 255;
    I = cat(3, R, G, B);
    
    % イメージAをアルファチャンネルとして書き出し
    imwrite(I, sprintf('%s(%g).png', filename, baseOP_HList(i_HList)), 'Alpha',A(:,:,1)); 
    
    
end

disp('パースガイドを全て生成しました。')

function [Az, Ev] = DHW2AzEv(D, H, W, baseAz)
%DHW2AzEv 直交座標系[D, H, W]から球面座標系[Az, Ev]の変換
% [Az, Ev] = DHW2AzEv(D, H, W, baseAz)
% [arguments]
% D : 1x1 or 1xN double
%     奥行き。単位は任意(ただしH,Wとあわせる)
%     Wが1xN double の場合、Dは1x1 doubleにする。
% H : 1x1 double
%     高さ。単位は任意(ただしD,Wとあわせる)
% W : 1x1 or 1xN double
%     横幅。単位は任意(ただしD,Hとあわせる)
%     Dが1xN double の場合、Wは1x1 doubleにする。
% baseAz : 1x1 double
%     基準方位角。[deg]
% 
% [returns]
% Az : 1xN double
%     水平角。[deg]
% Ev : 1xN double
%     仰角。[deg]

Az = baseAz + atand(W ./ D);
hyp = sqrt(D .^ 2 + W .^ 2);
Ev = atand(H ./ hyp);

mファイルで保存すればそのまま実行いただけます。
作ったMATLABバージョンはR2017b(macOS 10.13 High Sierra)ですが、簡単なスクリプトなので、OS, ソフトバージョン問わず動くと思います。
変数で設定値定義した部分の値を変えれば様々なパースガイドを作れますが、リリース目的で作っておりませんので、エラーハンドリングはおろか、なんだったらまともなテストすらしてません。あくまでもサンプルコードとして見てください。
それでは、そんなMATLABコードの小ワザ･･･というか苦労話について解説していきたいと思います。

正距円筒図法(Equirectangular)と座標変換

正距円筒図法(Equirectangular)は、全天球イラストのコアとなる知識です。
当日のLT発表では時間の都合上「描くのがムズい」のヒトコトで片付けてしまいましたが、もう少しだけ解説をしますと、正距円筒図法とはそもそもは世界地図の投影法で「横2:縦1のキャンバスに正方グリッドを描いて、横軸を水平角、縦軸を仰角に対応²させて全射したもの。」となります。
しかし、描き始め当初は当然そんなこと知る由もなく「全天球イラストを描くにあたって、まずはこの“正距円筒図法”なるものを調べよう！」と息巻いたワタシは、数学的な解釈を求めていろいろと探し回ったあげく、最終的にたどり着いたのが アメリカ地質調査所のガチ作図マニュアル³ という謎の超展開に至りました。あたしゃあイラストを描きたいんだよ この文献自体は正距円筒図法のみならず、そこからVRビューへの変換式(Azimuthal Projection)もバッチリ書かれてて、すげぇいい資料なんだけどさ！
そんなわけで、なるべくかみ砕いて(絵描きの視点で)全天球イラストの描き方を解説したものをPixivに投稿したので、よろしければそちらも併せてご覧頂ければと思います。
ここでは、パースガイド生成スクリプトで使ってるMATLABへの実装について少しお話しします。

function [Az, Ev] = DHW2AzEv(D, H, W, baseAz)
%DHW2AzEv 直交座標系[D, H, W]から球面座標系[Az, Ev]の変換
% [Az, Ev] = DHW2AzEv(D, H, W, baseAz)
% [arguments]
% D : 1x1 or 1xN double
%     奥行き。単位は任意(ただしH,Wとあわせる)
%     Wが1xN double の場合、Dは1x1 doubleにする。
% H : 1x1 double
%     高さ。単位は任意(ただしD,Wとあわせる)
% W : 1x1 or 1xN double
%     横幅。単位は任意(ただしD,Hとあわせる)
%     Dが1xN double の場合、Wは1x1 doubleにする。
% baseAz : 1x1 double
%     基準方位角。[deg]
% 
% [returns]
% Az : 1xN double
%     水平角。[deg]
% Ev : 1xN double
%     仰角。[deg]

Az = baseAz + atand(W ./ D);
hyp = sqrt(D .^ 2 + W .^ 2);
Ev = atand(H ./ hyp);

座標計算のコードはこの部分ですが、ヒトコトで言ってしまえば、三次元直交座標 $(x, y, z)$ から球面座標 $(r, \theta, \phi)$ への座標変換をやっているだけです(距離rは使いませんが)。そしてMATLABにはそれを一発で実現してくれる cart2sph というそのものズハリな関数が用意されているのですが、ワタシの考える"向き"(座標系)と違ったので⁴ イチから実装しました。といっても、逆三角関数とピタゴラスの定理を使った簡単な式です。
また、引数 D と W のどちらかは配列(行ベクトル)を取り、その各要素ごとに座標変換処理をするのですが、こんなときに便利なのが ベクトル・行列化による演算 です。
他プログラミング言語経験者の方は、ついforループを書きたくなりますけど、MATLABで高速処理させたいなら、いちど既存のプログラミング言語のforの使い方(要素ごとに処理する発想)は捨て去り、全部丸ごと計算する発想(ベクトル・行列化)にアタマを切り替える必要があります(このアタマの切り替えがなかなか結構ムズい)。 ⁵

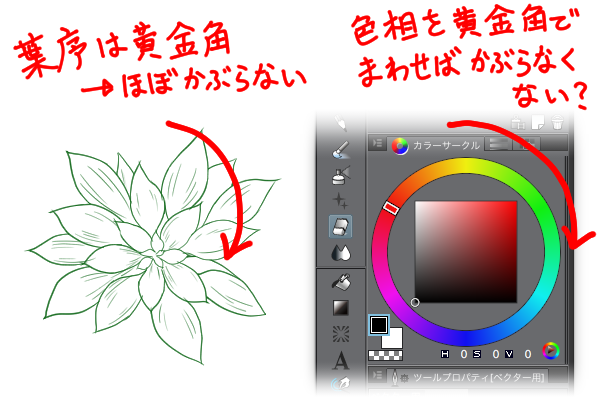
なるべく色がかぶらないように、いろんな色で書き出す

複数枚のパースガイドを書き出すときに、識別しやすいようにパースガイドに色をつけていますが、なるべく色がかぶらないように自動で色を決定しています。式にするとこんな感じです。

\alpha = 360 \times \left( 1 -  \frac{2}
{ 1 + \sqrt{5} } \right)

h = 
    \begin{array}{lr}
      (i \alpha)  \bmod  360  & (i = 1 , 2 , \ldots) 
    \end{array}

$\alpha$は黄金角と呼ばれる定数、$h$は色相$(0 \le h < 360)$を表します。ヒントは**植物の葉っぱ(葉序)**から得ました。
植物は効率的に光合成をするためになるべく葉っぱ同士が 太陽光を遮らないように葉をつける そうで、その角度はフィボナッチ数で表現できるそう(まじか！)。というわけで、そのフィボナッチ数から導き出される「黄金角」で色相環をぐるぐるすればほぼかぶらないんじゃない？と思いついたわけです。

    % 色の決定
    % 明度(v)は0.5~1.0
    color_v = 0.5 + i_HList * (0.5/length(baseOP_HList));
    % 色相(h)は黄金角から決定
    golden_ang = 360 * (1-1/((1 + sqrt(5)) / 2));
    color_h = mod(golden_ang * i_HList, 360) / 360;
    color_rgb = hsv2rgb([color_h, 1, color_v]);

実装は、色相 color_h は黄金角ずつずらし、明度 color_v は50%～100%に段々とあげるように書き出しています。彩度は100%固定(色はつけたいので)。色相・彩度・明度で色を求めたら、hsv2rgb関数でRGB値に変換しています。(画像書き出しはRGB値指定なので)

任意のピクセルサイズでFigureを画像書き出し

座標変換で計算した水平角と仰角のリストをplot関数でFigureにプロットして、printで画像に書き出しますが、“任意のピクセルサイズ”で書き出すのにちょっと手こずりました。
全天球イラストはVRビューの解像感の関係から、そこそこ大きいキャンバスサイズ⁶ で描く必要があり、パースガイドもこのキャンバスサイズにピッタリあわせたいので、任意のピクセル指定で書き出したいのです。
最初、figureオブジェクトのUnitsプロパティに'pixels'を指定すればpositionでいけんだろハハハなんて思ってたのですが、高解像度ディスプレイ⁷ だったり、ディスプレイサイズを遙かに超えるピクセルサイズで書き出したい場合にどーにもうまくいきません。
なので、Figureオブジェクトのプロパティに以下を指定します。

% 書き出しPNGサイズ(ヨコ, タテ)
canvas_width = 5376;
canvas_height = 2688;

ppi_unit = 72;
cpi_unit = 2.54;

    % figureの生成
    fh = figure('PaperPositionMode', 'manual', ...
                'PaperSize',[canvas_width * cpi_unit / ppi_unit, canvas_height * cpi_unit / ppi_unit], ...
                'PaperPosition', [0, 0, canvas_width * cpi_unit / ppi_unit, canvas_height * cpi_unit / ppi_unit], ...
                'InvertHardcopy', 'off');

まずは画面解像度を72ppiと仮定して⁸、そこからPaperUnitsが'centimeters'(規定値)なので、指定ピクセルになるように書き出しサイズを[cm]へと逆算してPaperSize, PaperPositionを指定してます。

    % figureの一時保存
    print('_tmp', '-dpng', sprintf('-r%g', ppi_unit));

そして、書き出すときに print関数の解像度指定オプションを利用して、 sprintf('-r%g', ppi_unit) こんな感じで(さっき指定した)72ppiの解像度で書き出すという荒技をしています。

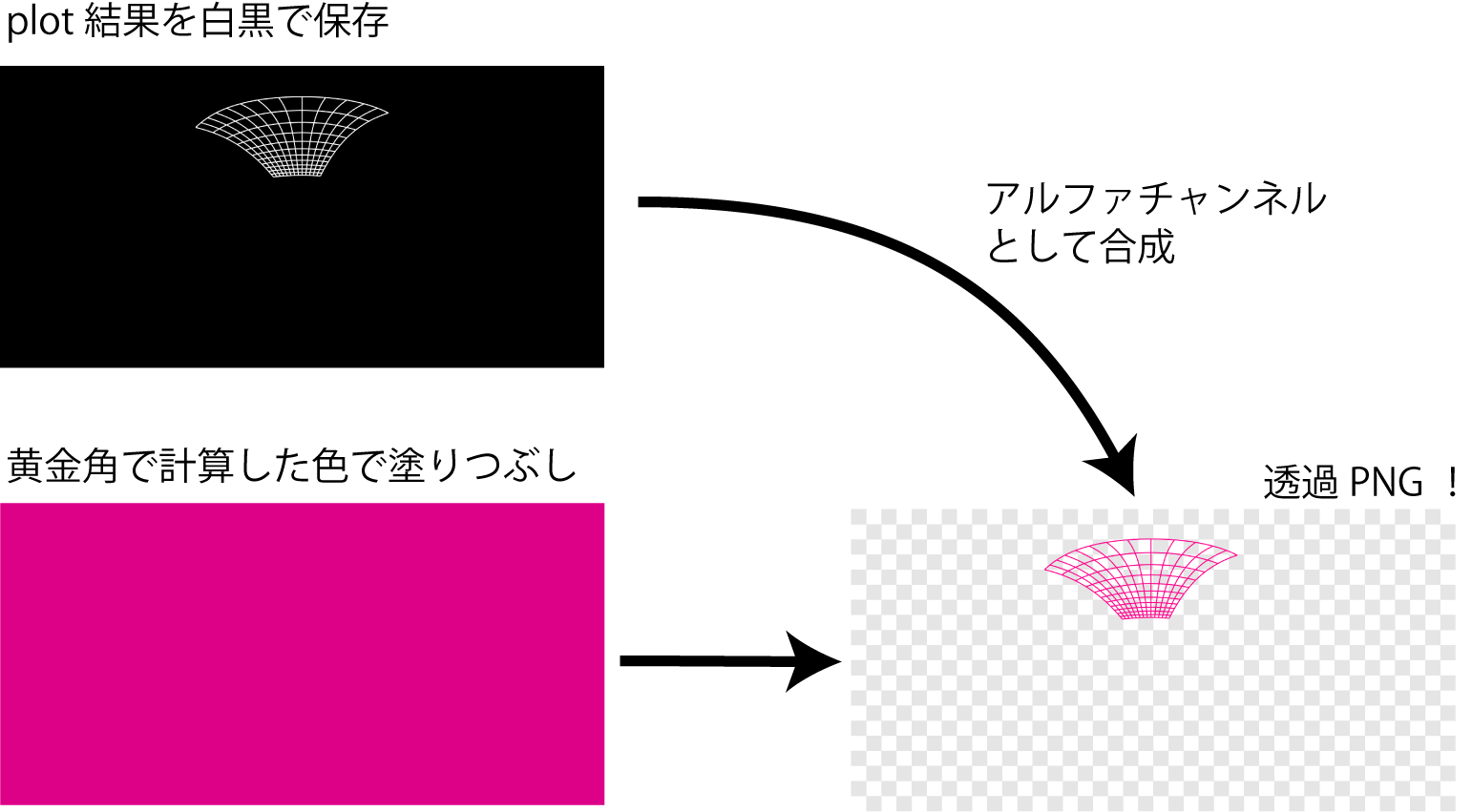
透過PNGの生成

書き出したパースガイドたちは、ペイントソフトにレイヤーとして重ねて表示するので、plotライン以外(背景)は透明にしたいです。しかしMATLABのprintではPNG書き出しはできるものの、グラフの透過指定ができません。
そこで目を付けたのが、 imwrite関数にあるPNGオプション(アルファチャンネル指定)。

    % figureの一時保存
    print('_tmp', '-dpng', sprintf('-r%g', ppi_unit));
    
    hold off
    close(fh)
    
    % さっき保存した画像を読み込む
    A = imread('_tmp.png');
    
    % イメージサイズを取得
    [h, w, ~] = size(A);
    
    % 色で塗りつぶす
    R = uint8(zeros(h, w)) + color_rgb(1) .* 255;
    G = uint8(zeros(h, w)) + color_rgb(2) .* 255;
    B = uint8(zeros(h, w)) + color_rgb(3) .* 255;
    I = cat(3, R, G, B);
    
    % イメージAをアルファチャンネルとして書き出し
    imwrite(I, sprintf('%s(%g).png', filename, baseOP_HList(i_HList)), 'Alpha',A(:,:,1));

いちどfigureの背景を黒、plotラインを白でprint書き出した後、その画像をimreadで再度読み込み、アルファチャンネルとしてimwriteで書き出すことで、透過PNG画像の書き出しを実現するという荒技を繰り出しています。カラーチャンネルは先ほど黄金角から求めた色で全ピクセルを塗りつぶした行列を作成します。

おわりに

お絵描きにMATLAB使ってるヤツなんているわきゃないと思ってるので、こんなの誰得スクリプトだよとは思いますが、一つ一つの小ワザやアイデアが、皆さんのMATLABを使う際のアイデアの種となれば幸いです。

当日のLT発表をご覧いただいてない方でもわかるように加筆修正を施しました。あと当日のスライドはKeynoteで作りましたが、Prezi使ってみたかったのでこれを機にリメイクしました。 ↩
地図で言うところの、水平角(Azimuth)=経度、仰角(Elevation)=緯度に相当します。 ↩
John, P. S. (1987) "Map projections: A working manual" U.S. Geological Survey Professional Paper 1395, pp. 90–91 ↩
ワタシが考えている座標系は「全天球イラストの描き方【用語解説】」に載せています。 ↩
ファイルI/O処理など、forを使わないといけない場面ももちろんあります。 ↩
私の場合、5376 x 2688[px] で描いてます。 ↩
MacのRetinaディスプレイ等を指します。 ↩
書き出し時の解像度と一致していれば良いので、72ppi以外に設定してもOKです。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up