本日の内容
LTSpiceのラプラス変換を使い、任意のトリガ遅延と幅を持ったパルスを作る方法を記す。
ただし、長くなったので今回は途中まで。
目次
- 対象読者
- 作りたいもののイメージ
- 想定用途
- 教科書的な矩形単発パルスのラプラス変換表現
- 入力信号を矩形単発パルスに変換する伝達関数
- ラプラス変換表現・失敗例
- LTSpiceが遅い原因
- LTSpiceでのラプラス変換表現・一歩前進
対象読者
大学の信号処理とか制御工学の授業でラプラス変換勉強して
よく分からないままに単位だけとって、研究とか仕事で使ったこと無かった人。
ラプラス変換は手計算で展開するのがつらいです。
mathematica等の数式処理ソフト類で、ラプラス変換動かした経験が無い人は、教科書だけ読んでもピンとこないと思います。
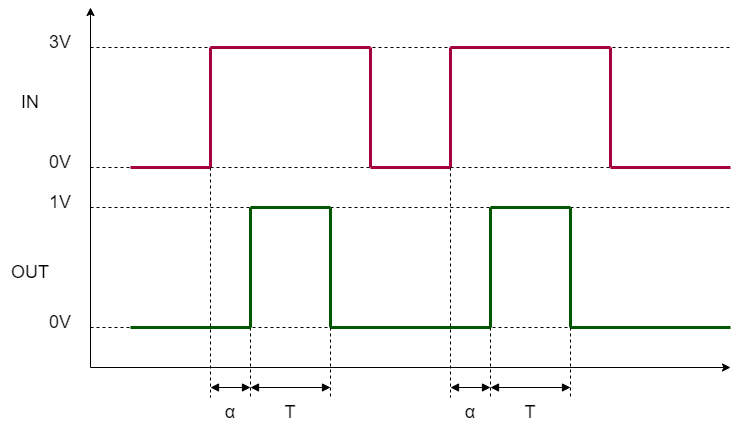
作りたいもののイメージ
下記波形イメージを参照。
入力波形の立ち上がりエッジから、α遅延した、幅Tの波形を作る
想定用途
- 波形の立ち上がりエッジ検出をしたい。
- マイコンリセット解除に伴う突入電流をLTSpiceで表現したい(電源につける最適なコンデンサ容量検討)
教科書的な矩形単発パルスのラプラス変換表現
ラプラス変換表は検索しても良いし、大学時代の教科書を引っ張り出してきてもいいのでそっちを見て下さい。
一番手っ取り早いのはwikidpediaでしょうか。
Wikipedia ラプラス変換
トリガからα遅延して幅Tの矩形単発パルスをラプラス変換で表す
ラプラス変換表よりステップ応答を表す$1/s$と遅延を表す$e^{-\tau s}$を組み合わせて
\begin{align}
F(s) &= e^{-\alpha s} \times \frac{1}{s} - e^{-\alpha s} \times e^{-T s} \times \frac{1}{s}\\
F(s) &= e^{-\alpha s} \times \frac{1-e^{-T s}}{s}
\end{align}
と記述できます。
遅延αのステップ応答を遅延(α+T)のステップ応答で打ち消す式を立て、見やすいように整理した形です。
ここで注意が必要なのは、導出した式F(s)は伝達関数ではなく
最終出力(前掲図OUT相当)の波形を表した式という事です。
入力信号を矩形単発パルスに変換する伝達関数
出力波形を表す式は導出できたので、伝達関数を導出します。
教科書によくある表現をすると出力を$Y(s)$、入力を$U(s)$とした下式の$G(s)$を導出します。
\begin{align}
Y(s) &= G(s) \times U(s)
\end{align}
変形すると
\begin{align}
G(s) &= \frac{Y(s)}{U(s)}
\end{align}
なので入力信号$U(s)$をラプラス変換した式を立てれば導出できる訳です。
話を単純にするため、求める入出力関係イメージ図最初の1発目立ち上がりエッジ近傍を拡大します。
時刻0で入力された信号に時間α遅延して、幅Tのパルスが出力される形となっています。
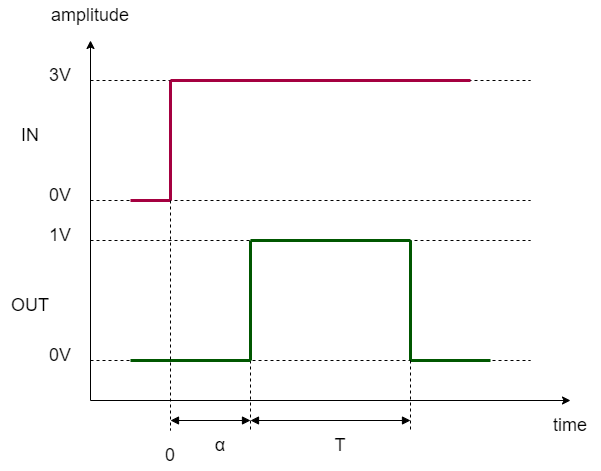
つまり、想定する入出力系において入力信号はステップ応答の一種と解釈できるわけです。
入力を$U(s)=\frac{1}{s} $と表すと、伝達関数$G(s)$は
\begin{align}
G(s) &= \frac{Y(s)}{U(s)} \\
&= \frac{e^{-\alpha s} \times \frac{1-e^{-T s}}{s}}{\frac{1}{s}} \\
&= e^{-\alpha s} \times \frac{\frac{1-e^{-T s}}{s}}{\frac{1}{s}}\\
G(s) &= e^{-\alpha s} \times (1-e^{-T s})
\end{align}
と表せます。
ラプラス変換表現・失敗例
求めた伝達関数をLTSpiceの任意電圧源 or 任意電流源のlaplace式でそのまま表しても上手く行きません。
具体例を示します。
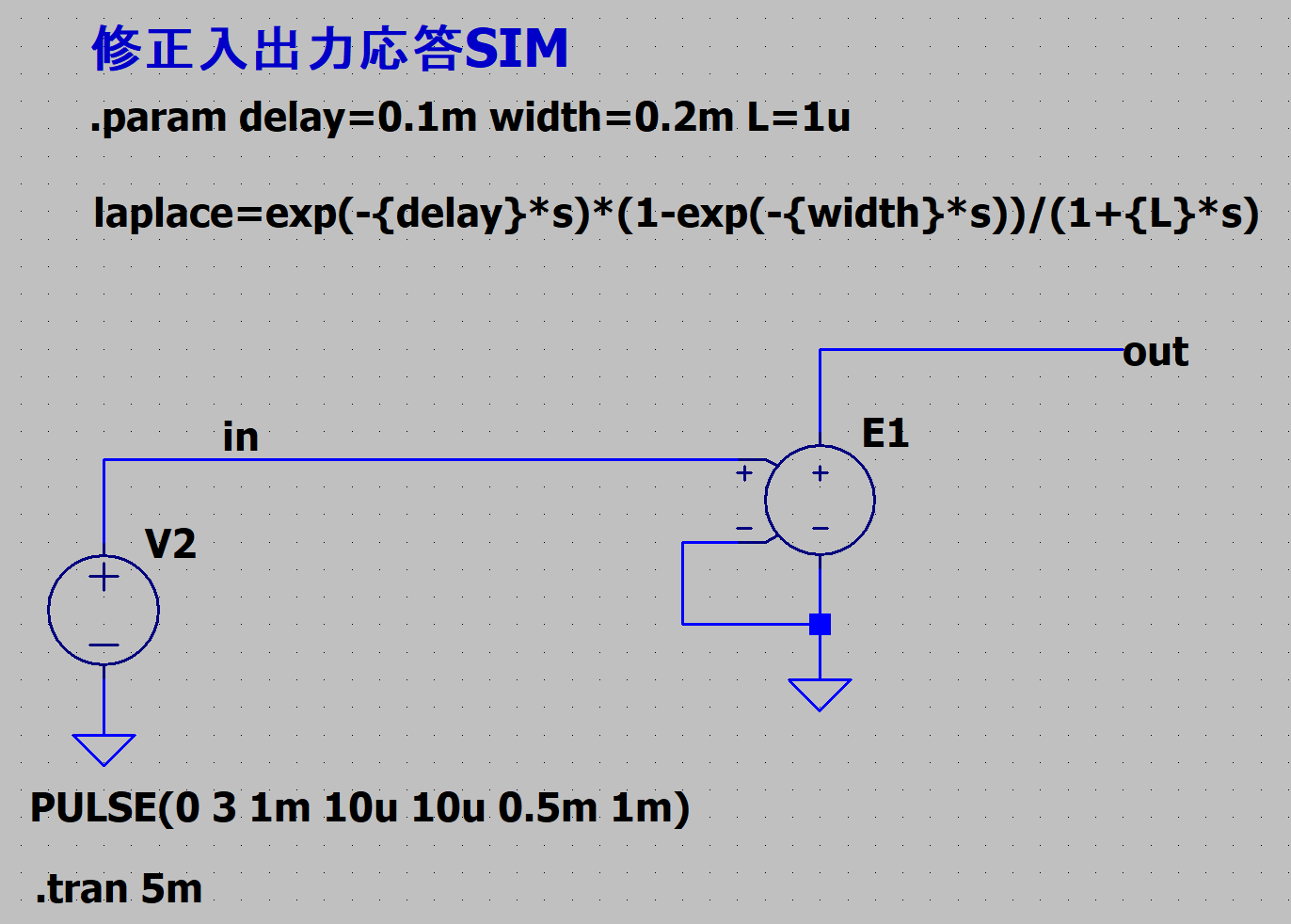
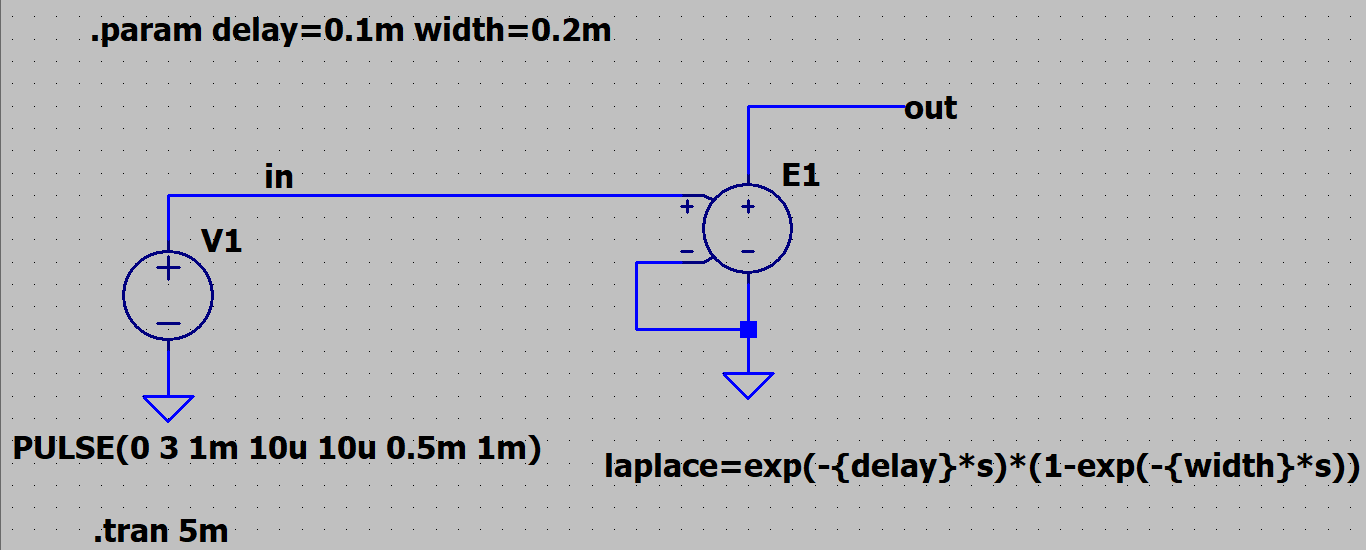
V1は判別したい信号源です。0-3Vの1kHz矩形波です。
E1は電圧制御電圧源です。入力電圧に適用する伝達関数
laplace=exp(-{delay}*s)*(1-exp(-{width}*s))
を記述します。
後からチューニングできるようにするため、前述の遅延αをdelay、幅をwidthパラメータとして記述しています。
値は例なので深い意味はありません。
過渡解析で5msec間のSIMしようとした途中経過がこちらです。

1秒辺りで進むSIM時間がたったの666nsecです。
たかだか1kHzの入力信号を、伝達関数一個通すだけのSIM 5msec分過渡解析するのに2時間以上かかります。
つまり、現実的な時間で結果を得るためにLTSpiceへ突っ込む式としては不味いわけです。
LTSpiceが遅い原因
原因は伝達関数を通って出力される信号のスルーレートが高すぎる事です。
前述したように欲しい出力信号$F(s)$のラプラス変換式にはステップ応答の項が含まれています。
\begin{align}
F(s) &= e^{-\alpha s} \times \frac{1-e^{-T s}}{s}
\end{align}
つまり、理論上スルーレート無限大の部分が含まれる波形ということです。
数学上は連続関数として扱えても、LTSpiceは現実を扱う数値解析です。
N回目の計算結果とN+1回目の計算結果が、そこそこ滑らかに連続していると見なせる精度まで
時間分解能を細かく計算する必要があり、許容できない時間がかかっています。
よって、解決策はSIM結果を眺める人間が必要十分な時間分解能でもSIMが収束するよう
伝達関数のスルーレートを下げることです。
一番お手軽なのはラプラス変換的に1次LPFをかけること。
こういう式変形です。
\begin{align}
F'(s) &= F(s) \times \frac{1}{1+L \times s} \\
F'(s) &= e^{-\alpha s} \times \frac{1-e^{-T s}}{s} \times \frac{1}{1+L \times s}
\end{align}
Lはおなじみの時定数です。次節で適当な時定数の大きさを考えます。
LTSpiceでのラプラス変換表現・一歩前進
前述した例で、必要十分な時間分解能を考えます。
周期1kHzの信号を0.1msec遅延させ、幅0.2msecの信号を観察したい訳です。
0.1msecオーダーの信号を観察するのに、悪影響が十分小さな時定数なら実用上問題ない訳です。
よって、興味のある時間分解能オーダーの$\frac{1}{100}$~$\frac{1}{1000}$程度の時定数のLPFをかけることにします。
幅を持たせているのは、SIM結果を眺める人間の趣味と使えるマシンパワー等の兼ね合い次第の部分があるためです。
修正したのが下記回路図
時定数は1usecとしました。
修正前と比較して時間当たりのSIM進捗は約2000倍になっています。
お手軽に5msec程度をSIMするにはちょうど良い塩梅です。
| SIM進捗状況スクリーンショット | |
|---|---|
| 修正前 |  |
| 修正後 |  |
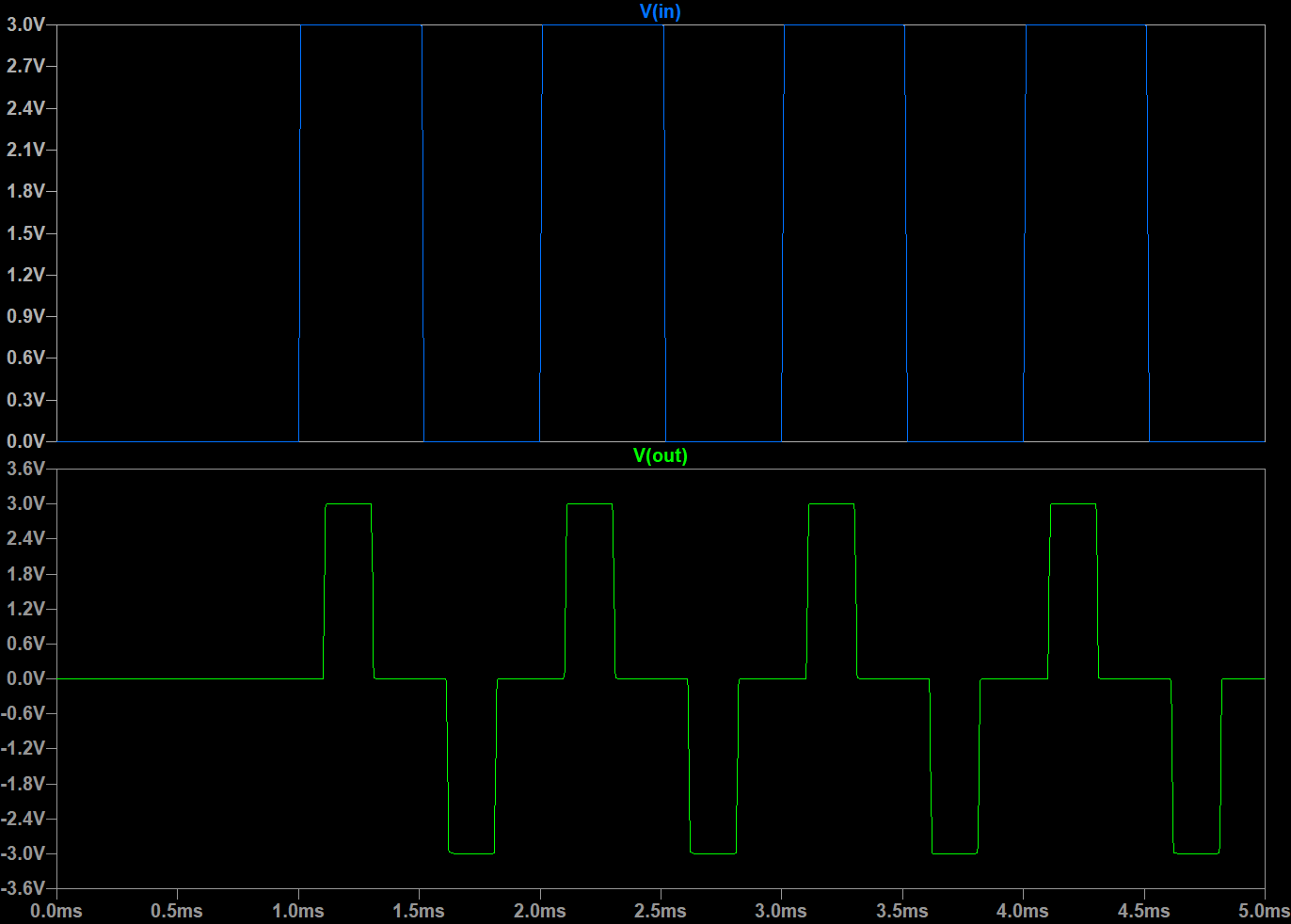
パラメータで設定した通り、入力信号の立ち上がりに同期して、
0.1msecの遅延、0.2msec幅のパルスが出力されて居ますが、入力信号の立ち下がりにも反応しています。
また、出力振幅も最初に提示した出力イメージ図より大きいです。
この問題の対処は記事が長くなってきたので次回。