More than 5 years have passed since last update.

AtCoderの「ABC081B - Shift only」をShift Onlyで解こうとしたらビット演算で計算量を削減していた話

Posted at 2018-07-31

TL;DR

ABC081-B「Shift Only」を解いてみた記事は数多くあるけど、「Shift Only」というタイトルに着目してシフト演算で解こうとしている記事が見当たらなかった
シフト演算だけで解けないか考えた結果、ビット演算とシフト演算を利用することで時間計算量・空間計算量を削減する解法に行きついた

Introduction

はじめまして。malbare666と申します。
普段はSIerでインフラエンジニア見習いの日々を過ごしており、毎日泣きながら残業をしています。悲しいね。
仕事でコードを書く機会がなく寂しいので、競技プログラミングに手を出してみることにしました。

AtCoderに登録し、「初心者がまずやってみるべき問題10選」とされているAtCoder Beginners Selectionを解いてみたのですが、4問目「ABC081B - Shift only」を愚直に解いたところでふと思いました。

「タイトルがShift only……ということは『シフト演算だけで解いてみろや』というのが問題の本当の趣旨ということ……？」

ということで**「シフト演算を有効活用して問題をかっこよく解こう！」と思いながらあれこれ試行錯誤していた結果、「ビット演算で計算量を減らせる！」**という（当初のもくろみとは外れた）気付きが得られましたので書きます。
初歩的な問題ではありますが、「プロコンで解き方を工夫するのは楽しい！」と初心者が感じた一例としてお読みいただけたらと。

この記事の流れについて

公式解説の解法をで解いてみる
この記事の本題である「ビット演算・シフト演算」で解いてみる
1.と2.の解法について、計算量の観点から比較評価してみる

前提知識について

以下の点については知識がある前提で記事を進めていきます。それぞれについては参考リンクも貼りますので適宜ご参照ください。

計算量(空間計算量、時間計算量)
- 参考リンク : 計算量
ビット演算、シフト演算
- 参考リンク : ビット演算入門 - Qiita

1. 公式解説から考える解法

公式の解説では、以下の2つの方針が紹介されています。

黒板に書いてある整数を管理しておいて，「書かれている整数がすべて偶数である限り」「書かれている整数すべてを 2 で割る」をシミュレートすればよいです．
あるいは，ほとんど同じことですが，最初書かれている整数それぞれに対して「最大で何回 2 で割れるか」を求め，その最小値をとってもよいです．

この方針に従って素直に実装していくと以下の通りになります。

公式解法1 : 操作シミュレート

黒板に書いてある整数を管理しておいて，「書かれている整数がすべて偶数である限り」「書かれている整数すべてを 2 で割る」をシミュレートすればよいです．

とのことなので、愚直にやっていきます。

#include <iostream>
using namespace std;

int main(int argc, char const *argv[])
{
  int N,A[200],ans=0; // N,A : 問題文通りの定義 / ans : 答え
  cin >> N; // Nを格納

  for (int i = 0; i < N; ++i)
  {
    cin >> A[i]; // A_1～A_Nの入力をA[0]～A[N-1]に格納
  }

  ans=0; // 操作可能回数は0回からスタート
  while(1){
    bool allEven = true; // 全て偶数かどうかのフラグ

    for (int i = 0; i < N; ++i) // 黒板の数字すべてについて
    {
        if(A[i]%2==1){ // A[i]が奇数ならば終了
            allEven = false;
            break;
        }else{ // A[i]が偶数ならば2で割って再代入
            A[i] /= 2;
        }
    }

    if(!allEven){ // 奇数が含まれていた場合 => 操作可能回数を増やさず終了
        break;
    } else{
        ans++; // 全て偶数だった場合 => 操作可能回数を+1する
    }

  }

  cout << ans << endl; // 答えを出力
  return 0;
}

公式解法2 : それぞれの割れる回数の最小値を取る

あるいは，ほとんど同じことですが，最初書かれている整数それぞれに対して「最大で何回 2 で割れるか」を求め，その最小値をとってもよいです．

とのこと。こちらも素直にやっていきます。

#include <iostream>
using namespace std;

int main(int argc, char const *argv[])
{
  int N,A,ans; // N,A : 問題文通りの定義 / ans : 答え
  cin >> N; // Nを格納
  ans = 1000; // 最終的な答えは最小値なので、まずはどんな答えよりも大きい数字を代入

  for (int i = 0; i < N; ++i)
  {
    cin >> A; // A_iをAに格納
    int tmpAns = 0; // A_iに対する「最大で何回 2 で割れるか」の値。最初は0

    while(A%2 == 0){ // Aを2で割れるかぎり
        tmpAns++; // 割れる回数を+1して
        A = A / 2; // Aには2で割った数値を再代入
    }

    if (tmpAns < ans){ // tmpAnsがansより小さければansに代入 →ansはtmpAnsの最小値となる
        ans = tmpAns;
    }
  }

  cout << ans << endl; // 答えを出力
  return 0;
}

2. ビット演算とシフト演算で考える解法

さて、ここからが本題です。
問題タイトルにある「Shift only」という文言から、**「ビットシフトを駆使するとよりカッコよく解けるのでは？」**と思いを巡らせたところ、A₁～A_Nをビット列として考えることで、以下のように問題文を翻訳できることに気付きました。

黒板に N 個の~~正の整数~~ ビット列 A₁,…,A_N が書かれています．
すぬけ君は，黒板に書かれている整数 ビット列がすべて偶数 (最下位ビット=0)であるとき，次の操作を行うことができます．

黒板に書かれている整数すべてを，~~2 で割ったもの~~ 右に1ビットシフトしたものに置き換える．

すぬけ君は最大で何回操作を行うことができるかを求めてください．

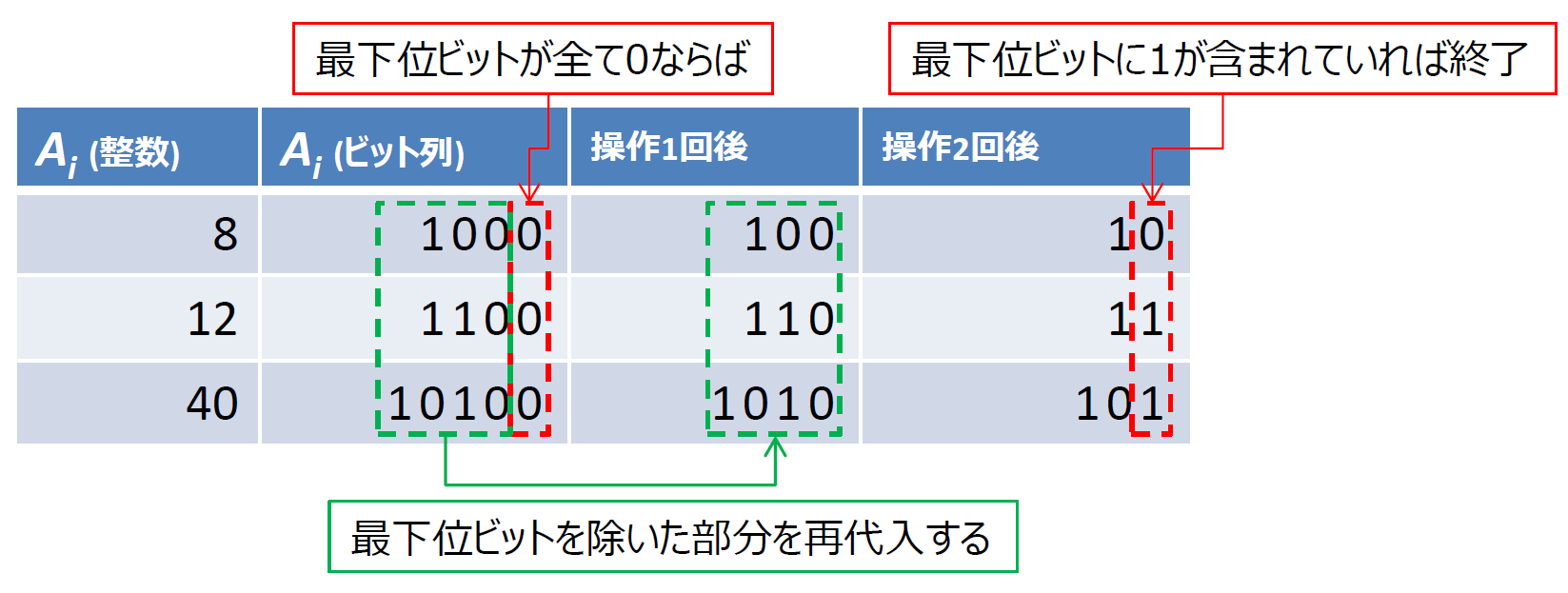
具体的な問題を例に考えてみます。入力例に挙げられている「8, 12, 40」の場合を考えてみます。

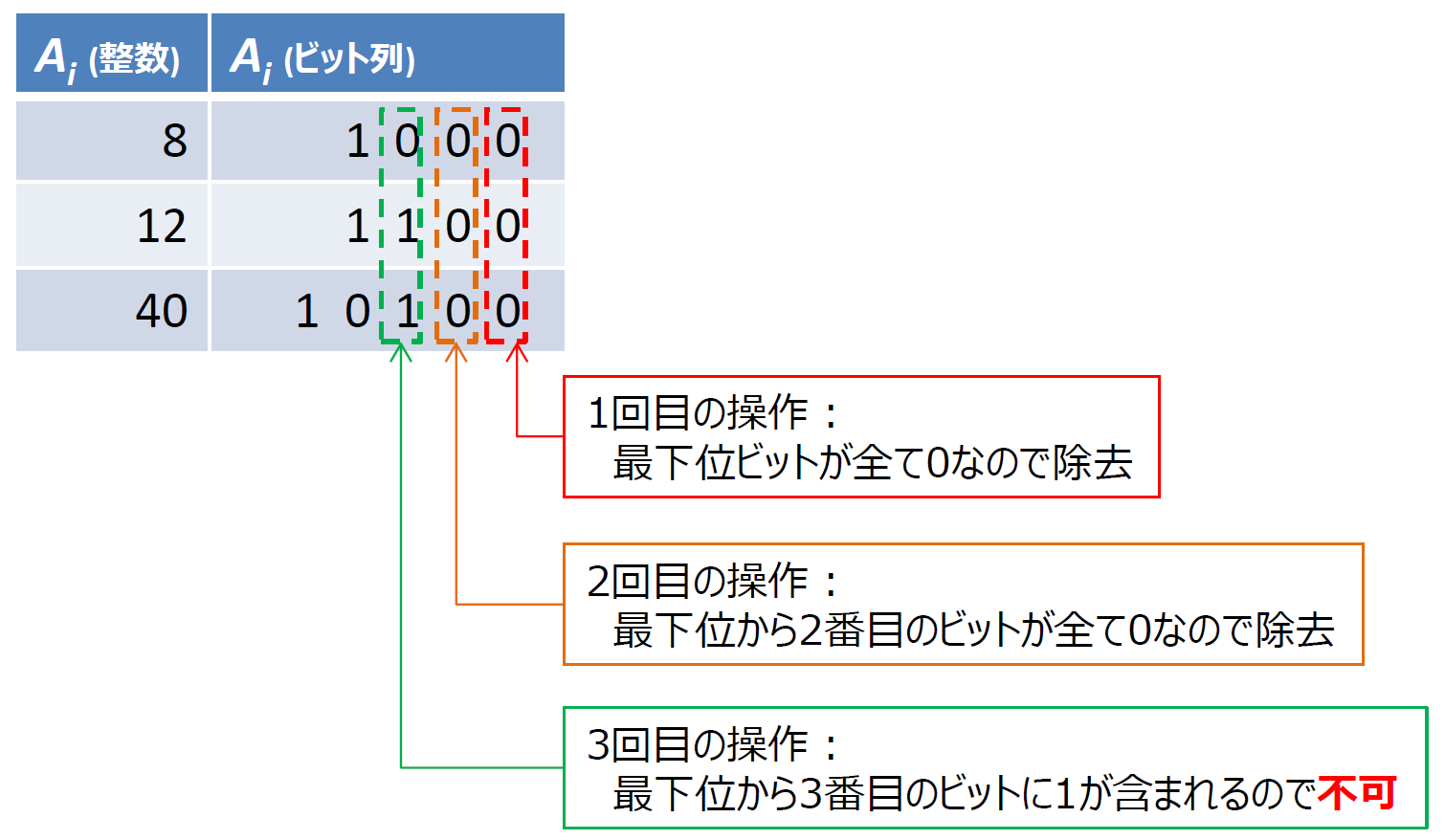
さらに、**「偶数を右に1ビットシフトする」 = 「最下位ビットを取り除く」**と解釈できることを考えると、下図のように発展できます。

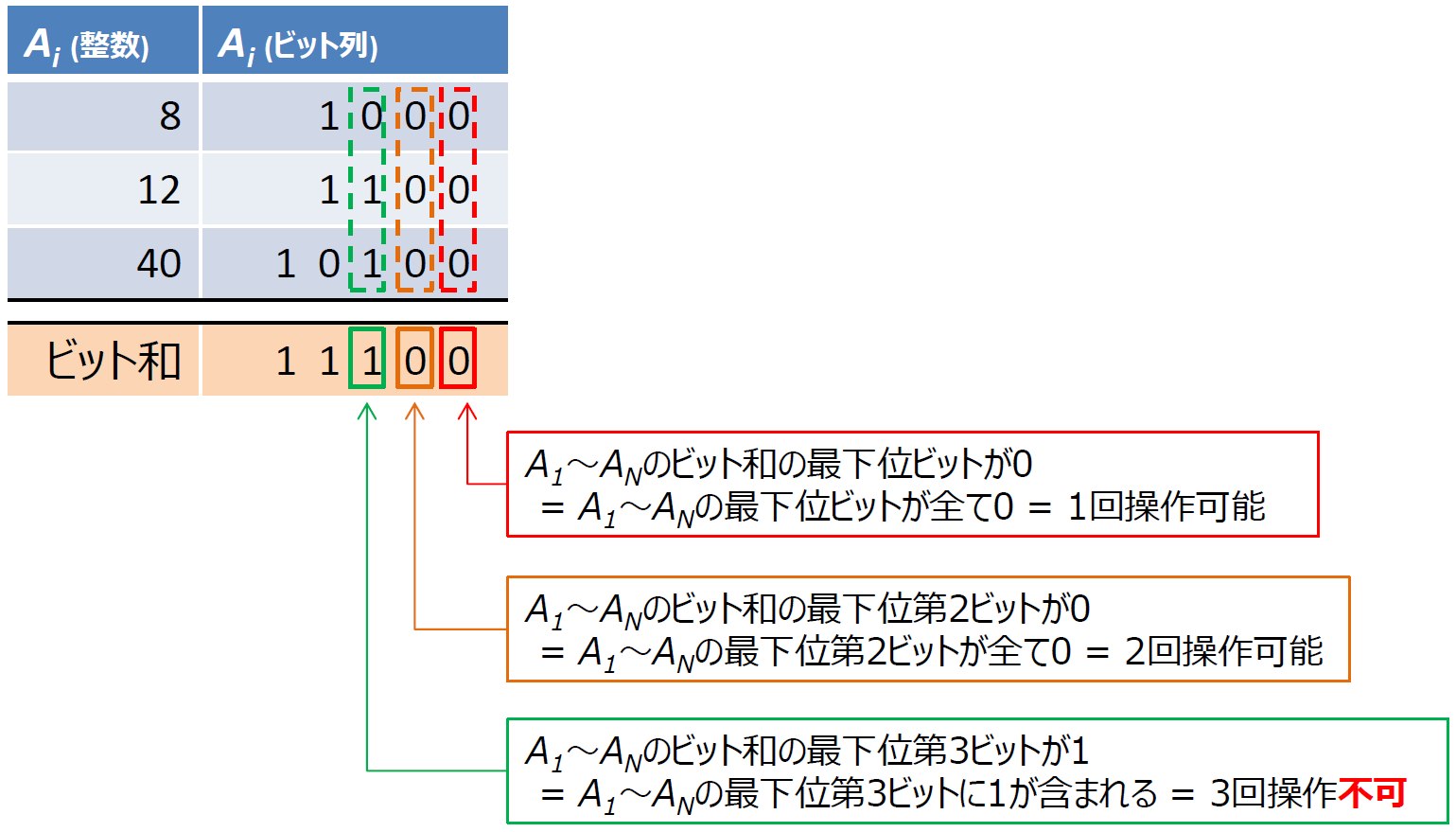
ここでさらに、「A₁～A_Nの第nビットが全て0である」=「A₁～A_Nのビット和の第nビットが0である」ということを考えると、最終的に以下の所まで持っていくことができます。

ここまでいったら後はコードにしてみます。以下のように書けます。

#include <iostream>
using namespace std;

int main(int argc, char const *argv[])
{
  int N,A,b=0,ans=0; // b : ビット和
  cin >> N;

  for (int i = 0; i < N; ++i)
  {
    cin >> A; // A[i]を格納
    b = (A | b); // bはA_1～A_Nのビット和
  }

  while((b&1)==0){ // ビット和の最下位ビットが0である限り
    b = b>>1; // ビット和を右に1ビットシフトして
    ans++; // 操作回数を1回増やす
  }

  cout << ans << endl;
  return 0;
}

短くなった！ちゃんと通った！

3. 計算量を評価してみる

それではここで、公式の解法と今回の解法の計算量を見ていきます。
入力件数$N$, 操作可能回数$M$を用いて、各解法で書いてきたコードでの時間計算量・空間計算量は以下のように考えられます。

解法	時間計算量	空間計算量
公式1 操作シミュレート	$O(N*M)$	$O(N)$
公式2 最小除算回数	$O(N*M)$	$O(1)$
ビット演算シフト演算	$O(N+M)$	$O(1)$

この通り、時間計算量・空間計算量ともに節約することができました。
(※公式解法1,2の計算量は「最も愚直に書いたアルゴリズム」でのオーダーなので、アンフェアであることは否めませんが……)

さいごに

このようにシンプルな問題でも、解き方の工夫によって計算量を減らせるということを学べました。
（この問題では$N$や$M$が微々たる大きさなのでそこまで嬉しいことでもないですが。。。）
今回この解法を考えることで、競プロにおける醍醐味らしきものを感じることができたので、これから様々な問題にチャレンジしていきたいな、という気持ちです。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up