はじめに
実験装置から得た信号から,パラメータを抽出するためにフィッティングを行うことがあるかと思います(頻繁に).一方で,「いざ信号を得たのにやり方がわからない!」という初心者もいらっしゃるのではないでしょうか.事実,私も初めは何をすればいいのやらわからず調べ調べでなんとか出来るようになりました.本稿ではそのクイックスタートと注意点を述べ,さっそく取り掛かれるようにしたいと思います.
用いるデータと解析式
ここでは,汎用性を考えて非線形データを用います.非線形データができれば,線形データは取るに足りません.
(※線形データは別のコマンドでより簡単に行えます)
後にフィッティングを理論式で行うために,今回はローレンツ関数を用います.データを再現する理論式は次式で表されるものとしましょう.
y = S\frac{W^2}{(x-x_0)^2 + W^2} + A\frac{(x-x_0)W}{(x-x_0)^2 + W^2}
ここで,
$S$ : 対称ローレンツ関数の係数
$A$ : 反対称ローレンツ関数の係数
$x_0$ : $x$方向のずれ
$W$ : 信号の線幅(半値半幅)
とします.
これらが求めたいパラメータです.
いざフィッティング
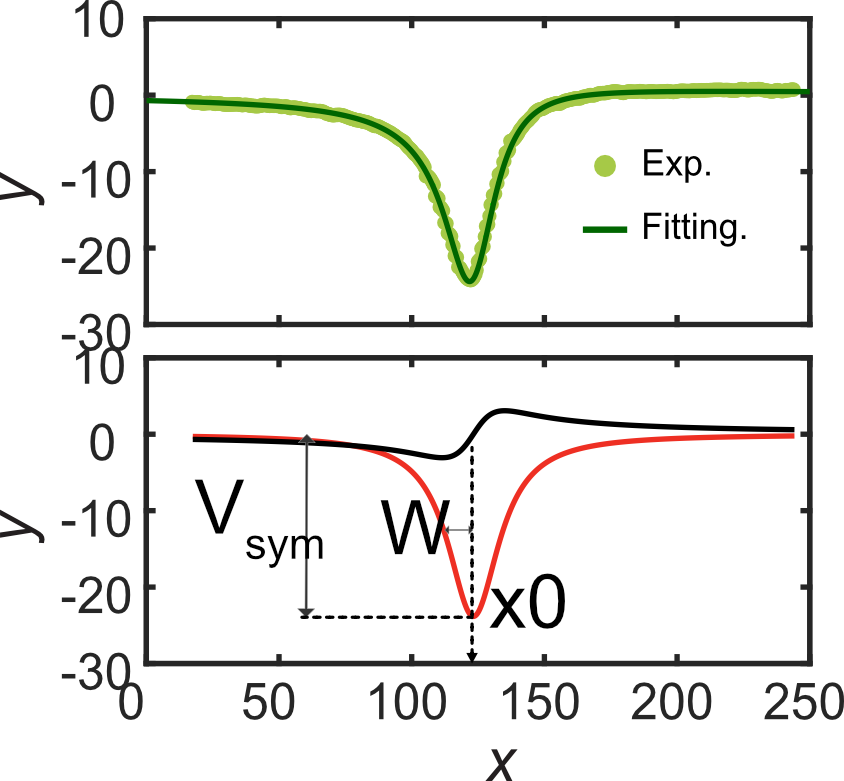
フィッティングした結果を下に示しました.
上の図が,実験データとそのフィッティング.
下の図は,フィッティングデータをさらに分解したものです(理論式を参照).
このように,任意の関数について,理論式があれば基本的になんでもフィッティングすることができます.
ただし,フィッティングの方式(LM法など),フィッティングの開始点の有無にもよってもその可否が決まってしまうため,適宜パラメータを調節する必要があります.
コード
以下に用いたコードを示します.
clc
clear all
# データのインポート
data = dlmread('4171003-12.txt100mW-7.0GHz.txt');
# データの前処理
N_data=size(data,1);
N_data1_end = N_data/2-N_data1_start;
N_data2_start = N_data/2+N_data1_start;
N_data2_end = N_data-N_data1_start;
for i = N_data1_start : N_data1_end
x1(i-N_data1_start+1) = data(i,1);
y1(i-N_data1_start+1) = data(i,2)*1e+6;
end
x1 = x1';
y1 = y1';
for j = N_data2_start : N_data2_end
x2(j-N_data2_start+1) = data(j,1);
y2(j-N_data2_start+1) = data(j,2)*1e+6;
end
x2 = x2';
y2 = y2';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%フィッティング形式の設定
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
f1 = fitoptions('Methods','NonlinearLeastSquares',...
'StartPoint',[10 -50 40 10 0],...
'Algorithm','Levenberg-Marquardt')
f2 = fitoptions('Methods','NonlinearLeastSquares',...
'StartPoint',[10 50 -40 10 0],...
'Algorithm','Levenberg-Marquardt')
%フィッティング式
ft1 = fittype('S*W^2/((x-H_res)^2+W^2)+A*((x-H_res)*W)/((x-H_res)^2+W^2)+Y','options',f1);
ft2 = fittype('S*W^2/((x-H_res)^2+W^2)+A*((x-H_res)*W)/((x-H_res)^2+W^2)+Y','options',f2);
%フィッティングされるパラメータの確認(一度確認すればなくても良い)
coeff = coeffnames(ft1)
%フィッティング.引数に(x1,y1),フィッティング形式にft1などとする.
[curve1] = fit(x1,y1,ft1)
[curve2] = fit(x2,y2,ft2)
%フィッティングされたパラメータをparameter1, 2に格納.
parameter1 = coeffvalues(curve1);
parameter2 = coeffvalues(curve2);
%フィッティングパラメータを取り出し.
H1_res = parameter1(2);
S1 = parameter1(3);
A1 = parameter1(1);
W1 = parameter1(4);
Y1 = parameter1(5);
H2_res = parameter2(2);
S2 = parameter2(3);
A2 = parameter2(1);
W2 = parameter2(4);
Y2 = parameter2(5);
データの前処理は,データ形式によって方法が異なるでしょう.
MATLABで用いるフィッティングでは,x, yをリスト形式で持っておけば"fit(x,y,ft)"によって無事に行えます.
得られたパラメータを用いて,グラフにするなりするのはより簡単に行えるでしょう〜