記事をご覧いただきありがとうございます!
感想やご指摘があればコメントいただけると幸いです!
(この記事は英語の発音記号(特にアクセント)を意識してカタカナを書いてあります。例としては
アクセント → アクセント (ˈəksɛnt)
コメント → コメント (ˈkɑmɛnt)
などです。)
0. 問題設定
教師あり学習を考えます. つまり以下のような設定です:
『$D=(x,y)^{n}\in{(\mathbb{R}^{d_x}\times\mathbb{R}^{d_y})} ^n\in\mathbb{D}$が与えられた際,
$x$から$y$を予測する学習機を作りたい.』
近年では,様々な学習機(モデル)があり,
勾配ブースティング木,深層学習,パラミターが小さめの統計モデルなどがあります.
この記事ではそれらの詳細には触れませんが,
精度を上げるためのスタッキングという技術の精度保証について考察していきます.
1. スタッキング (ˈstækɪŋ)
スタッキングとは,
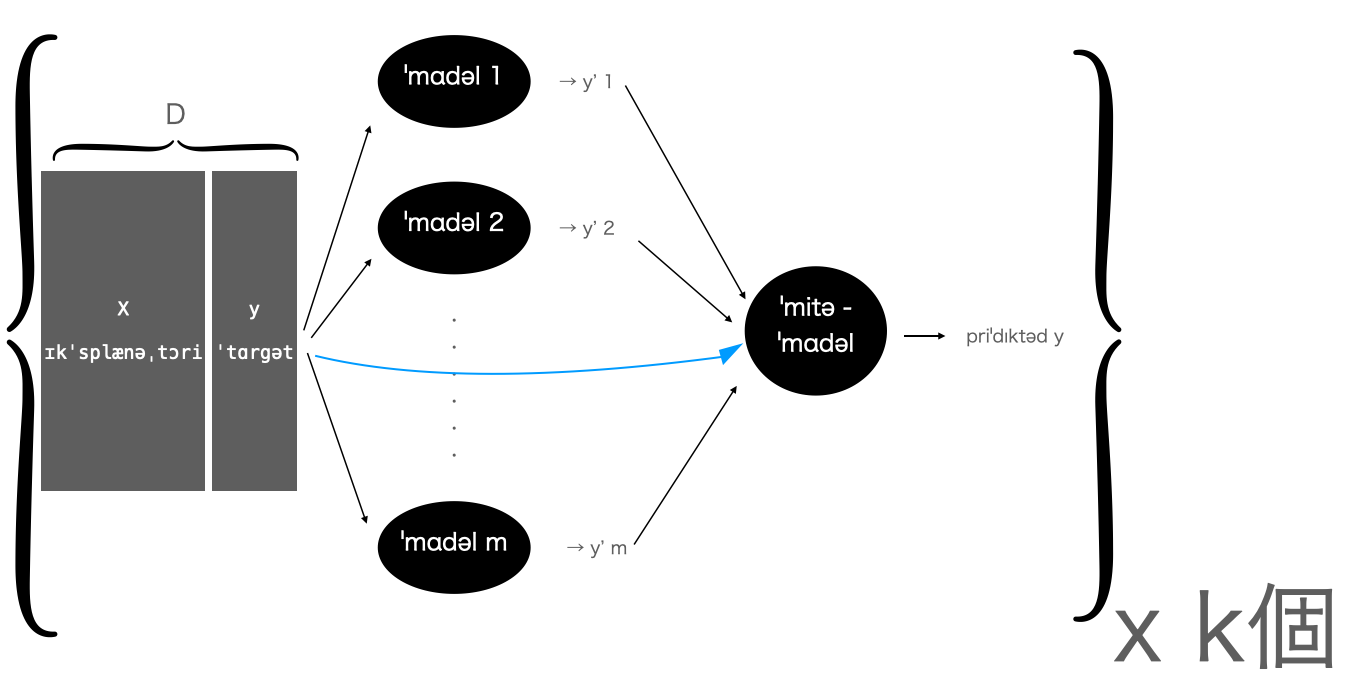
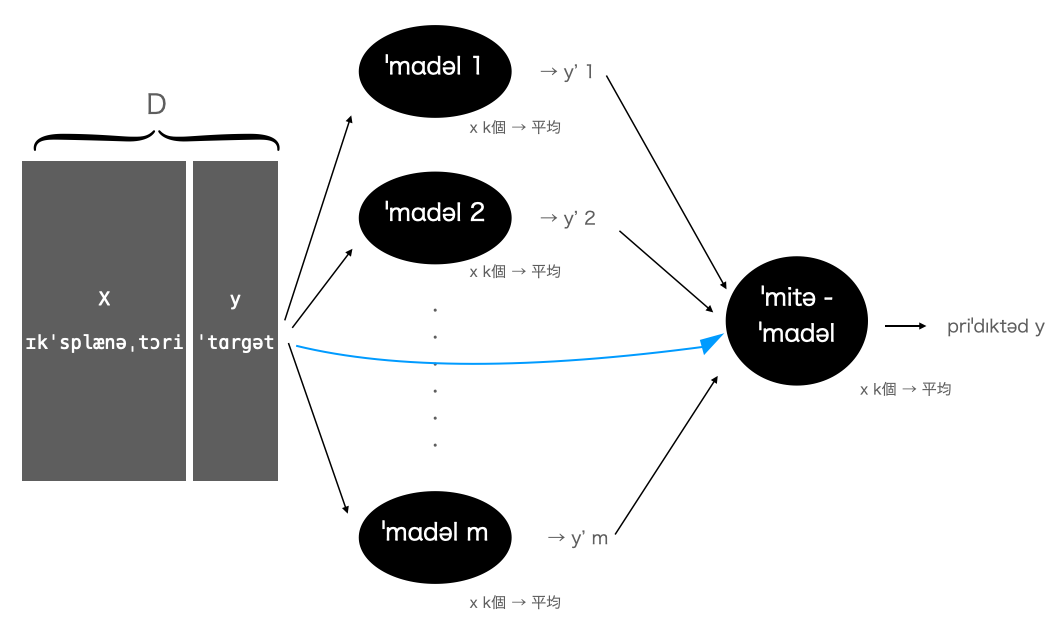
複数のモデル(m個)の出力値を入力値として別のモデル (ミタ・モデル)で再度学習して予測する技術のことです.
イミジとしては以下の通りです:

(上記の水色の矢印は0である場合も多いと思います.ただ,人間社会の会議や意思決定では水色を入れて考えることが一般的な気がします.)
この手法はとても良く機能しますが,実装や理論を少し間違えるとデイタ・リ-ケジ(ˈdeɪtə ˈlikəʤ)が起きてしいまい,正しい精度保障ができなくなってしまいます.
そのため,この記事では,精度保証とデイタ・リ-ケジに注目してスタッキングを紹介します.
精度保証とは,現在$D$に含まれていないデイタに対しても当てはまりをよくするということです.それを保証する量としてしばしば使われるのが,汎化誤差です.
2. 汎化誤差 (ˌʤɛnrəlɪˈzeɪʃən ˈɛrər)
汎化誤差とは,様々な定義の仕方がありますが,真のデイタの分布に対して当てはまりの良さの数値として定義されます(分布のKL情報量から算出する方法やある損失関数に関する期待値に関して計算する方法など).
今回は,ある損失関数($L(y,y)$)の期待値として定義します.デイタ$D$が与えられた際の学習機$f$の損失関数は以下で定義されます:
$$
G(f,D)=\mathbb{E}_{(x,y)}[L(f(x|D),y)].
$$
ここで注意したいのが,
- $D$に関する期待値は取らない(A)
- $(x,y)$の分布は未知(B)
ということです.
上記のことからk フォウルド・クロス・ヴァリデイションという指標を汎化誤差の代わりに用いることが多いです.
3. k フォウルド・クロス・ヴァリデイション (krɔs - ˌvæləˈdeɪʃən)
k-クロス・ヴァリデイションとはデイタ$D$を$k$個に分割して汎化誤差を近似的に見積もる手法です.
分割の仕方($cv$)は様々ありますが,総じて以下のように定義されます:
\begin{align}
CV(f,D,cv,k)=\frac{1}{k}\sum^{k}_{i=1}\frac{1}{|cv(D,i,{\rm valid})|}\sum_{(x,y)\in cv(D,i,{\rm valid})}L(f(x|cv(D,i,{\rm train})),y).
\end{align}
ここで,$cv:\mathbb{D}\times Int \times Str \rightarrow \mathbb{D}$として分割を与える関数です.イミジとしては以下の通りです:
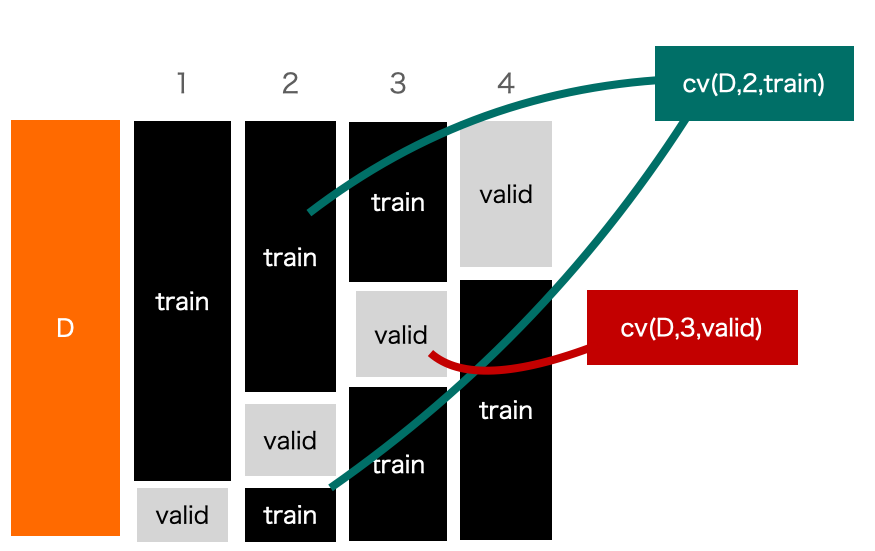
これが汎化誤差を近似した値と言える根拠は,validに対して(cvを考慮して)期待値を取ると汎化誤差に一致するためです(*):
\begin{align}
\tilde{\mathbb{E}_{{\rm valid}}}[CV(f,D,cv,k)]=\frac{1}{k}\sum^{k}_{i=1}G(f,cv(D,i,train)).
\end{align}
(*:一部,学習機ではearly stoppingやtarget encodingなどの手法を用いる関係上,多少のvalidationのdata leakageを許容する考えもあり,現実社会では厳密に期待値を取っても一致しない状況が多いと考えられます.)
ここで注意したいのが,
汎化誤差の際にも言及した(A)の$f(x|D)$の$D$に対して期待値を取らないことにあります.
逆に言えば,$f$の条件付きパラメータ(f(・|×××)のxxxの部分)に期待値を取るデイタを含めてはならないということです.
これに注意してスタッキングを考えます.
4. スタッキングにおけるcvを考える
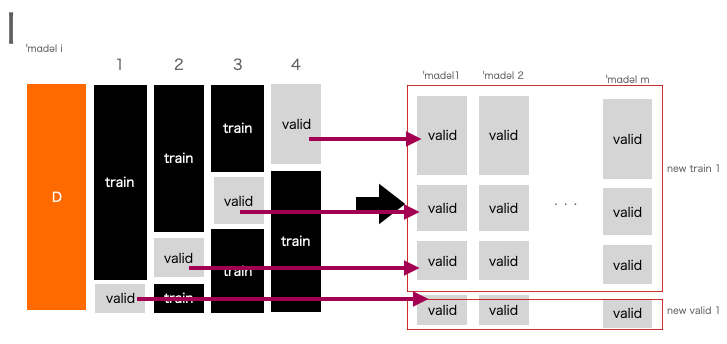
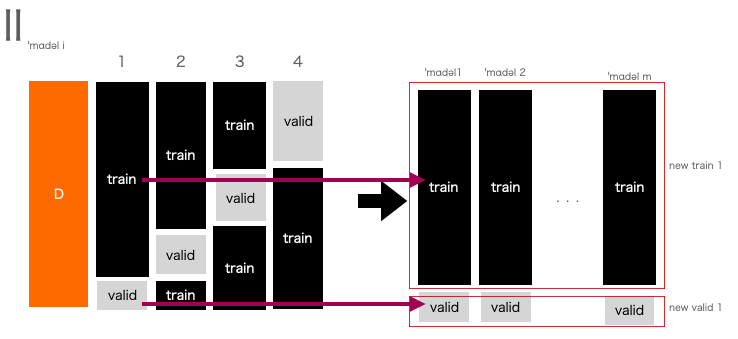
スタッキングにおけるcvでは以下の二つのケースを私は考えました:
- それぞれのモデルでcvをして実装をした後,最後にそれらをスタッキングをする(I).
- スタッキングまでをcvをする(II).
イミジとしては以下の通りです(以下のtrainやvalidはその部分データに対応する出力値が入っていると考えてます):
さて,どちらが数学的にスタッキングの精度保証を行うことができるでしょうか.
まず,IIが正しいことは直ちにわかります.
というのも,new validに対して期待値を取ろうとしてもその情報が学習機の学習に用いられていないためです.
しかし,Iは正しくありません.
というのも,Iにおけるnew validに対して期待を取ろうとすると,スタッキング前のcv(2,3,4)でそれらのvalidのデイタを元に学習を行なっているからです.つまり,期待値を取ろうとすると,うまく計算できないことがわかります.
よって,スタッキングの実装で精度を保証するにはIIの方法を用いる必要があります.
4.1. 実際は...?
しかし,実用上はどうでしょうか.
直感的には,Iでも上手くいく気もしますが,私には良くわかりません...(今度実装して公開できそうなら別途記事にいたします)
森脇 大輔ら,『Kaggleで勝つデータ分析の技術』,技術評論社(2019)(amazon link)のp362を読む限りでは手法IIに似た手法では『学習データについては「目的変数を知っている」予測値になってしまい、テストデータについては「目的変数を知らない」予測値になっているので、学習データとテストデータで意味が違う特徴量となってしま』うため,精度は出ないと紹介されており,p364では,手法Iの実装がされているように思えました.
そのため,先ほど私が指摘した点については,無視できると考えられるのだと思います.というのも,data leakageをある程度許容する手法は様々あり(early stoppingなど)今回の話はそれに含まれてくる話で,精度のためには仕方のないことのように思えるからです.
この辺りの実装や経験値,および私の考えに誤りに考えられそうな部分があれば,コメントお願いいたします🙇♂️
5. 新規デイタへの実装を考える
IIの場合
今までの工程でk*(m+1)個の小さなモデルができました.
そのためミタ・モデルを含めたk個の枠組み(1つあたりm+1のモデルを使用)をとり,
最終的に平均を取ることが一般的であると考えられます:
I の場合
今までの工程で(m+1) x (k)個のモデルができました.
実用的には,それぞれモデルの平均(k個)を取ってから,
m次元の1つの特徴量を作成し,
k個のミタ・モデルを回して平均を取ることが考えられます:
ˈkɑləm 1 : 別の視点の精度保証
ある$x$に対して,モデル1~mまで全てが全くベクトル的にも正反対の結論をしていたら,あまり決定的な結論を採択したくないかもしれません(イラストやから花の画像を引用):
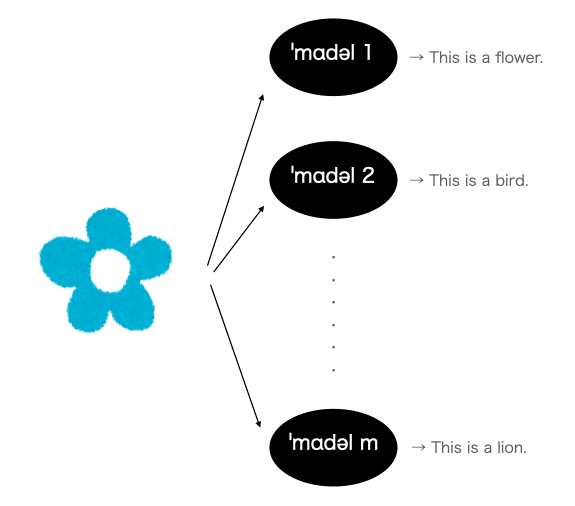
上記の例では,
そもそもモデル一つ一つが明らかに学習不足であると考えられますが,ひとひとつの精度が良いと想定されている場合は非常に難しい課題である可能性があります.
Kaggleなどでは精度を競うためこちらは気にしなくて良いかもしれませんが,学習機を社会実装するとなると,一つの反例が命取りになる場合もあるため,この辺りには,注意していきたいと個人的には感じています.
最後に
記事をご覧いただきありがとうございます!
感想やご指摘があればコメントいただけると幸いです!
LGTMやストックも モチベイションにつながるため,よろしければお願いいたします🙇♂️
参考文献
門脇 大輔, 阪田 隆司, 保坂 桂佑, 平松 雄司『Kaggleで勝つデータ分析の技術』,技術評論社(2019)(amazon link)