書籍「最短コースでわかる PyTorch &深層学習プログラミング」3値分類モデルの決定境界の表示

はじめに

書籍「最短コースでわかる PyTorch &深層学習プログラミング」の著者です。
この本の姉妹版にあたる「最短コースでわかるディープラーニングの数学」の補足として、３値分類モデルの決定境界を求めるコードをアップしたところ、結構評判がいいようなので、調子にのってこちらの本でも同じことをやってみます。

---

書籍のリンクはこちら
2つの書籍は、まったく同じデータを例題で扱っており、こちらの本で３値分類モデルは７章に該当します。

Notebook全体のリンクは、こちらです。

考え方

決定境界とは、２つの確率値が等しくなる点の集まりです。つまり、　softmax関数の入力の時点で考えると、「２つの１次関数の計算結果が等しい場所」ということになります。
これを、重み行列とバイアスの言葉でいいかえると、重み行列とバイアスを当時に一列ずらして元の行列との差をとり、その結果で計算される１次関数の結果がゼロになる場所です。
※　この考え方が成り立つのは正確にいうと例題で扱っている３値分類の場合に限定されます。４値以上の分類の場合は、決定境界の組み合わせがもっと複雑なので、計算もそれに対応して複雑になります。

これから紹介するコードはこの考えに基づいて実装されています。

実装コード紹介

これから紹介する実装コードは、書籍でいうとp.263で学習が終わり、weightとbiasの値の表示までできた後に追加したものです。

x, yの描画領域の計算

決定境界の直線を元の散布図と同時に表示しようとすると。決定境界の直線に引っ張られて、散布図の点と関係ない領域まで表示されてしまいます。そのことを防ぐために、x, yの描画領域をあらかじめ計算し、 axis関数で明示的に描画領域を指定するようにします。
※　この考え方は一般論としては間違っていないのですが、今回の場合は、一番最後の図を見ると、こういう問題は起きなかったみたいです。つまり、結果論としては、y_min, y_maxの計算と、描画のときのaxis関数呼び出しは不要でした。

# x, yの描画領域計算
x_min = x_train[:,0].min()
x_max = x_train[:,0].max()
y_min = x_train[:,1].min()
y_max = x_train[:,1].max()
x_bound = torch.tensor([x_min, x_max])

# 結果確認
print(x_bound)

決定境界のyの値計算用関数

# 決定境界用の１次関数定義

# 決定境界用の１次関数定義
def d_bound(x, i, W, B):
    W1 = W[[2,0,1],:]
    W2 = W - W1
    w = W2[i,:]
    B1 = B[[2,0,1]]
    B2 = B - B1
    b = B2[i]
    v = -1/w[1]*(w[0]*x + b)
    return v

行列W2は上の説明に基づいて実装しています。
その後の計算は、

$ w_0 + w_1 x + w_2 y = 0$

をyについて解いた結果です。

決定境界のｙの値を計算

今、定義した関数を使って、決定境界のyの値を計算していきます。決定境界は全部で３つあります。

# 決定境界のyの値を計算

W = net.l1.weight.data
B = net.l1.bias.data

y0_bound = d_bound(x_bound, 0, W, B)
y1_bound = d_bound(x_bound, 1, W, B)
y2_bound = d_bound(x_bound, 2, W, B)

# 結果確認
print(y0_bound)
print(y1_bound)
print(y2_bound)

tensor([3.0898, 4.9179], dtype=torch.float64)
tensor([2.2871, 3.7670], dtype=torch.float64)
tensor([3.7981, 5.9337], dtype=torch.float64)

グラフ描画

これで準備は全部整いました。あとは、今計算で出したyの値を使ってplot関数で直線を書けばいいだけとなります。

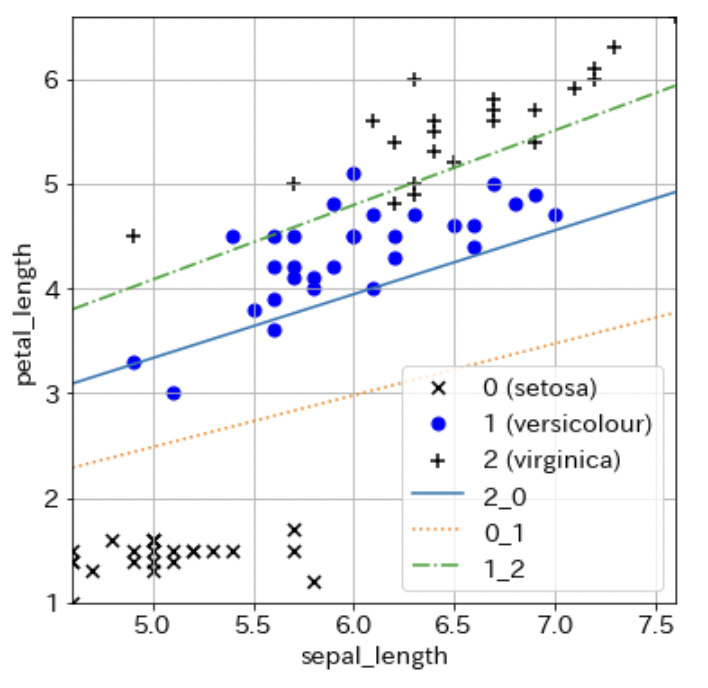
# 散布図と決定境界の標示

# xとyの範囲を明示的に指定
plt.axis([x_min, x_max, y_min, y_max])

# 散布図
plt.scatter(x_t0[:,0], x_t0[:,1], marker='x', c='k', s=50, label='0 (setosa)')
plt.scatter(x_t1[:,0], x_t1[:,1], marker='o', c='b', s=50, label='1 (versicolour)')
plt.scatter(x_t2[:,0], x_t2[:,1], marker='+', c='k', s=50, label='2 (virginica)')

# 決定境界
plt.plot(x_bound, y0_bound, label='2_0')
plt.plot(x_bound, y1_bound, linestyle=':',label='0_1')
plt.plot(x_bound, y2_bound,linestyle='-.',label='1_2')

# 軸ラベルと凡例
plt.xlabel('sepal_length')
plt.ylabel('petal_length')
plt.legend()
plt.show()

下のようなグラフが表示されれば成功です！