はじめに
書籍「Pythonで儲かるAIをつくる」の著者です。
関連リンク:
書籍の4.3節では、2値分類問題を対象に、決定木、サポートベクターマシン、ランダムフォレストなど機械学習の典型的なアルゴリズムをいくつか紹介しています。ここで各アルゴリズムの特徴を説明する手段との一つして、決定境界表示を用いています。
決定境界表示に関しては、現時点で(おそらく?)正式のライブラリがないため、簡易的に表示ができる関数を事前に定義し、書籍の中では、その関数を参照する形にしています。つまり、表示方法そのものに関する解説は一切ありません。この書籍は入門者向けなので、読者はこの実装ロジックを理解する必要はないという判断のもと、こういう方法を取りました。
一方で著者が非常によく聞かれるのが、この関数の中でどうやって決定境界を表示しているかという点です。当記事は、もともとはそのような読者に向けて書くことを意図していたのですが、よく考えると、機械学習をこれから勉強しようとしている人全般にも役立つ情報かと思いました。
そこで「機械学習をこれから勉強しようとしている人全般」を主対象にすることにしました。具体的には、機械学習においてなぜ決定境界表示が重要なのかを説明した上で、代表的なアルゴリズムについて、実際の可視化結果を基にした簡単な説明を加えました。
実装方法解説のパートでは書籍と関係なく、一般的にPythonで自分のつくったモデルの決定境界表示をするにはどうしたらいいか、細かいステップごとに解説を加えました。最後に、まとめの意味で、汎用的に使える決定境界表示関数も紹介しています。読者は、この関数のセルをコピペするだけで自分のつくったモデルに対して、簡単に決定境界表示が可能です。※
実は、この記事を書いている過程で、書籍の決定境界表示関数のイケていないところを何カ所かみつけてしまいました。そこで、書籍「Pythonで儲かるAIをつくる」の読者向けに、知っておくとお得な、書籍の関数を改善する情報を「おまけ」として記載しています。この部分が、元々想定していた読者に向けた特別な情報ということになります。
※ 厳密にいうと、つくったモデルがpredict_proba関数を持っていて、予測値を確率値として取得できることが条件となります。
なぜ「決定境界」なのか
機械学習の中でも教師あり2値分類問題は、説明変数の数をN個とすると、結局のところ学習データに代表されるN次元空間の各点の間にN-1次元の境界面を決める話です。しかし、相手がN次元だと、使える武器が数式しかなく、数学・数式が苦手な人にとって、その瞬間に近づきがたい世界になってしまいます。
これに対して、説明変数を2個に絞れば、出力の確率値を含めて3次元で表現可能なので、ぎりぎり視覚的なイメージで何をやっているか理解可能です。現実のデータ分析の世界で説明変数が2個しかないということはまずありえないのですが、 処理イメージを数式なしで理解する上ではとても強力な道具になるのです。私は、これが**「決定境界」を使う意味**であると考えています。
その具体例を、書籍「 Pythonで儲かるAIをつくる」4.3節の図を使って説明しましょう。
学習データ
これからの説明の中では、下のような学習データを共通に利用します(このデータは「Pythonで儲かるAIをつくる」の中で利用している3つのサンプルデータのうちの1つです)。見てもらえばわかるように、青と黒の2つのデータのグループは明確に分離されていますが、一方で直線では境界をつくることができない、多少意地悪な構造になっています。

ロジスティック回帰の場合
ロジスティック回帰とは、境界線が直線であることを前提としているアルゴリズムです。今回の学習データに対してロジスティック回帰でモデルをつくった場合の決定境界が下図です。

基の入り組んだ学習データに対して対応ができず、不十分な結果になっていることが図から読み取れます。
サポートベクターマシン(rbfカーネル)の場合
scikit-learnのサポートベクターマシンは、何種類かのカーネルアルゴリズムが存在し、インスタンス生成時にオプションで指定可能です。ここでは汎用性の高いrbfカーネルを利用しています。このアルゴリズムを用いた場合の決定境界が、下の図になります。

入り組んだ構造の学習データに対して柔軟に対応できて、人間か手でひくのとほぼ同じ形の自然な形の決定境界ができていることがわかります。
決定木の場合
では、決定木の場合はどのような決定境界になるのでしょうか?それを示したのが、下の図です。

決定木のアルゴリズムとは、「特定の項目値が特定の閾値より大きいか小さいかでグループ分けする」処理の繰り返しです。そのアルゴリズムを説明変数が2次元の場合に翻訳すると、「x軸またはy軸に平行な境界線の組み合わせで決定境界をつくる」ということになります。
上の図の角張った境界線により、そのことをイメージとして理解可能になります。
ランダムフォレストの場合
アルゴリズムをランダムフォレストにした場合の決定境界を下に示します。

ここでは、ランダムフォレストのアルゴリズムを詳しく説明することは省略しますが、概要のみ説明すると「弱分類器と呼ばれる小さな決定木をたくさんつくり、その多数決で分類結果を決定する」という方式です。一つ上の決定木の境界と比較すると、よりなめらかな決定境界になっていますが、一方で、基の決定木アルゴリズムの性質を引き継いで、角張ったところが残っている様子も読み取れます。もう一つ上のサポートベクターマシンほど、きれいな境界にはなっていません。
(参考)LIMEの説明図
2次元の決定境界の便利さを説明するもう一つの事例として、次のリンク先にあるLIMEと呼ばれるアルゴリズムの説明の論文中の図を紹介します。

LIMEというアルゴリズムは、機械学習モデルの局所的な影響度を数値化する手法の一つです。上の図のように入り組んだ決定境界のモデルがあった場合、項目の影響度は全体的な方法では捉えることができず、部分的にどうなっているかを調べるしかありません。LIMEとは、予測対象の入力データの近傍の境界線の傾きの法線ベクトルを影響度と考える手法です。このようなアルゴリズムに関しても、上のように2次元に簡略化した図があると、どんなことをやっているかのイメージが持ちやすくなります。
余談ですが、筆者がIBMでAI関係製品の技術営業をやっていたときには、OpenScaleという製品機能の説明のため、この図にはとてもお世話になりました。
決定境界表示プログラムの大枠
前置きが相当長くなってしまいましたが、いよいよ本題の決定境界表示プログラムの説明に入ります。
決定境界とは、モデルの確率値を入力として描画する場合、「2入力関数の出力値(確率値)の値が0.5である点を結んでつくった等高線」と言い換えることができます。
この等高線を書くことのできる関数は具体的に matplotlibのcontour関数、あるいはcontourf関数です。 これから紹介するサンプルコードも基本的にこの2つの関数を利用して、決定境界表示をしています。(書籍「Pythonで儲かるAIをつくる」で定義した関数も同じです)
この2つの関数で必要なパラメータ(入力データ)は2変数関数の3次元表示用関数とほぼ同じです。そのため、描画用のデータ準備に3次元グラフ表示と同程度の手間がかかります。この点については、これから順を追って説明しますので、まず、今の大枠を頭において説明を読むようにして下さい。
逆に今回のデータ準備ができると、最後に呼び出す関数を差し替えるだけで、2変数関数の3次元表示も簡単にできます。おまけとして、最後にこのグラフ表示もやってみることにします。
実装コード解説
ここから実装コードの解説に入ります。コード全体は、Githubの以下のリンクにアップしておきました。動作確認は2022年2月11日時点のGoogle Colabで行っています。
ライブラリ読み込み・初期設定
最初によく利用するライブラリの導入、インポートや、変数初期設定をまとめて行います。以下の2つのセルが具体的な実装です。
# 日本語化ライブラリ導入
!pip install japanize-matplotlib | tail -n 1
# 共通事前処理
# 余分なワーニングを非表示にする
import warnings
warnings.filterwarnings('ignore')
# 必要ライブラリのimport
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# matplotlib日本語化対応
import japanize_matplotlib
# データフレーム表示用関数
from IPython.display import display
# 表示オプション調整
# グラフのデフォルトフォント指定
plt.rcParams["font.size"] = 14
# 乱数の種
random_seed = 123
サンプルデータ生成
次にscikit-learnのライブラリを利用して、前章で散布図を見せたサンプルデータを生成します。コードは以下の形になります。
# サンプルデータの生成
# ライブラリインポート
from sklearn.datasets import make_moons
# 三日月型 (線形分離不可)
X, y = make_moons(noise = 0.05, random_state=random_seed,
n_samples=200)
# 学習データの最初の列と2番目の列を抽出
X1 = X[:,0]
X2 = X[:,1]
サンプルデータの散布図表示
今、生成したサンプルデータの内容を散布図表示して確認します。実装と結果は次のとおりです。
# カラーマップ定義
from matplotlib.colors import ListedColormap
cmap1 = plt.cm.bwr
cmap2 = ListedColormap(['#0000FF', '#000000'])
# 散布図表示
plt.figure(figsize=(5,4))
plt.scatter(X1, X2, c=y, cmap=cmap2)
plt.show()

モデル生成・学習
rbfカーネルを用いてサポートベクターマシンのインスタンスを生成します。
# モデル生成(アルゴリズム選定)
from sklearn.svm import SVC
algorithm = SVC(kernel='rbf', probability=True, random_state=random_seed)
サポートベクターマシンの場合、普通は確率値を取れませんが、probabilityオプションをTrueにすると、確率値が取れるようになります。確率値は後ほど決定境界グラフ生成で用いるので、このオプションを追加します。random_stateオプションを指定しているのは、結果をいつも同じにするためです。
更に先ほど用意したサンプルデータを使って学習します。
# 学習
algorithm.fit(X, y)
今回は、決定境界描画が目的なので、コードを簡略化するため、訓練データと検証データへの分割は行わず、全データを使って学習します。
グラフ描画用メッシュ生成
ここからが、決定境界描画で固有の実装になります。まず、グラフ描画用のメッシュを生成します。
メッシュ(格子点)のイメージを下の図に示しました。
x軸とy軸の値を示すNumPyの1次元配列2つを引数として、図のような2次元の格子状の配列f1とf2を得ることを目的とする関数が、np.meshgrid 関数です。具体的な実装は、以下になります。
# グラフ描画用メッシュ生成
# メッシュの刻み幅
h = 0.005
# それぞれの最小値と最大値を計算
f1_min, f1_max = X1.min(), X1.max()
f2_min, f2_max = X2.min(), X2.max()
# 最小値と最大値の間を刻み幅で等間隔に区切る
f1_range = np.arange(f1_min, f1_max+h, h)
f2_range = np.arange(f2_min, f2_max+h, h)
# 上の結果を基にメッシュ配列の生成
f1, f2 = np.meshgrid(f1_range, f2_range)
# 結果の一部確認
print(f1[0,:5])
print(f2[0,:5])
最後のprint関数の結果は以下の通りです。
[-1.14500246 -1.14000246 -1.13500246 -1.13000246 -1.12500246]
[-0.6067159 -0.6067159 -0.6067159 -0.6067159 -0.6067159]
上の図と見比べて、なぜこの値になっているか確認して下さい。
モデル入力用変数生成
次に、上の格子点のそれぞれの値での、予測値(確率値)を得るため、格子点データをモデル入力データの形に変換します。
そのため、f1とf2それぞれをravel関数で1次元化した後、np._cを使って横連結します。
実装は以下の形です。
# モデル入力用変数生成
# f1, f2からN行2列のNumPy配列を生成する
w = np.c_[f1.ravel(), f2.ravel()]
print(w.shape)
print(w[:,:10])
最後のprint関数の出力は、以下のようになります。
(212424, 2)
[[-1.14500246 -0.6067159 ]
[-1.14000246 -0.6067159 ]
[-1.13500246 -0.6067159 ]
...
[ 2.01999754 1.0582841 ]
[ 2.02499754 1.0582841 ]
[ 2.02999754 1.0582841 ]]
予測(確率値取得)
最後につくった変数wを用いて、モデルの予測値(正確にいうと、予測値1に対応する確率値)を取得します。取得した予測値は、f1, f2と同じ2次元格子状の形状に戻します。具体的な実装は以下の通りです。
# 予測(確率値取得)
# (予測値0に対する確率値は捨てる)
Z = algorithm.predict_proba(w)[:,1]
# 結果を2次元メッシュ状に戻す
W = Z.reshape(f1.shape)
# 各変数のshape確認
print(Z.shape)
print(W.shape)
print(f1.shape)
print関数の出力は以下のとおりで、予測値を得るため、いったんZが一次元の形状だったのが、Wでは、f1と同じ2次元の形状になっていることがわかります。
(212424,)
(334, 636)
(334, 636)
お疲れ様でした。最初に生成した f1とf2、更に最後につくったW(格子点に対応する確率値の配列)があれば、これらを引数にいろいろなグラフを描画可能です。その点をこれから順に確認していきます。
contourf関数を用いて等高線表示
よく山の地図などで、2つの等高線に囲まれた高さの同じ領域を同じ色で塗りつぶした図を見ます。contourf関数は、これと同じ考え方で、塗りつぶしを行う関数です。基の学習データの散布図と、この塗りつぶし結果を重ねがきするコードが下記になります。
# contourf関数を用いて等高線表示
plt.figure(figsize=(5,4))
plt.scatter(X1, X2, c=y, cmap=cmap2)
plt.contourf(f1, f2, W, cmap=cmap1, alpha=0.3)
plt.show()
このコードの結果は以下のとおりです。

contour関数を用いて決定境界表示
contourf関数が、等高線に囲まれた領域の塗りつぶしだったのに対して、これから紹介するcontour関数は等高線そのものを表示します。確率値のグラフの場合、関数値=0.5に対応する等高線が、今、求めたい決定境界です。まずは、学習データの散布図と、決定境界を同時に表示してみます。実装は、下記の形になります。
# contour関数を用いて決定境界表示
# 確率値で見たとき、決定境界とは確率値が0.5の点をつないだ曲線
plt.figure(figsize=(5,4))
plt.scatter(X1, X2, c=y, cmap=cmap2)
plt.contour(f1, f2, W, levels=[0.5], linewidth=2)
plt.show()
結果のグラフは以下のようになります。

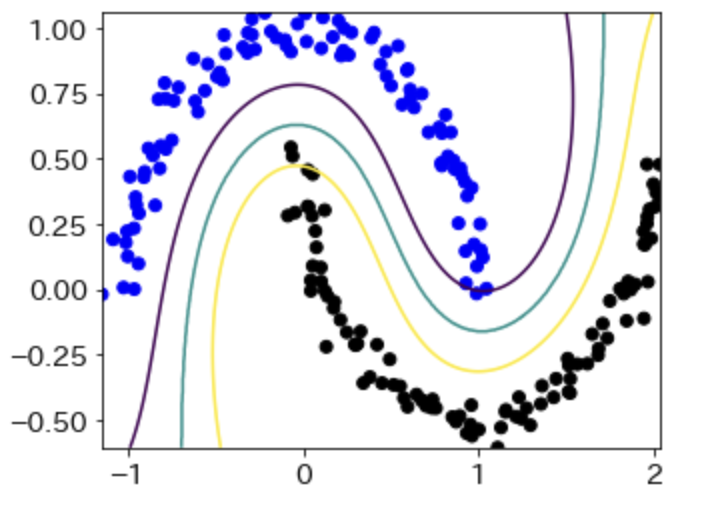
contour関数を用いて複数の境界表示
contour関数では、複数の等高線を同時に表示することもできます。次の実装では、0.1, 0.5, 0.9それぞれの確率値に対する等高線を表示しました。今回は、結果もセットで示します。
# contour関数を用いて複数の境界表示
# 等高線の値を複数与えることも可能
plt.figure(figsize=(5,4))
plt.scatter(X1, X2, c=y, cmap=cmap2)
plt.contour(f1, f2, W, levels=[0.1,0.5,0.9], linewidth=2)
plt.show()
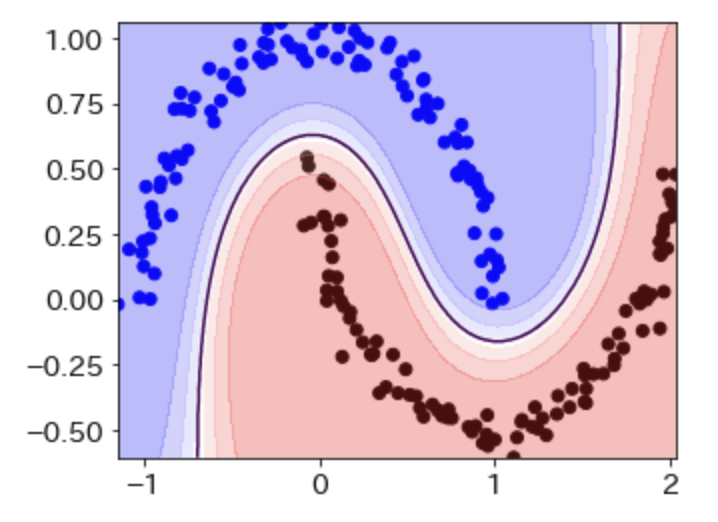
contourf関数とcontour関数を同時に利用
最後に2つの関数を重ねかきしてみましょう。この結果が、「Pythonで儲かるAIをつくる」の図と同じものになります。今回もコードと結果を同時に示します。
# contourf関数とcontour関数を同時に利用
plt.figure(figsize=(5,4))
plt.scatter(X1, X2, c=y, cmap=cmap2)
plt.contourf(f1, f2, W, cmap=cmap1, alpha=0.3)
plt.contour(f1, f2, W, levels=[0.5], linewidth=2)
plt.show()
確率値を3次元曲面表示
これはおまけです。今まで決定境界表示に使ったデータ(f1, f2, W)を、別の関数plot_surfaceにかけると、関数グラフ曲面の3次元表示が可能です。コードと結果を以下に示します。
# 確率値を3次元曲面表示
from mpl_toolkits.mplot3d import Axes3D
plt.figure(figsize=(8,8))
ax = plt.subplot(1, 1, 1, projection='3d')
ax.plot_surface(f1, f2, W, color='blue',
rstride=10, cstride=10, alpha=0.2)
plt.show()

決定境界表示関数
前章では、処理の一つ一つをわかりやすくするため、ステップを細かく刻みましたが、普段使うときは、関数として一つにまとまっていた方が便利です。
その実装例を以下に示します。
関数定義
まずは、関数定義側です。
# 決定境界表示関数
def show_boundary(X, y, algorithm, h=0.005):
X1 = X[:,0]
X2 = X[:,1]
f1_min, f1_max = X1.min(), X1.max()
f2_min, f2_max = X2.min(), X2.max()
f1_range = np.arange(f1_min, f1_max+h, h)
f2_range = np.arange(f2_min, f2_max+h, h)
f1, f2 = np.meshgrid(f1_range, f2_range)
w = np.c_[f1.ravel(), f2.ravel()]
Z = algorithm.predict_proba(w)[:,1]
W = Z.reshape(f1.shape)
# グラフ描画
from matplotlib.colors import ListedColormap
cmap1 = plt.cm.bwr
cmap2 = ListedColormap(['#0000FF', '#000000'])
plt.figure(figsize=(5,4))
plt.scatter(X1, X2, c=y, cmap=cmap2)
plt.contourf(f1, f2, W, cmap=cmap1, alpha=0.3)
plt.contour(f1, f2, W, levels=[0.5], linewidth=2)
plt.show()
利用サンプル
次にこの関数の利用例を示します。この関数は、学習用データ(X)、対応する正解データ(y)、学習済みモデルの3つを引数で取ります。
以下の実装は、この3つの準備をコンパクトにまとめたものです。
前提コード
# サンプルデータの生成
# ライブラリインポート
from sklearn.datasets import make_moons
# 三日月型 (線形分離不可)
X, y = make_moons(noise = 0.05, random_state=random_seed,
n_samples=200)
# モデル生成(アルゴリズム選定)
from sklearn.svm import SVC
algorithm = SVC(kernel='rbf', probability=True, random_state=random_seed)
# 学習
algorithm.fit(X, y)
呼び出し例1(デフォルトの刻み値)
これで関数を呼び出す準備ができました。格子点の刻み幅を意味するパラメータhは指定してもしなくてもよく、しない場合はデフォルト値0.005が用いられます。まずは、この条件で呼び出す場合の実装と結果を示します。
show_boundary(X, y, algorithm)

呼び出し例2(刻み値の変更)
次に違いを確認するため、わざと荒い刻み値である 0.5をパラメータに指定して、同じ関数を呼び出してみます。実装と結果は次のようになります。
show_boundary(X, y, algorithm, h=0.5)

境界線のカーブが荒くなったのがわかります。
書籍「Pythonで儲かるAIをつくる」修正コード
簡易修正版(どの場合も決定境界が標示される)
書籍の決定境界表示関数は、決定関数(decision_function)を持つものは、そちらを呼び出す作りです。決定関数を持っていない場合は、確率値を使っているのですが、「確率値0.5を使った等高線表示」をしていないため、このようなケースでは等高線表示がない形になっています。1行追加しただけなのですが、以下の実装に切り替えると、どのようなアルゴリズムであっても、決定境界表示がされるようになります。
# 簡易修正版(どの場合も決定境界が標示される)
from sklearn.model_selection import train_test_split
# 決定境界の表示関数
def plot_boundary(ax, x, y, algorithm):
x_train, x_test, y_train, y_test = train_test_split(x, y,
test_size=0.5, random_state=random_seed)
# カラーマップ定義
from matplotlib.colors import ListedColormap
cmap1 = plt.cm.bwr
cmap2 = ListedColormap(['#0000FF', '#000000'])
h = 0.005
algorithm.fit(x_train, y_train)
score_test = algorithm.score(x_test, y_test)
score_train = algorithm.score(x_train, y_train)
f1_min = x[:, 0].min() - 0.5
f1_max = x[:, 0].max() + 0.5
f2_min = x[:, 1].min() - 0.5
f2_max = x[:, 1].max() + 0.5
f1, f2 = np.meshgrid(np.arange(f1_min, f1_max, h),
np.arange(f2_min, f2_max, h))
if hasattr(algorithm, "decision_function"):
Z = algorithm.decision_function(np.c_[f1.ravel(), f2.ravel()])
Z = Z.reshape(f1.shape)
ax.contour(f1, f2, Z, levels=[0], linewidth=2)
else:
Z = algorithm.predict_proba(np.c_[f1.ravel(), f2.ravel()])[:, 1]
Z = Z.reshape(f1.shape)
# この下の行を追加
ax.contour(f1, f2, Z, levels=[0.5], linewidth=2)
ax.contourf(f1, f2, Z, cmap=cmap1, alpha=0.3)
ax.scatter(x_test[:,0], x_test[:,1], c=y_test, cmap=cmap2)
ax.scatter(x_train[:,0], x_train[:,1], c=y_train, cmap=cmap2, marker='x')
text = f'検証:{score_test:.2f} 訓練: {score_train:.2f}'
ax.text(f1.max() - 0.3, f2.min() + 0.3, text, horizontalalignment='right',
fontsize=18)
抜本修正版(どのケースもpredict_proba関数を使うことで実装をシンプルに)
そもそも書籍の5.3節で取り上げているアルゴリズムの場合、すべて確率値でいけそうです。(上で説明したとおり、唯一怪しいサポートベクターマシンは、オプションを付ければ対応可能)。その場合、関数の実装自体、次のようなもっとシンプルにすることができます。
# 抜本修正版
# predict_proba関数のみ使うように」して実装をシンプルに
# メッシュ計算のロジックもきれいに修正
# 精度はタイトルで表示するように修正
from sklearn.model_selection import train_test_split
# 決定境界の表示関数
def plot_boundary(ax, x, y, algorithm):
x_train, x_test, y_train, y_test = train_test_split(x, y,
test_size=0.5, random_state=random_seed)
# カラーマップ定義
from matplotlib.colors import ListedColormap
cmap1 = plt.cm.bwr
cmap2 = ListedColormap(['#0000FF', '#000000'])
h = 0.005
algorithm.fit(x_train, y_train)
score_test = algorithm.score(x_test, y_test)
score_train = algorithm.score(x_train, y_train)
x1, x2 = x[:,0], x[:,1]
f1_min, f1_max = x1.min(), x1.max()
f2_min, f2_max = x2.min(), x2.max()
f1, f2 = np.meshgrid(np.arange(f1_min, f1_max+h, h),
np.arange(f2_min, f2_max+h, h))
Z = algorithm.predict_proba(np.c_[f1.ravel(), f2.ravel()])[:,1]
Z = Z.reshape(f1.shape)
ax.contour(f1, f2, Z, levels=[0.5], linewidth=2)
ax.contourf(f1, f2, Z, cmap=cmap1, alpha=0.3)
ax.scatter(x_test[:,0], x_test[:,1], c=y_test, cmap=cmap2)
ax.scatter(x_train[:,0], x_train[:,1], c=y_train, cmap=cmap2, marker='x')
text = f'検証:{score_test:.2f} 訓練: {score_train:.2f}'
ax.set_title(text)
ついでに精度の表示場所も、見やすいようタイトルの場所に移しておきました。この関数に置き換えると、こんな感じのグラフになります。

おわりに
当記事で説明した内容は、後半の決定境界実装の解説を除いて、冒頭で説明した書籍「Pythonで儲かるAIをつくる」の内容のごく一部になります。より、機械学習モデルについて詳しく知りたい場合は、是非、書籍もお買い求めいただければ幸いです。
