Introduction
個別要素法(DEM)は陽解法の粒子シミュレーション手法で、各時間ステップごとに時間刻み幅$\Delta t$に速度vをかけた距離だけ粒子を移動させる。
$\Delta t$が大きければ1 time step当たりの移動距離は大きくなる。
個別要素法では粒子同士の重なりが生じた場合にそれを押し返す力を発生させることで接触力を模擬しており、大きな重なりは通常大きな反発力として表現される。
そのため、1回の移動で大きな距離を動かすと粒子同士の意図しない大きな重なりを生じさせ、そこから発生させる大きな反発力が異常な力として計算に問題を生じさせることがありえる。
しかし細かな時間刻みは計算回数を増大させるので、危険のない範囲である程度大きな刻みで計算を行いたいが、適切な刻み幅が事前に予見できているとは限らない。
また、行う計算によっては計算中のある時間範囲では粒子が激しく動き細かな時間刻みが必要なものの、別の時間範囲では粒子の動きが少なく大きな時間刻みでも十分なこともある。
そこで我々のDEMシミュレーションプログラムには、leap-frog法時間発展の途中で時間刻み幅を増大あるいは縮小させながら計算を続ける機能を持たせている。
今回はこのシミュレーションプログラムのサンプル計算から、この時間刻み幅調節のパラメータ推定法を考察する。
実験に用いたサンプル計算の動画は
https://www.youtube.com/watch?v=VRGn9jtGgs8
で公開している。
23408粒子からなる系である。
Background
最大の速度を保つ粒子の速度を$v^*$として、時間刻み幅$\Delta t$で進む距離が何らかの閾値を上回ったら危険性を予知して$\Delta t$を小さく切り下げる。逆に$v^* \Delta t$が別の閾値を下回ったら、十分な安全性を仮定して$\Delta t$を大きく切り上げる操作を考える。
つまり、二つの判定は
v^* \Delta t \geq L_1 \\
v^* \Delta t \leq L_2
で、系の基準長さをなにか考えたとして、それをLとおけば
v^* \geq L / \Delta t \times p_1\\
v^* \leq L / \Delta t \times p_2
であり、
v^* / (L / \Delta t) \geq p_1\\
v^* / (L / \Delta t) \leq p_2
と考えれば、系の基準長さと時間刻みから得られる速度に対する最速粒子の速度の比が、計算パラメータ2つで抑えられていれば良いとわかる。
我々のDEM計算プログラムではこの速度比を元にした$\Delta t$の制御を行っており、まずはこの上限・下限について確認する。
なお基準長についてはDEM粒子の直径を用い、閾値は$p_1 = 0.01\times n$ ($n=1,2,3,4,5$)あるいは$p_2 = 0.01/n$ ($n=16,12,10,8,4$)を用いた。
Results
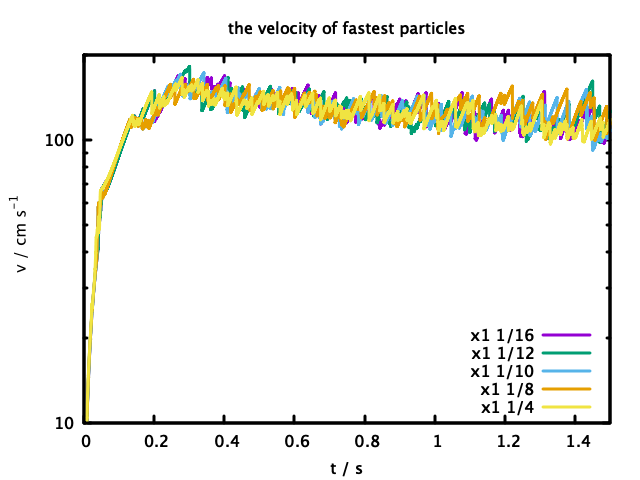
同一のサンプル計算を異なる時間刻み幅調節パラメータで行った際の、最速粒子の粒子速度の推移を図1に示す。以下の図では縦軸は全てlog scaleである。
初速0の分布から初めて、シミュレーション時刻0.2s付近で100cm/s程度になり、その後は大きな変化はなかったことがわかる。
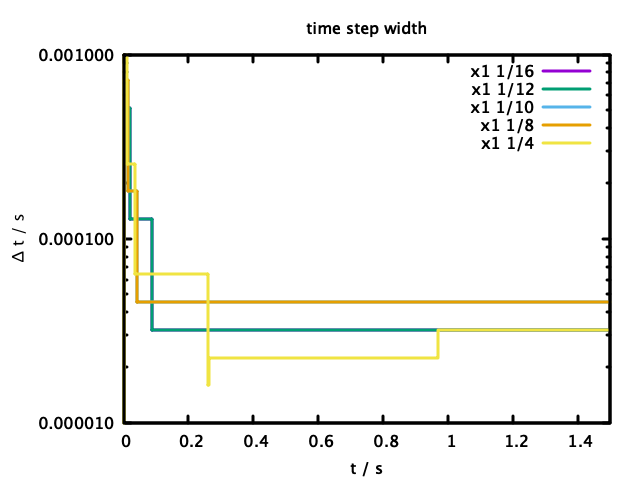
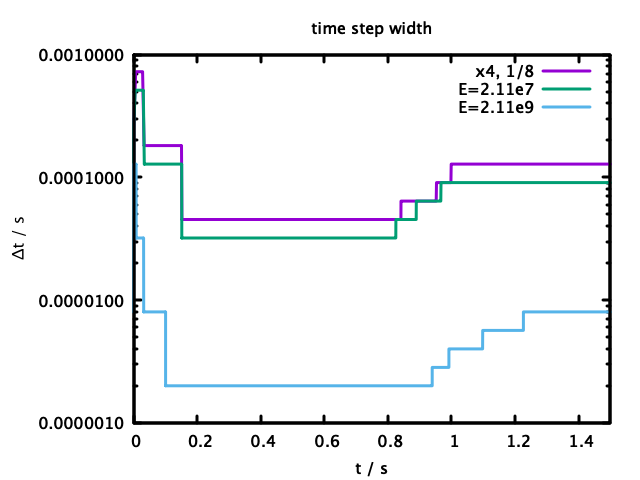
この時の、各パラメータでの計算の、時間刻み幅の推移を図2に、前述の速度比の推移を図3に示す。$\Delta t$は初期値0.000008で始めており、切り上げ操作では$\sqrt 2$倍、切り下げ操作では0.25倍で変化させている。
図2からは、開始直後に$\Delta t$を初期値から増大させたのち、改めて必要な細かさまで縮小させている動作が見て取れる。特に、"x1 1/4"と示されたものでは、時刻0.3付近で0.00002以下まで切り下げたのちに0.00002より大きな値に戻し、さらに時刻1付近でさらに0.00003程度にまた戻している。
この時の、各計算の計算step数と計算時間は表1のようになっていた。
大きな時間刻み幅で計算を終えられた"x1 1/10"と"x1 1/8"が計算step数と計算時間で有利だったことがわかる。
表1 計算step数と計算時間
| x1 1/16 | x1 1/12 | x1 1/10 | x1 1/8 | x1 1/4 | |
|---|---|---|---|---|---|
| 計算step数 | 44733 | 44733 | 32418 | 32418 | 51551 |
| 計算時間/s | 132 | 139 | 103 | 105 | 162 |
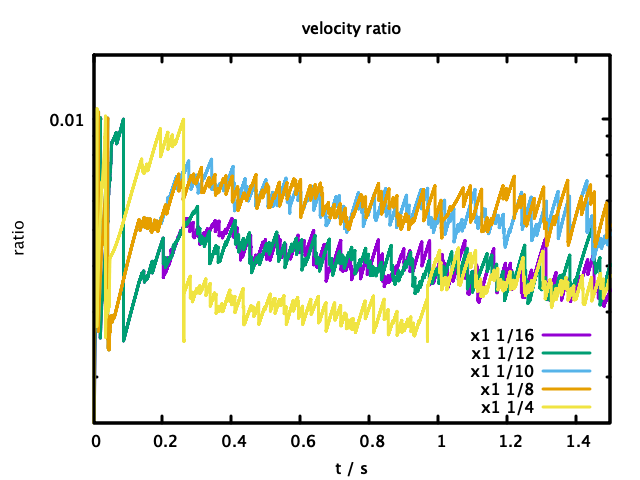
図3 DEM計算中の最速粒子の速度の基準速度に対する比の推移1
図3の速度比の推移を詳細に検討すると、安全とみなして時間刻み幅を大きく切り上げるパラメータp2を貪欲に大きめにとった"x1 1/4"では時刻0.2付近までは大きな速度比(大きな$\Delta t$)で計算を進めたものの、その後上限側の閾値を超えて他のパラメータとの時よりも小さな速度比(小さな$\Delta t$)での計算を余儀なくされていたことが分かる。時刻1.0付近で、"1/16"などと同程度に復帰しているものの、この間の細かな時間刻みでの計算のために計算step数では一番多くなり一番計算時間がかかっていた。
図3に示した計算では、速度比に対する上限パラメータp1は0.01x1であり、これを上回った時に$\Delta t$を0.25倍して範囲内への抑え込みを行っている。
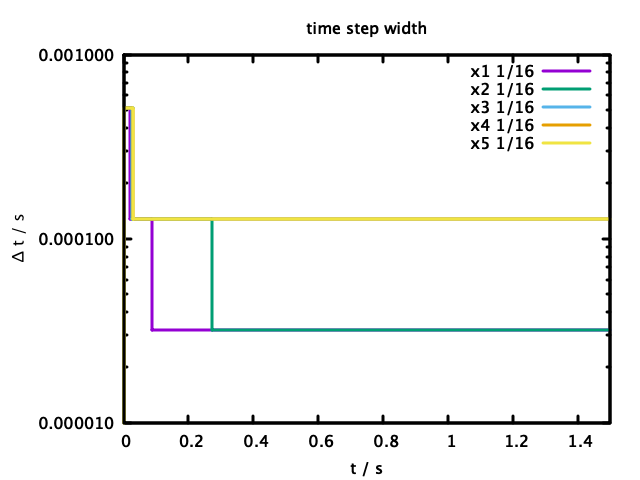
一方、図4、図5では上限側パラメータp1を$0.01\times n (n=1,2,3,4,5)$と変化させた時の、基準速度に対する速度比と$\Delta t$の推移を示している。
”x1”、”x2”の紫と緑の線は、速度比がそれぞれ0.01、0.02にぶつかったところで下に切り下げられており、ここで\Delta tの調節が起こったことが見て取れる。
この計算では、0.03以上にまでこの速度比が上昇することがなかったため"x3"以上のパラメータでは同じ計算結果を与えている。"x1", "x2"ではより小さな$\Delta t$で、同じトラジェクトリを辿り、"x3", "x4", "x5"より計算時間で不利であったことが分かる。
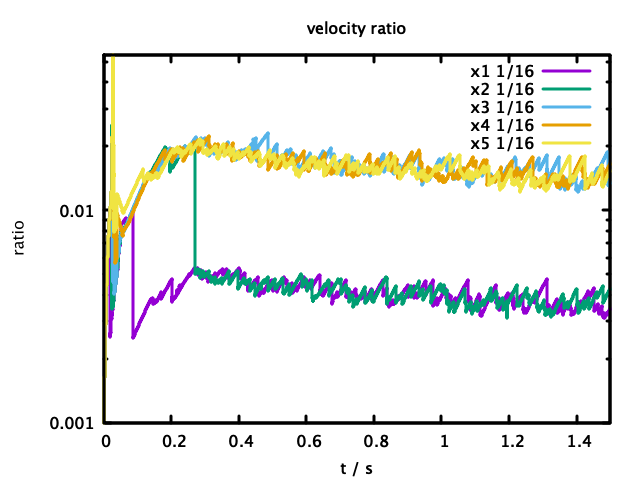
図4 DEM計算中の最速粒子の速度の基準速度に対する比の推移2
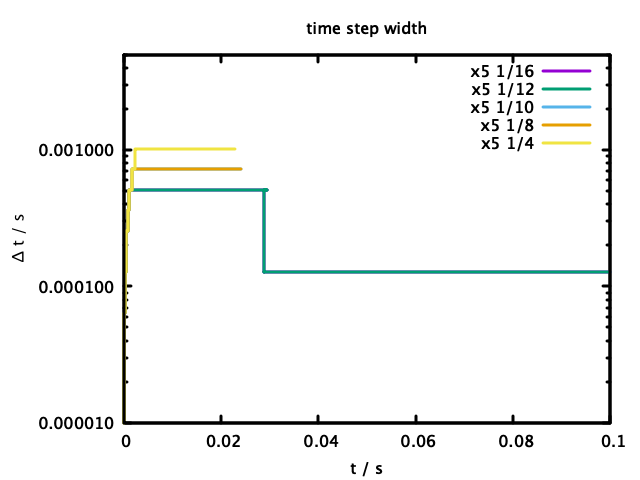
次に、上限側のパラメータが"x5"の場合の下限側のパラメータの効果を確認する。
図6が上限側のパラメータが"x5"の場合の最速粒子の速度の基準速度に対する比の推移で、このケースでは、下限側パラメータ"1/10", "1/8", "1/4"が開始してすぐ($t\sim 0.02$)異常終了している。
開始直後の上昇カーブが3種類見えているが、図7の$\Delta t$の推移で確認するとそれぞれ異なる時間刻みで時間発展させていたことがわかる。そのうち、異常終了しなかった"1/12", "1/16"のものが一番小さく、下限側パラメータがこの範囲では時間刻み幅を大きくするために効果を持っていたが、一方で上限側パラメータが大きすぎて効果を持たなかったために異常終了を回避できなかったと考えられる。
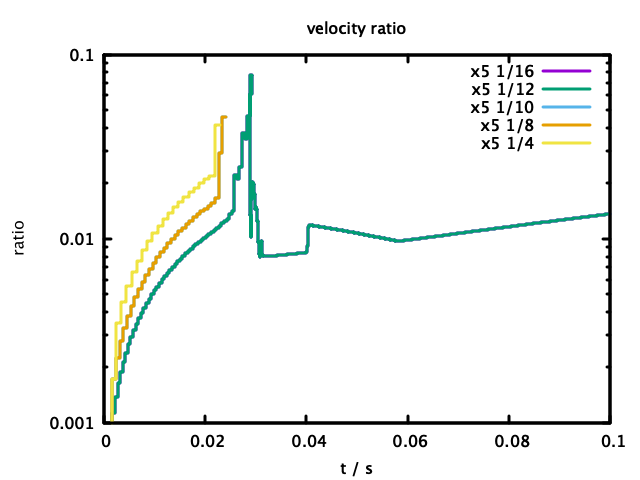
図6 DEM計算中の最速粒子の速度の基準速度に対する比の推移3
表2に時間刻み幅を調節する2種のパラメータの組み合わせと計算step数をまとめた。
今回の計算で計算step数が一番少なく計算時間的に一番有利だったのは、上限側パラメータが"x4"で下限側パラメータが"1/10", "1/8"のものだった。この時、"x1 1/16"のパラメータセットで計算した時と比べて0.18倍の計算step数であり、パラメータ設定が適切であれば、必要に応じて大きな粗さで計算することで計算時間を十分短縮できることがわかった。
表2 時間刻み幅を調節する2種のパラメータの組み合わせと計算step数
| 1/16 | 1/12 | 1/10 | 1/8 | 1/4 | |
|---|---|---|---|---|---|
| x1 | 44733 | 44733 | 32418 | 32418 | 51551 |
| x2 | 40380 | 41142 | 30888 | 30888 | 22243 |
| x3 | 11570 | 11570 | 29274 | 29274 | 21682 |
| x4 | 11564 | 11564 | 8201 | 8201 | 21034 |
| x5 | 11561 | 11561 | abort | abort | abort |
同様のベンチマーク計算を https://www.youtube.com/watch?v=QVuR-hGieh0 についても行った。こちらは27894粒子系である。
確認したパラメータは上限側"x1", "x2", "x4"、下限側"1/16", "1/12", "1/8"の組み合わせで、
要した計算回数を以下の表3にまとめた。
表3 時間刻み幅を調節する2種のパラメータの組み合わせと計算step数
| 1/16 | 1/12 | 1/8 | |
|---|---|---|---|
| x1 | 101274 | 103987 | 68218 |
| x2 | 35512 | 33575 | 24186 |
| x4 | 31196 | 29732 | 22111 |
また、"x1 1/16", "x2 1/12", "x4 1/8"の3例について、基準速度に対する速度比と時間刻み幅の推移を図8に乗せた。この計算では計算開始直後に時間刻み幅を切り上げたのち、$t\sim 0.2$あたりまでで再度細かな時間刻みに戻している。
その後、$t\sim 0.8$付近で粒子の動きが少なくなったために、また$\Delta t$を大きく戻している。
これらの時間刻みの調節は傾向としてはどのパラメータでも同じ流れに従っているが、結果としては22111回と101274回で、最大4.5倍の計算step数を要していた。
これは適正な調節パラメータのもとでは、1/4.5の計算コストで済ませられることを意味し、この上下限パラメータの設定が重要なことがわかる。
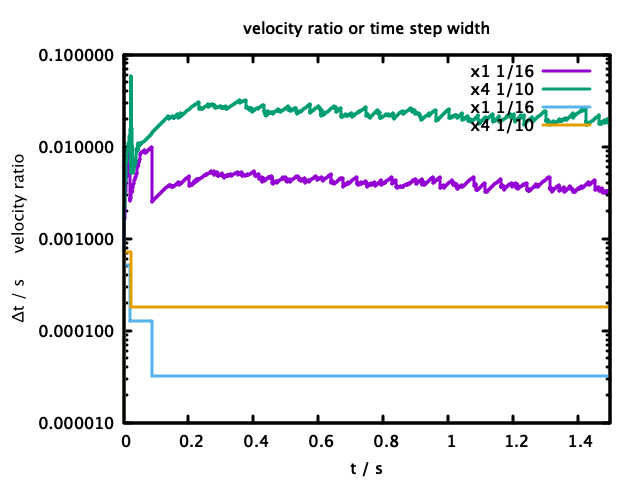
図8 DEM計算中の基準速度に対する速度比と時間刻み幅の推移
Consideration
我々のDEM計算は法線力を線形弾性と粘性を並列に配置した線形ケルビンモデルで模擬していた。
この弾性項で許容する歪み・応力をどう評価していたのか考えてみる。
線形ケルビンモデルによる法線力を以下で計算していた。
F^n = K_n \delta _n
- 2\gamma \sqrt{\langle m \rangle K_n} \dot{\delta _n} \\
ここで
K_n \delta _n
= \frac{2}{3} \frac{E}{1-\nu ^2} \sqrt{\frac{r_i r_j}{r_i + r_j}}\delta ^{3/2}
で、$\delta$は粒子の重なりなので$2r\alpha$、$r_i=r_j$として、
= \frac{2}{3} \frac{E}{1-\nu ^2} \sqrt{\frac{r}{2}}(2r\alpha)^{3/2} \\
= \frac{4}{3} \frac{E}{1-\nu ^2} r^2 \alpha^{3/2}.
$E, \nu$はYoung率とPoisson比である。
$\langle m \rangle = m_i m_j /(m_i + m_j)$で$m_i=m_j$として$=m/2$
\sqrt{\langle m \rangle K_n} = \sqrt{\frac{m}{2} \frac{2}{3} \frac{E}{1-\nu ^2}\sqrt{\frac{r}{2}}(2r\alpha)^{1/2}} \\
=\sqrt{\frac{m}{3}\frac{E}{1-\nu ^2}r\alpha^{1/2}}
=\sqrt{\frac{m}{3}\frac{E}{1-\nu ^2}r\alpha^{1/2}}
そして$\dot{\delta _n}$を最悪ケースで許容速度$\bar{v} = 2r \alpha / \Delta t$と考えれば、
a = F^n / m = \frac{4}{3} \frac{E}{1-\nu ^2} r^2 \alpha^{3/2} / m
- 2\gamma \sqrt{\frac{m}{3}\frac{E}{1-\nu ^2}r\alpha^{1/2} }
\bar{v} / m \\
= \frac{4}{3m}\frac{E}{1-\nu ^2}r^2 \alpha^{3/2} -
2\gamma \sqrt{\frac{1}{3m}\frac{E}{1-\nu ^2} r\alpha^{1/2}} (2r\alpha / \Delta t) \\
= \frac{4}{3m}\frac{E}{1-\nu ^2}r^2 \alpha^{3/2} -
2\gamma \sqrt{\frac{4}{3m}\frac{E}{1-\nu ^2}r^2\alpha^{3/2}} \frac{\sqrt{r\alpha}}{\Delta t} .\\
$\gamma $はdumping factor で、反発係数$e$から$e=0.85$程度として$2\gamma \cong 0.1$と与えていた。
前節のベンチマーク計算では、シミュレーションパラメータは$E=2.11\times 10^7$, $\nu=0.29$, $r=0.5$、$\rho =7.874$としており
\frac{4}{3m}\frac{E}{1-\nu ^2}r^2 =
\frac{4}{3 \times 4.12} \frac{2.11\times 10^{7}}{1-0.0841}\times 0.5^2 \\
= \frac{2.11\times 10^{7}}{11.320524}
= 1.864 \times 10^6
反発項だけ評価して、$1.864\times 10^6 \alpha ^{3/2}$が、シミュレーション計算中でそれ以外で設定している加速度$g=980$とオーダーで合わせることを考えれば、$\alpha$は0.006程度。
Conculusion
今回のケースでは$\frac{4}{3m}\frac{E}{1-\nu ^2}r^2 \alpha^{3/2}$が他の加速度と同程度という要請で求めた$\alpha$は0.006程度で、
実際にパラメータ探索で得られた上限側パラメータ"x4"とは5倍程度の開きがあった。
指標として、5倍程度に抑える$\alpha$というのが安全パラメータとしてありえると考えられる。
下限側パラメータは、"x4"$\sim$ "1/8"のように$2^5$幅ぐらいを与えていればよさそうだった。
確認のために、上限側パラメータ$\alpha $を計算で求めるコードで、$E=2.11\times 10^7, \times 10^9$の2通りの計算を行なったがどちらも異常終了させることなく完走した。
個別要素法で時間刻みを可変型にし、そのための制御パラメータもシミュレーション物性値から決定することで計算ステップ数を適切に圧縮でき計算時間を短縮することが可能となった。
| E | $\alpha$ | steps | times/s |
|---|---|---|---|
| $2.11\times 10^7$ | 0.028082 | 30567 | 132 |
| $2.11\times 10^9$ | 0.0013035 | 530735 | 1774 |