はじめに
拙作の記事「株価の指標を求める」では、TA-Libを使用していろいろな指標を求めてみました。本記事ではこの中のSMA(単純移動平均)を使って、ゴールデンクロスとデッドクロスを求めてみます。そしてゴールデンクロスとデッドクロス後に株価がどのように変化しているか、また短期と長期で最も変化率が大きい組み合わせは何かを調べていきたいと思います。
ゴールデンクロス/デッドクロスを求める
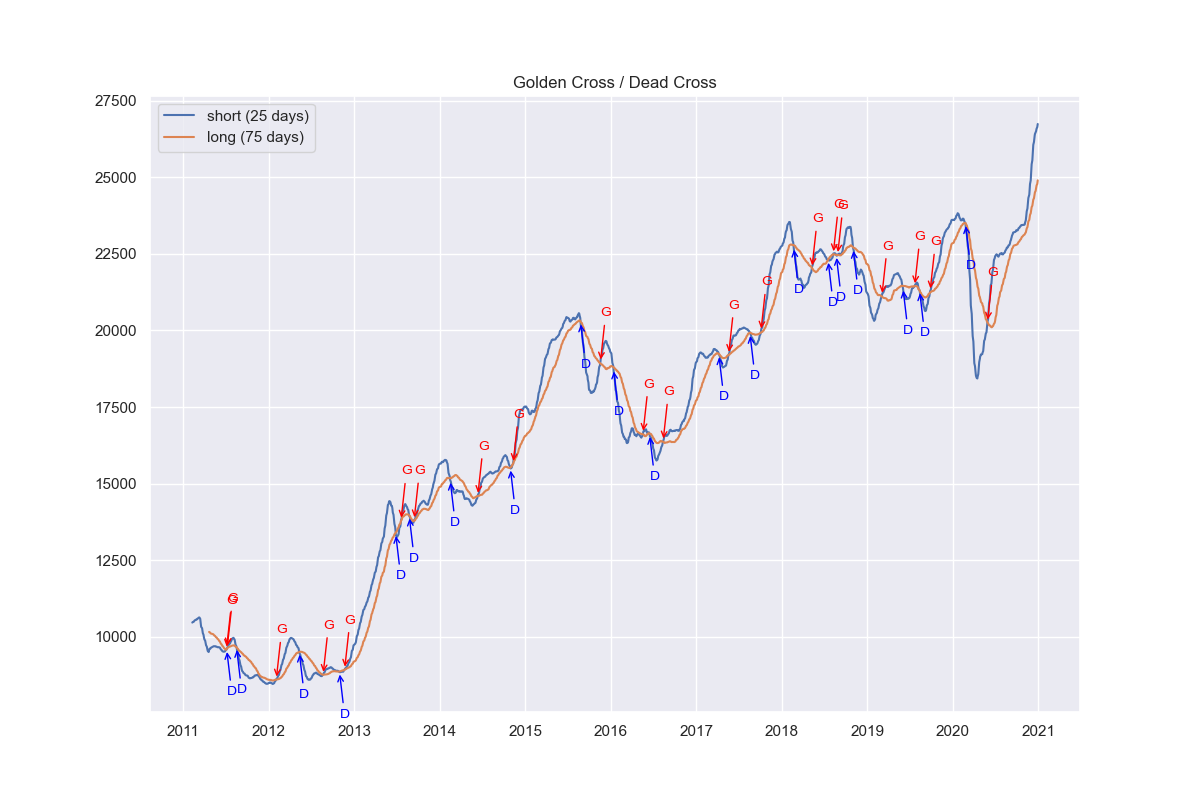
今回使用するデータは日経平均株価で、期間は2011/1/1〜2020/12/31の10年間としています。まずは短期線と長期線を求めます。短期線は25日、長期線は75日としました。計算はTA-Libで行っています。ゴールデンクロス/デッドクロスが正しく求められているかグラフも作成してみました。
import os
import datetime
import pandas as pd
import pandas_datareader
import talib
import matplotlib.pyplot as plt
import seaborn as sns
START_DATE = datetime.date(2011, 1, 1)
END_DATE = datetime.date(2020, 12, 31)
def get_stock(ticker, start_date, end_date):
'''
get stock data from Yahoo Finance
'''
dirname = 'data'
os.makedirs(dirname, exist_ok=True)
fname = f'{dirname}/{ticker}.pkl'
df_stock = pd.DataFrame()
if os.path.exists(fname):
df_stock = pd.read_pickle(fname)
start_date = df_stock.index.max() + datetime.timedelta(days=1)
if end_date > start_date:
df = pandas_datareader.data.DataReader(
ticker, 'yahoo', start_date, end_date)
df_stock = pd.concat([df_stock, df[~df.index.isin(df_stock.index)]])
df_stock.to_pickle(fname)
return df_stock
def main():
short_term = 25
long_term = 75
df = get_stock('^N225', START_DATE, END_DATE)
# 移動平均を求める
df['short_ma'] = talib.SMA(df['Close'], timeperiod=short_term)
df['long_ma'] = talib.SMA(df['Close'], timeperiod=long_term)
# クロスしている箇所を見つける
df['diff'] = df['long_ma'] - df['short_ma']
df_cross = df[df['diff'] * df['diff'].shift() < 0]
df['golden_cross'] = df.index.isin(df_cross[df_cross['diff'] < 0].index)
df['dead_cross'] = df.index.isin(df_cross[df_cross['diff'] > 0].index)
# グラフで表示する
sns.set()
fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(df['short_ma'], label=f'short ({short_term} days)')
ax.plot(df['long_ma'], label=f'long ({long_term} days)')
ax.set_title('Golden Cross / Dead Cross')
ax.legend()
for index, row in df[df['golden_cross']].iterrows():
ax.annotate('G', xy=(index, row['short_ma']),
xytext=(index, row['short_ma'] + 1500),
size=10, color='red',
arrowprops={'arrowstyle': '->', 'color': 'red'})
for index, row in df[df['dead_cross']].iterrows():
ax.annotate('D', xy=(index, row['short_ma']),
xytext=(index, row['short_ma'] - 1500),
size=10, color='blue',
arrowprops={'arrowstyle': '->', 'color': 'blue'})
plt.savefig('cross1.png')
plt.show()
if __name__ == '__main__':
main()
ゴールデンクロス/デッドクロスは正しく求められているようです。
ゴールデンクロス/デッドクロス後の株価の変化率を求める
では、ゴールデンクロス/デッドクロス後の株価の変化率を求めます。ゴールデンクロス後の変化率は次のデッドクロスまでの期間で求めています。反対にデッドクロス後の変化率は次のゴールデンクロスまでの期間で求めています。途中で変化率の要約統計量(平均、最大値、最小値、標準偏差など)を出力しています。最後に見やすいようにグラフ化しています。
import os
import math
import datetime
import numpy as np
import pandas as pd
import pandas_datareader
import talib
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
START_DATE = datetime.date(2011, 1, 1)
END_DATE = datetime.date(2020, 12, 31)
def get_stock(ticker, start_date, end_date):
'''
get stock data from Yahoo Finance
'''
dirname = 'data'
os.makedirs(dirname, exist_ok=True)
fname = f'{dirname}/{ticker}.pkl'
df_stock = pd.DataFrame()
if os.path.exists(fname):
df_stock = pd.read_pickle(fname)
start_date = df_stock.index.max() + datetime.timedelta(days=1)
if end_date > start_date:
df = pandas_datareader.data.DataReader(
ticker, 'yahoo', start_date, end_date)
df_stock = pd.concat([df_stock, df[~df.index.isin(df_stock.index)]])
df_stock.to_pickle(fname)
return df_stock
def pct_change(before, after):
return (after / before) - 1.0
def analyze_golden_cross(df):
'''
ゴールデンクロスの翌日から株価(終値)がどう変化したか求める
デッドクロスになったらそこで処理を終える
'''
results = []
for date, _ in df[df['golden_cross']].iterrows():
result = []
close_at_golden_cross = df.loc[date]['Close']
row = df.index.get_loc(date)
for _, s in df.iloc[row+1:].iterrows():
result.append(pct_change(close_at_golden_cross, s['Close']))
if s['dead_cross']:
results.append(result)
result = []
break
if len(result) > 0:
results.append(result)
fig, ax = plt.subplots(figsize=(12, 8))
for result in results:
ax.plot(result)
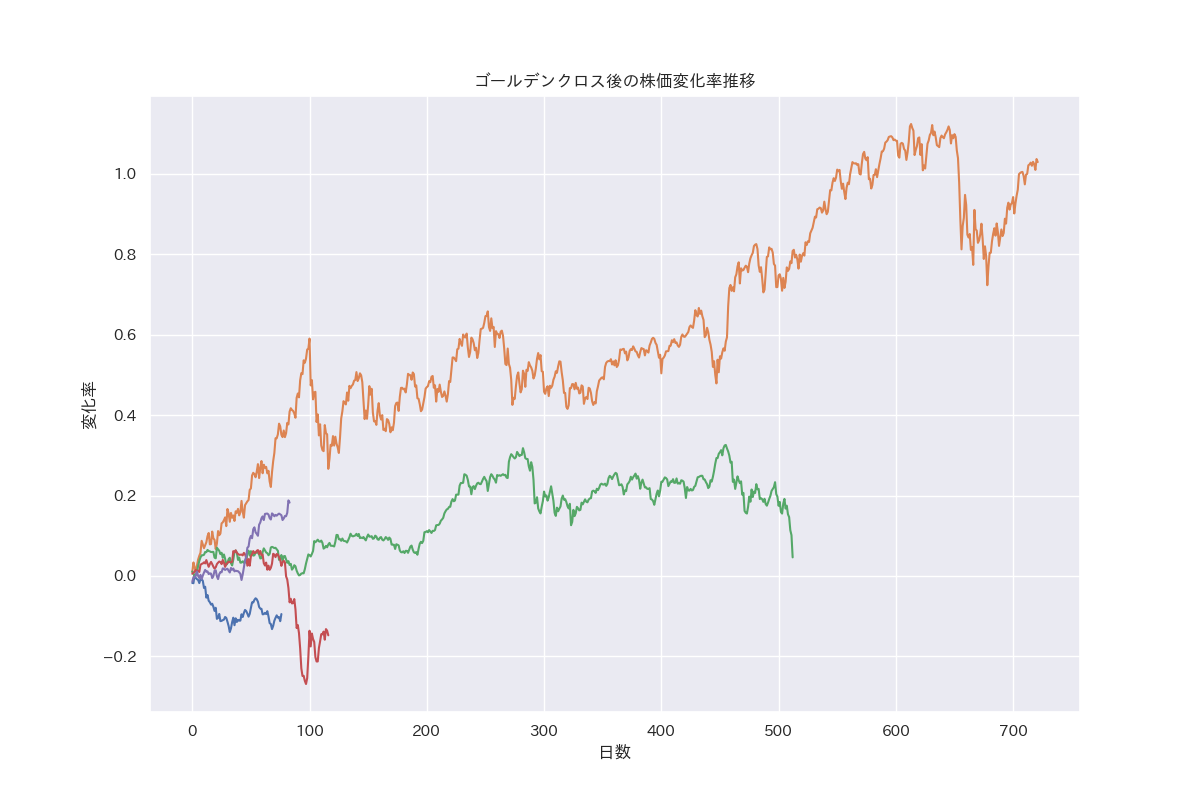
ax.set_title('ゴールデンクロス後の株価変化率推移')
plt.xlabel('日数')
plt.ylabel('変化率')
plt.savefig('cross2-1.png')
plt.show()
# 平均変化率を求める
all_result = []
for result in results:
all_result.extend(result)
all_result = np.array(all_result)
print(pd.DataFrame(all_result).describe())
# 平均変化率の分布図
fig, ax = plt.subplots(figsize=(8, 6))
bins = math.ceil(math.log(len(all_result), 2) + 1)
ax.hist(all_result, bins=bins)
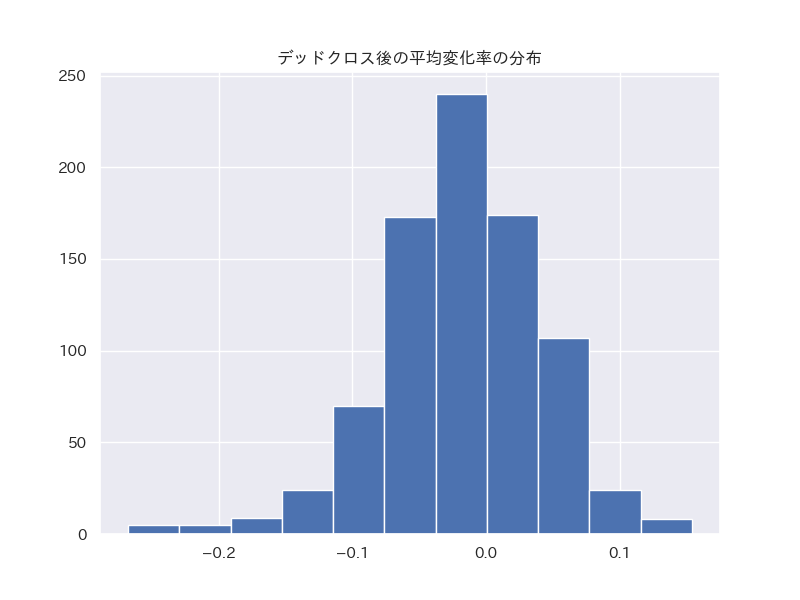
ax.set_title('ゴールデンクロス後の平均変化率の分布')
plt.savefig('cross2-2.png')
plt.show()
def analyze_dead_cross(df):
'''
デッドクロスの翌日から株価(終値)がどう変化したか求める
ゴールデンクロスになったらそこで処理を終える
'''
results = []
for date, _ in df[df['dead_cross']].iterrows():
result = []
close_at_golden_cross = df.loc[date]['Close']
row = df.index.get_loc(date)
for _, s in df.iloc[row+1:].iterrows():
result.append(pct_change(close_at_golden_cross, s['Close']))
if s['golden_cross']:
results.append(result)
result = []
break
if len(result) > 0:
results.append(result)
fig, ax = plt.subplots(figsize=(12, 8))
for result in results:
ax.plot(result)
ax.set_title('デッドクロス後の株価変化率推移')
plt.xlabel('日数')
plt.ylabel('変化率')
plt.savefig('cross2-3.png')
plt.show()
# 平均変化率を求める
all_result = []
for result in results:
all_result.extend(result)
all_result = np.array(all_result)
print(pd.DataFrame(all_result).describe())
# 平均変化率の分布図
fig, ax = plt.subplots(figsize=(8, 6))
bins = math.ceil(math.log(len(all_result), 2) + 1)
ax.hist(all_result, bins=bins)
ax.set_title('デッドクロス後の平均変化率の分布')
plt.savefig('cross2-4.png')
plt.show()
def main():
short_term = 25
long_term = 75
df = get_stock('^N225', START_DATE, END_DATE)
# 移動平均を求める
df['short_ma'] = talib.SMA(df['Close'], timeperiod=short_term)
df['long_ma'] = talib.SMA(df['Close'], timeperiod=long_term)
# クロスしている箇所を見つける
df['diff'] = df['long_ma'] - df['short_ma']
df_cross = df[df['diff'] * df['diff'].shift() < 0]
df['golden_cross'] = df.index.isin(df_cross[df_cross['diff'] < 0].index)
df['dead_cross'] = df.index.isin(df_cross[df_cross['diff'] > 0].index)
sns.set(font='IPAexGothic')
analyze_golden_cross(df)
analyze_dead_cross(df)
if __name__ == '__main__':
main()
ゴールデンクロス後の変化率
-
要約統計量
統計量 値 count 1487.000000 mean 0.080796 std 0.118025 min -0.123680 25% 0.005977 50% 0.050059 75% 0.122404 max 0.709272 -
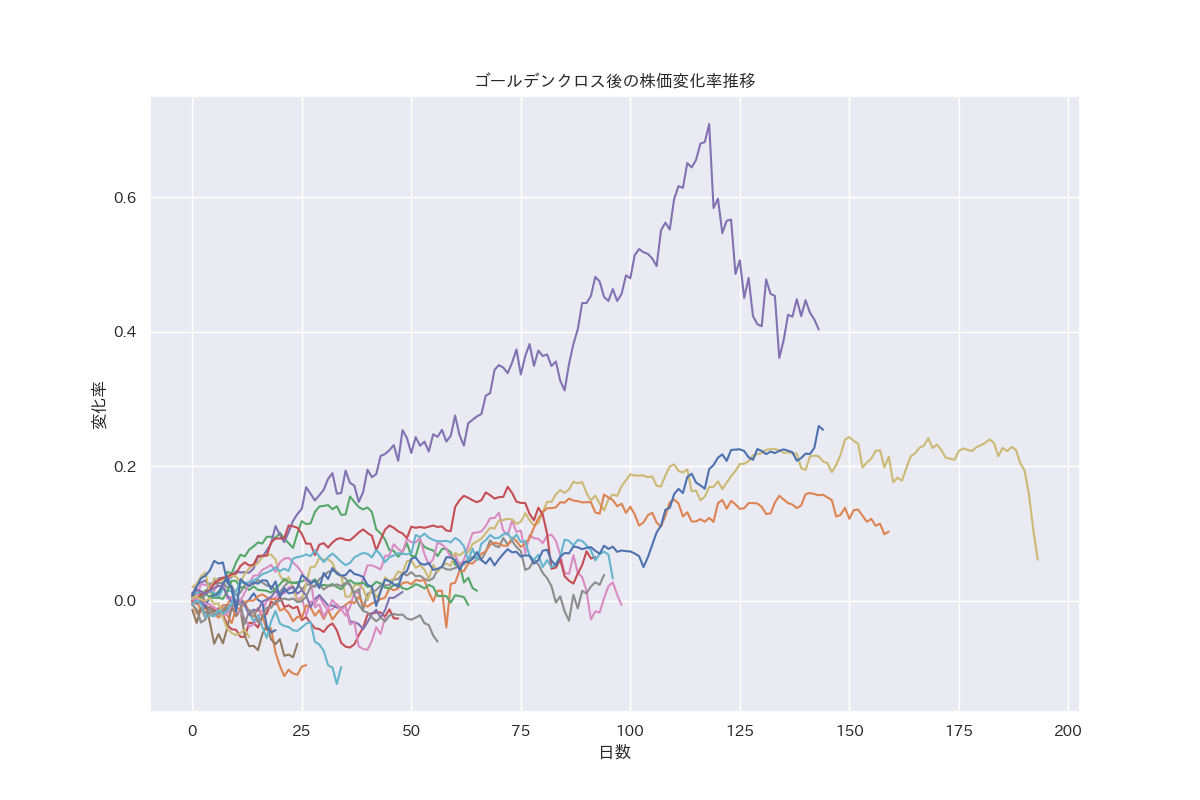
変化率の推移
-
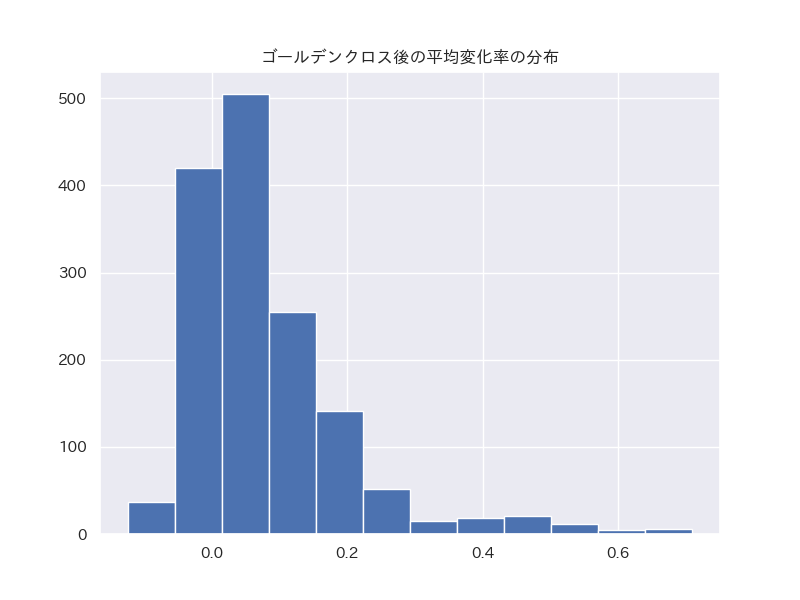
変化率の分布
デッドクロス後の変化率
-
要約統計量
統計量 値 count 839.000000 mean -0.018099 std 0.059415 min -0.267749 25% -0.050816 50% -0.014894 75% 0.020195 max 0.153848 -
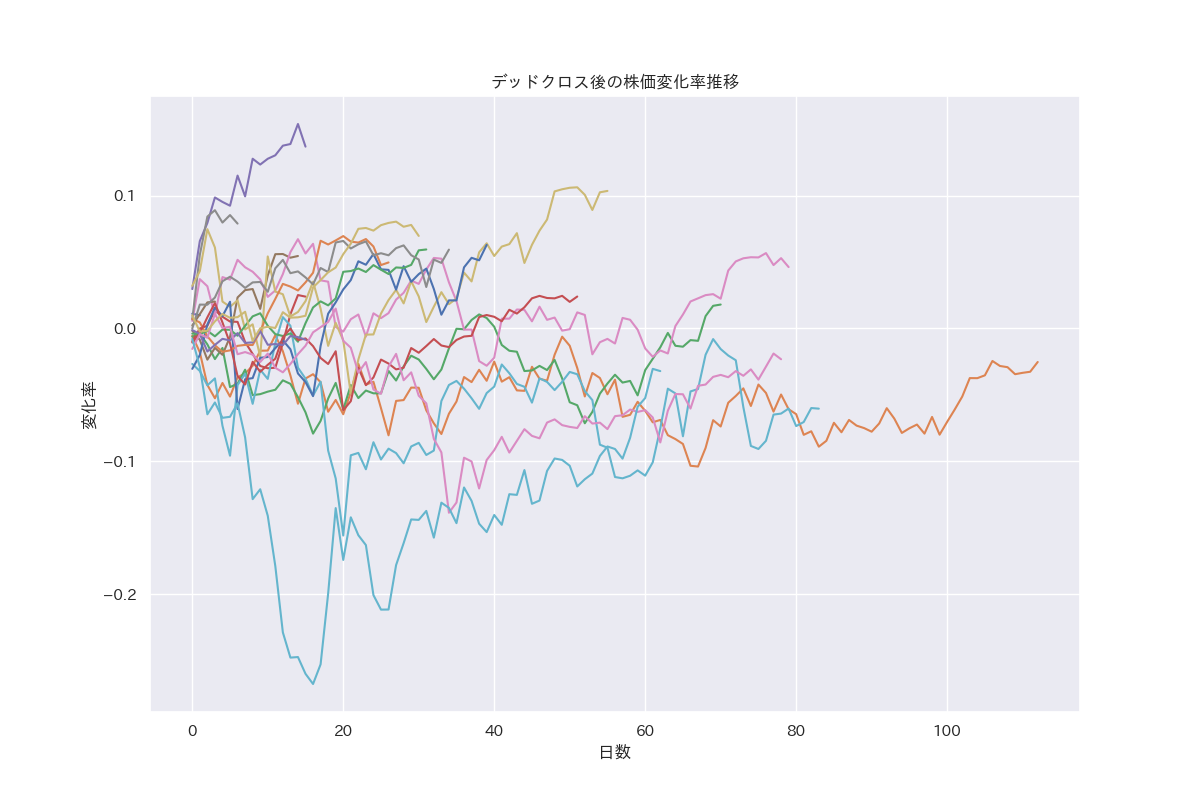
変化率の推移
-
変化率の分布
ゴールデンクロス後の変化率を見ると、大部分がにプラスであることがわかります。変化率を見てもその傾向が見て取れます。平均変化率も8%あります。
デッドクロス後の変化率を見ると、マイナスとなっているものが多いですが、ゴールデンクロスほどの傾向は見られません。変化率の分布も0近辺で高くなっており、平均変化率も1%ほどにとどまっています。
この10年間で株価が約2倍になっていることから、基本的には上昇のトレンドにあったためだと思われます。
短期線、長期線の期間はいくつがよいか
上記は短期線を25日、長期線を75日として計算した結果となります。では、もっとも変化率の大きい短期と長期の期間の組み合わせはいくつになるのでしょうか?上で行った計算を短期を2〜249、長期を3〜250として計算してみます。それぞれの結果から平均変化率を計算し、これをヒートマップにしてみます。ちなみに私のPCではこの計算に3時間かかりました。(もっと早いPCが欲しい...)
import os
import math
import datetime
import numpy as np
import pandas as pd
import pandas_datareader
import talib
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
START_DATE = datetime.date(2011, 1, 1)
END_DATE = datetime.date(2020, 12, 31)
def get_stock(ticker, start_date, end_date):
'''
get stock data from Yahoo Finance
'''
dirname = 'data'
os.makedirs(dirname, exist_ok=True)
fname = f'{dirname}/{ticker}.pkl'
df_stock = pd.DataFrame()
if os.path.exists(fname):
df_stock = pd.read_pickle(fname)
start_date = df_stock.index.max() + datetime.timedelta(days=1)
if end_date > start_date:
df = pandas_datareader.data.DataReader(
ticker, 'yahoo', start_date, end_date)
df_stock = pd.concat([df_stock, df[~df.index.isin(df_stock.index)]])
df_stock.to_pickle(fname)
return df_stock
def pct_change(before, after):
return (after / before) - 1.0
def analyze_golden_cross(df):
'''
ゴールデンクロスの翌日から株価(終値)がどう変化したか求める
デッドクロスになったらそこで処理を終える
'''
results = []
for date, _ in df[df['golden_cross']].iterrows():
result = []
close_at_golden_cross = df.loc[date]['Close']
row = df.index.get_loc(date)
for _, s in df.iloc[row+1:].iterrows():
result.append(pct_change(close_at_golden_cross, s['Close']))
if s['dead_cross']:
results.append(result)
result = []
break
if len(result) > 0:
results.append(result)
# 平均変化率を求める
all_result = []
for result in results:
all_result.extend(result)
return np.array(all_result)
def analyze_dead_cross(df):
'''
デッドクロスの翌日から株価(終値)がどう変化したか求める
ゴールデンクロスになったらそこで処理を終える
'''
results = []
for date, _ in df[df['dead_cross']].iterrows():
result = []
close_at_golden_cross = df.loc[date]['Close']
row = df.index.get_loc(date)
for _, s in df.iloc[row+1:].iterrows():
result.append(pct_change(close_at_golden_cross, s['Close']))
if s['golden_cross']:
results.append(result)
result = []
break
if len(result) > 0:
results.append(result)
# 平均変化率を求める
all_result = []
for result in results:
all_result.extend(result)
return np.array(all_result)
def main():
df = get_stock('^N225', START_DATE, END_DATE)
sns.set(font='IPAexGothic')
golden_cross_result = []
dead_cross_result = []
for long_term in np.arange(3, 251):
for short_term in np.arange(2, long_term):
# 移動平均を求める
df['short_ma'] = talib.SMA(df['Close'], timeperiod=short_term)
df['long_ma'] = talib.SMA(df['Close'], timeperiod=long_term)
# クロスしている箇所を見つける
df['diff'] = df['long_ma'] - df['short_ma']
df_cross = df[df['diff'] * df['diff'].shift() < 0]
df['golden_cross'] = df.index.isin(
df_cross[df_cross['diff'] < 0].index)
df['dead_cross'] = df.index.isin(
df_cross[df_cross['diff'] > 0].index)
result = analyze_golden_cross(df)
golden_cross_avg = np.average(result)
golden_cross_result.append(
{'long': long_term, 'short': short_term, 'avg': golden_cross_avg})
result = analyze_dead_cross(df)
dead_cross_avg = np.average(result)
dead_cross_result.append(
{'long': long_term, 'short': short_term, 'avg': dead_cross_avg})
print(
f'long={long_term}, short={short_term}, g-avg={golden_cross_avg}, d-avg={dead_cross_avg}')
# 移動平均期間の組み合わせによる変化率(ゴールデンクロス)
results = pd.DataFrame(golden_cross_result).pivot('short', 'long', 'avg')
fig, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(results, square=True, cmap='Reds', ax=ax)
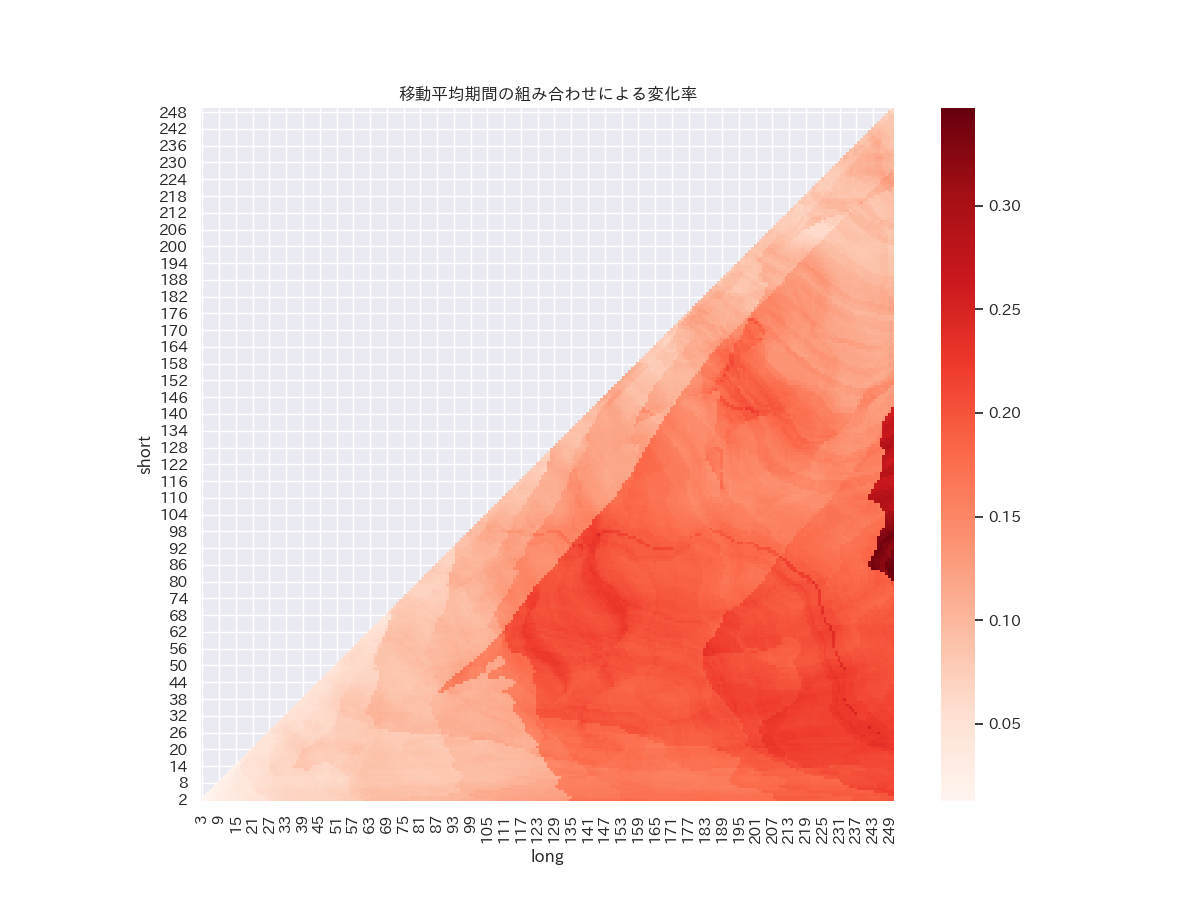
ax.set_title('移動平均期間の組み合わせによる変化率(ゴールデンクロス)')
ax.invert_yaxis()
ax.grid()
plt.savefig('cross3-1.png')
plt.show()
# 移動平均期間の組み合わせによる変化率(デッドクロス)
results = pd.DataFrame(dead_cross_result).pivot('short', 'long', 'avg')
fig, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(results, square=True, cmap='Blues_r', ax=ax)
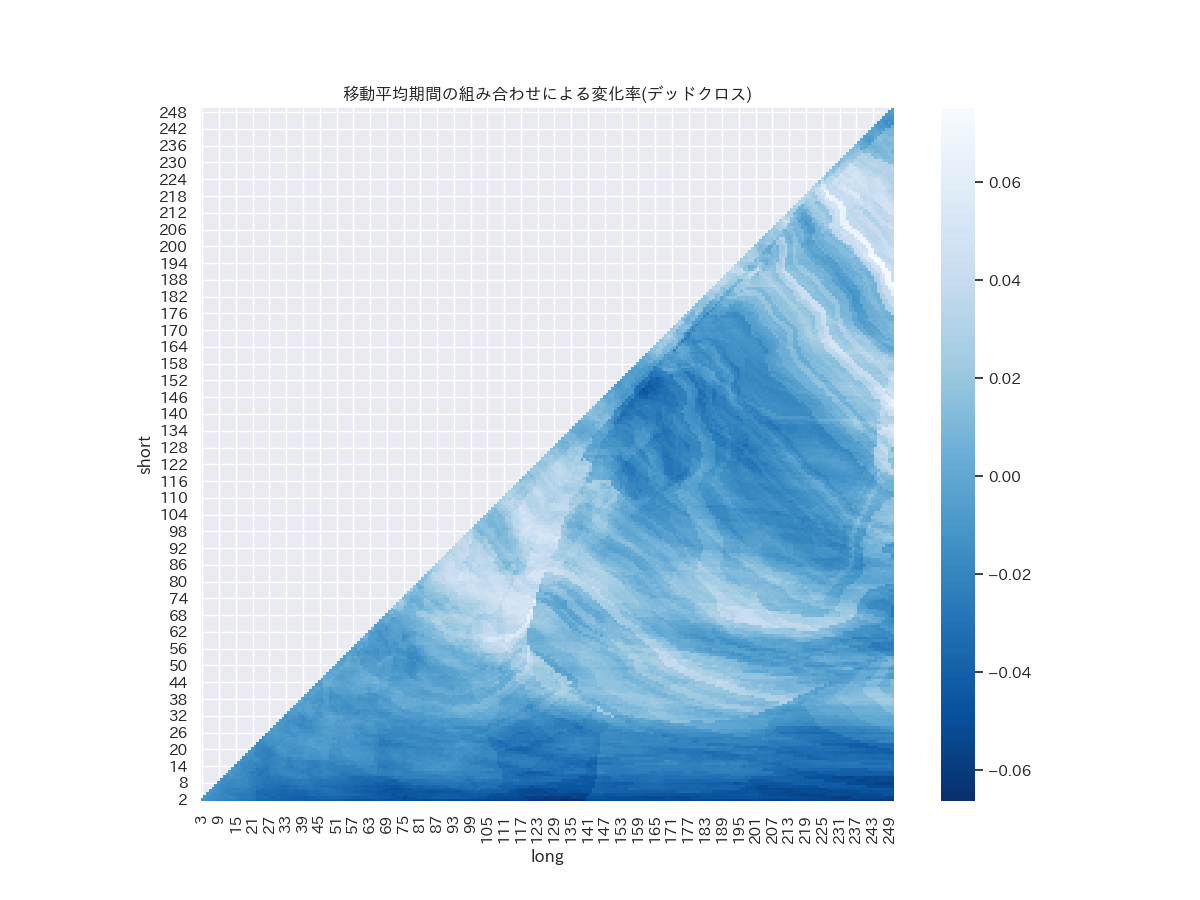
ax.set_title('移動平均期間の組み合わせによる変化率(デッドクロス)')
ax.invert_yaxis()
ax.grid()
plt.savefig('cross3-2.png')
plt.show()
if __name__ == '__main__':
main()
-
ゴールデンクロス後の変化率
濃い赤が変化率の大きい部分を表しています。上記の短期25日、長期75日のところを見ると、そんなに大きな変化率ではないことがわかります。このグラフだと、短期100日くらい、長期250日くらいところの変化率が非常に大きいです。最大変化率は34.7%です。詳しくは見れていませんが、期間が長くなるとゴールデンクロス/デッドクロスの回数も少なくなり、データが偏っているのではないかと思われます。最大変化率34.7%のときの短期線は85日、長期線は249日です。このときの変化率の推移を見てみます。(プログラムは2つ目のプログラムで期間を変更したものとなります。) 最大変化率は100%を超えてます!ただサンプル数が少なすぎますね。
-
デッドクロス後の変化率
こちらはゴールデンクロス後ほど色の変化がありません。このグラフでは白が変化率0%が白でないのでわかりにくいですが、変化率がプラスとなっているところもたくさんあります。
最後に
今回はSMAを使用してゴールデンクロス/デッドクロス後の株価の変化を調べてみました。ゴールデンクロスで株を購入すればプラス8%の変化が期待できる、逆にデッドクロスで株を手放せばマイナス1%の変化を回避できる、と言えると思います。つまりゴールデンクロス/デッドクロスを指標とすることは有効ということです。ただし、今回求めているのは変化率であって利益ではありません。次回は利益がどれくらいになるのかを計算してみたいと思います。
ソースはGitHubに置いてあります。
- 2020/04/13 アップロードしたグラフが間違っていたので修正しました。また変化率が最大となる短期線、長期線での変化率のグラフを追加しました。