はじめに
こんにちは、@mahiro0x00 です。
この記事では検索の自動補完機能について、どのような仕組み/実装で動いているのかコードベース(Python)も利用して解説していきたいと思います。
検索の自動補完とは
自動補完とは、文字列の入力をした時に、次に連なる字句を推測して候補を表示する機能です。オートコンプリートとも呼ばれます。
有名なものを挙げるとGoogleの検索画面に使われている自動補完です。例えば以下のように"ハッカソ"という文字列を入れると、それに続く可能性の高いワードが候補として表示されていますね。
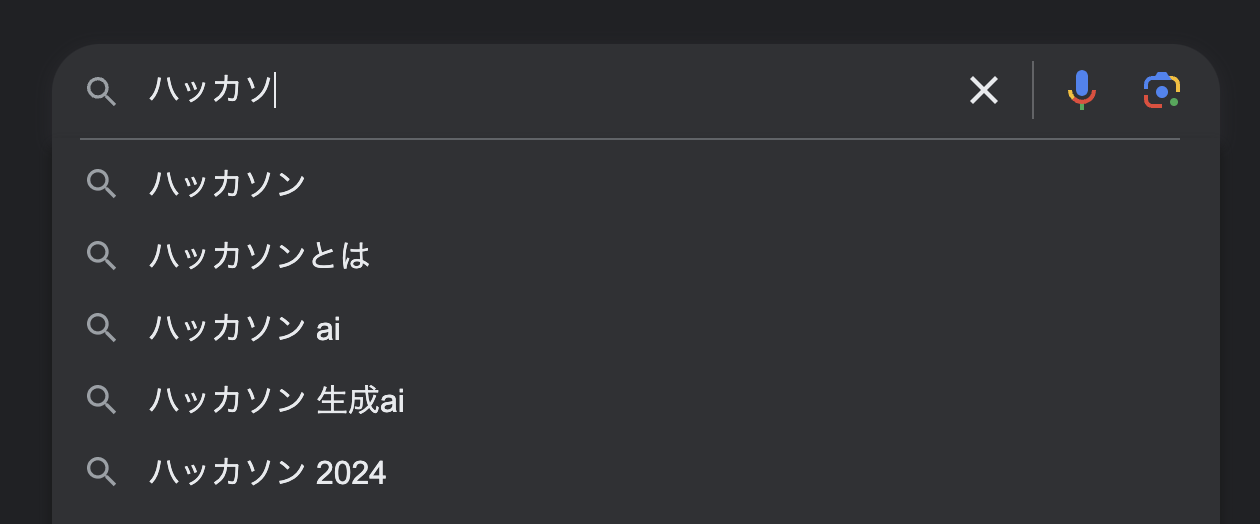
どのように作るか
何も考えず愚直に実装すると以下のようなSQLが書けそうです。wordsテーブルには一般的な単語の一覧や、過去に検索されたことのあるワードが入っています。
SELECT word FROM words WHERE word LIKE 'ハッカソ%' LIMIT 5;
これで"ハッカソ"と入力した際に"ハッカソ"から始まる他の単語を5つ候補として表示できるわけですが、以下のような問題があります。
- 計算量がO(length(words)) になってしまう
- 適切にindexを貼るとある程度改善できそう
- 単語が最初にヒットした5件のみが表示され、その単語の検索頻度などは考慮されていない
- 例えば"ハッカソ"とうってハッカソンなど検索されそうなワードがでてきたらユーザとしては使いやすいが、ハッカソウ(植物)のような普段使わない単語が候補に出てくる可能性がある (どちらも普段使わないかもですがw)
UX向上のためにユーザが検索しそうなワードを自動補完する設計を考えると、例えばwordとそのwordの検索された回数を利用し、集計して上位 k件を返却して表示する、などが考えられます。
しかし検索のたびに集計が走ってしまうとパフォーマンスはあまり良くないです。RDBで検索クエリの上位 k件を表示するのは非効率ともいえます。(集計テーブルを事前に用意するのも手段の1つですが、この手法との比較は後述します)
これらの問題を解決するデータ構造があります。本記事の主役であるトライデータ構造です。
トライデータ構造
トライデータ構造とは、文字列をコンパクトに格納できるツリー状のデータ構造です。
名前の由来はretrieval(検索) で、その由来のとおり文字列の検索操作のために設計されています。
以降では実際のデータと図を用いてより具体的な説明をします。
例えば以下のような単語とその検索頻度の集計されたデータがあるとします。
data = {
"tree": 10,
"true": 35,
"try": 29,
"toy": 14,
"wish": 25,
"win": 50
}
これをトライデータ構造で表現すると以下の図のようになります。
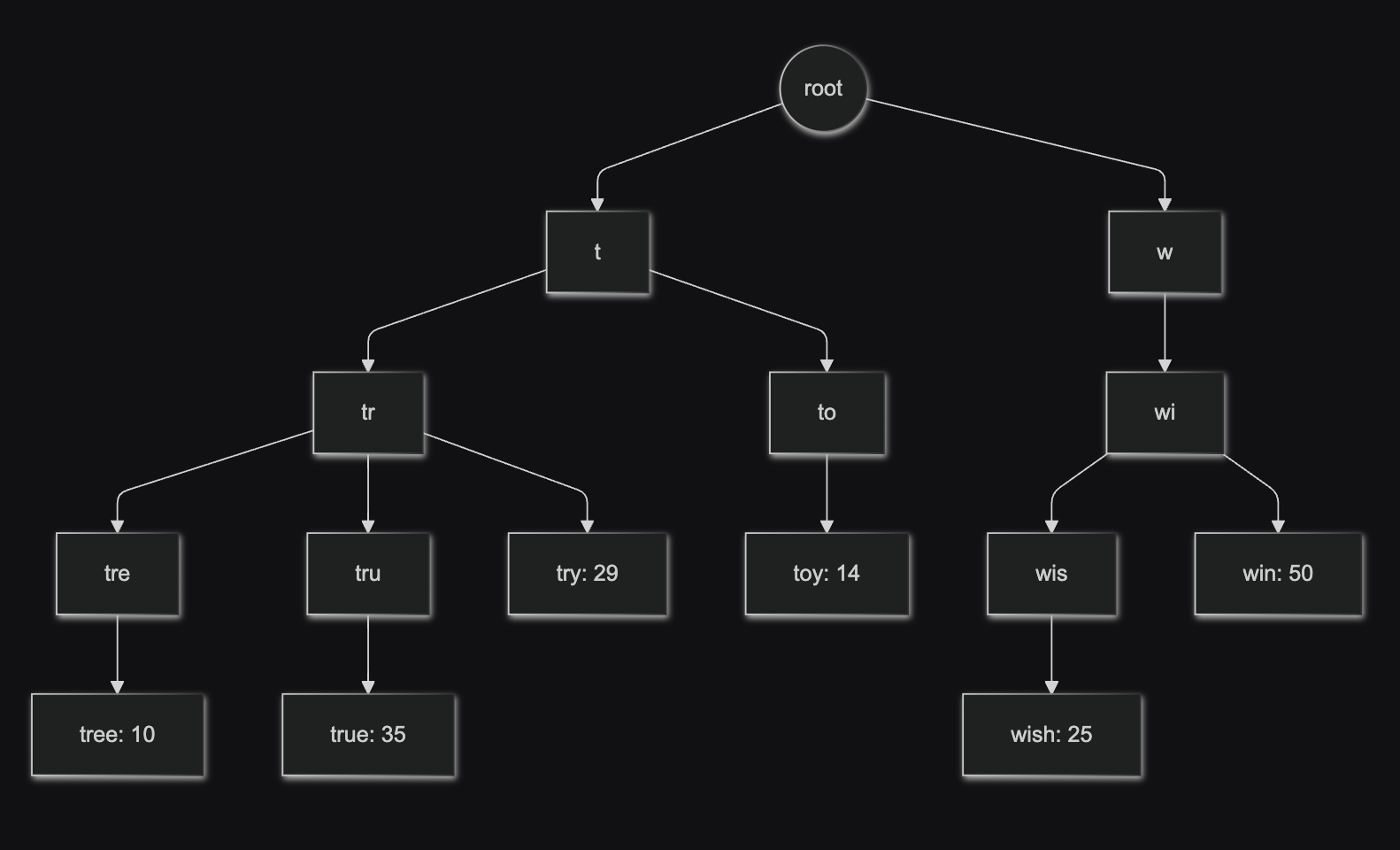
例えば"tr"という文字をユーザが検索クエリとして検索した場合、トライデータ構造では上からtrに一致するノードを探索し、発見後はそのノードの子にあたるノードを全て探索しそれぞれの単語と頻度を取得後、上位 k件(図ではk=2)を抽出して返却します。

この時計算量は以下の合計値となります。
- 接頭辞("tr")を発見する計算量 O(length("tr"))
- 子ノードを取得する計算量 O(c) c=あるノードの子ノードの数
- 取得した子ノードをソートし k件取得する O(c logc)
ただしこの実装を用いても毎回子ノードの探索やそのソートが行われるため、まだ高速化の余地があります。
各ノードにキャッシュを導入する
トライデータ構造の各ノードに頻度とtopKのキャッシュを導入することでさらなる高速化を目指します。

上記のように各ノードにtop2のキャッシュを持たせてみました。例えば"tr"という検索クエリを受け取った場合、以前まではその子ノードの探索と取得後のソートがありましたが、事前に計算してその結果をノードで保持しておくことでO(1)まで抑えられます。
この設計により構築時のコストは大きくなりますが、検索時のO(1) + O(length("tr")) 程度まで高速化ができました。
(この記事では詳細まで書きませんが、接頭辞とノードを紐づけて保持しておくことで対象ノードの探索もO(1)に抑えられるので O(1)での検索も実現可能かと思います)
実装ベースの解説
実装の全体像はこちら
https://gist.github.com/mahiro72/4acf4668f20b648c72212f2d760b650c
この記事ではメインとなるトライデータ構造の構築と、検索時のメソッドについて紹介します。
TrieとTrieNode
今回使うクラスは2つです。Trieがトライデータ構造の全体です。ルート情報のみを持ち、そのルートノードが多くの子ノードを持っています。
TrieNodeはノードの実態を表しており、子ノードの情報や検索頻度、単語の終端であるか(例えばtruなど中途半端な文字列ではなく、trueのような文字列の最後であるか) といった情報を保持しています。
class TrieNode:
def __init__(self):
self.children: Dict[str, TrieNode] = {} #子ノード
self.is_end = False # 単語の終端か
self.freq = 0 # 検索頻度
self.top_words: Dict[str, int] = {} #topKのキャッシュ
class Trie:
def __init__(self, k: int = 5):
self.root = TrieNode() # トライデータ構造のroot
self.k = k # topKのキャッシュを各ノードで保持
...
トライデータ構造の構築
構築時は単語(word)とその検索頻度(freq)を引数として渡します。
渡された単語が"true"だった場合、t,r,u,eの4つのノードが作成されます。(図と同様の表現をするとt,tr,tru,trueです)
それぞれのノードは親と子として紐づかれていきます。root-t, t-r, r-u...といったイメージです。
その後単語の終端であるeまで到達したら フラグを立て、頻度を設定します。
最後にキャッシュの設定です。reversedを利用し一番下の子ノードから順にキャッシュを更新してきます。例えば最後であるeの場合は頻度のみ設定({true: 35}のイメージ) され、次にその親であるuはuの持つ子ノードのキャッシュを全て取得 && それをmergeし、新たなキャッシュを再作成します。このように子から親に向かってキャッシュを再作成していき、e,u,r,t,rootのキャッシュが全て更新されます。
def _insert_with_freq(self, word: str, freq: int):
node = self.root
path_nodes = [node] # 今回入れた単語のノードが入っている。例だとroot, t,r,u,eの5つのノード
# t,r,u,eの4つのノードが作成され、それぞれの子ノードとして紐づけられていく
# たとえばtの子ノードとしてrが設定される
for char in word:
if char not in node.children:
node.children[char] = TrieNode()
node = node.children[char]
path_nodes.append(node)
# 単語の終端をマークする
# 今回の例では eのノード(trueのノード) のis_endがTrueになる
node.is_end = True
node.freq = freq
# パス上の全ノードのtop_wordsキャッシュを更新
for n in reversed(path_nodes):
merged_words = {} if len(n.top_words) == 0 else n.top_words.copy()
if n.is_end:
merged_words[word] = freq
else:
for child in n.children.values(): #自身が単語の終端ではない場合、子ノードのtop_wordsをマージする
for w, f in child.top_words.items():
merged_words[w] = f
n.top_words = dict(sorted(merged_words.items(), key=lambda x: (-x[1], x[0]))[:self.k])
検索
検索処理はシンプルです。prefixに検索したいワードを入れて、その文字を1つずつ取り出し子ノードを探索してきます。ヒットしたらそのnodeのキャッシュであるtop_wordsを返却します。
def find_top_k_prefixes(self, prefix: str):
node = self.root
for char in prefix:
if char not in node.children:
return []
node = node.children[char]
# ヒットしたノードのtop_wordsのキャッシュを返す
return node.top_words
キャッシュを導入したことによる課題
キャッシュを導入したことによる課題として、更新が手間な点があげられます。
例えば trueという単語の検索頻度を1増やしたい場合は、t,r,u,e全てのノードの再計算が必要です。
そのためこの設計は頻繁に検索頻度を更新するケースには適しておらず、定期的なデータバッチによってトライ構造を毎回新規作成し高速な検索機能を実現するために使われる想定です。
プロダクション環境での運用
プロダクション環境で運用していくには、インメモリだけで工夫して運用するパターンや、大規模なサービスになるとトライデータ構造の実態を永続化できるストレージにおいて、Redisなどのキャッシュストアでそのキャッシュを保持する、といったパターンもありそうです。
また、ElasticSearchといった外部サービスに検索機能の実現を委ねるのも一つの手です。
おまけ
今回のトライ構造について、RDBでも事前に集計テーブルを作成することで同様の仕組み自体は実現可能です。
ではRDBで実現したほうがいいのでしょうか?
結論からいうとユースケースによります。
一般的な検索システムを自前で用意する場合はRDBでも工夫次第で十分実現できるかと思います。一方限定的なユースケースではトライ構造を使った方が良い時もあります。
例えば本記事のメインテーマでもある検索の自動補完です。
検索の自動補完では、主に以下のような要件が求められます。
- 超低レイテンシーであること
- 大量の同時リクエストを処理できること
今回紹介したトライデータ構造は、インメモリ(もしくはRedisなどのキャッシュ) から返却するためレイテンシーが低い点、また、ノードごとにトップKを保持する仕組みによって、大量の同時リクエストがあってもキャッシュされた候補を即時に返却できるのも大きな強みです。
もちろんRDBの集計テーブルとしてプレフィックスのトップKを持つことで似た機能の実現は可能ですが、SQL処理やネットワーク通信のオーバヘッドを考慮すると、トライデータ構造の方が有利だといえます。
おわりに
普段から無意識に使っている自動補完ですが、中を見てみると面白い技術とさまざまな工夫がありましたね。この記事が少しでも誰かの参考になったら幸いです。