Mag Beginner Contest 002
5/12 00:00 〜 5/13 00:00 にかけて行われたプログラミングコンテストです。
皆さんお疲れ様でした。
#1 - Seeking for Cat
FA: milkcoffee さん
英小文字からなる文字列 $S$ が与えられます。
この中に部分文字列 nyan が何個含まれているか数えてください。
- $1 \le |S| \le 1000$
ZONeエナジープログラミングコンテストのA問題が元ネタです。
上の問題では、例えば Python なら S.count("ZONe") といった解き方が可能です。
しかし、この問題で S.count("nyan") とした場合は S = "nyanyan" のような場合に $1$ と答えてしまいます。
sum(S[i:i+4] == "nyan" for i in range(len(S) - 4 + 1)) のように、ループで数えるのがよいでしょう。
#2 - Harmonic Number
FA: milkcoffee さん
$N$ 番目の調和数を $\text{mod }998244353$ で答えてください。
- $1 \le N \le 10^6$
この記事そのものです。
C++ などの高速な言語では $O(N \log N)$ でも解けますが、 CPython では $O(N)$ で計算しないと TLE するはずです。
#3 - Pair of Coprime Numbers
FA: shakayami さん
$N$ 以下の互いに素な正整数のペア ${x, y}$ の個数を求め、 $\text{mod }998244353$ で答えてください。
- $1 \le N \le 5 \times 10^5$
想定解1 $O(N \log \log N)$
$N$ 以下の互いに素な自然数のペアの個数は、オイラーの $\phi$ 関数を使って $\sum_{i=1}^{N} \phi(i)$ と書くことができます。
$\phi(i) \quad (i = 1, 2, \ldots, N)$ は、エラトステネスの篩のようにすることで $O(N \log \log N)$ で求めることができます。
想定解2 $O(N \log N)$
前処理として、エラトステネスの篩を使って最小素因数のテーブルを $O(N \log \log N)$ で作成します。
$i = 1, 2, \ldots, N$ について、素因数分解しながら $\phi(i)$ を求めると、ひとつあたり $O(\log N)$ 、全体では $O(N \log N)$ で求めることができます。
#4 - Clash of Triangles
FA: riantkb さん
大変申し訳ございませんでした。
この問題にはテストケースのミスと制約違反があったため 1 点になりました。
- テストケースのミス:答えが誤っていた。
- 制約違反の内容:必ず衝突するという制約があったが、衝突しない入力が存在した。
三角形 $A, B$ があります。
$B$ が今速度 $\boldsymbol{v}$ で等速直線運動をはじめました。
$B$ が $A$ と衝突するまでの時間を求めてください。
当初の想定解
重心が一番近くなるときを上限として、三角形が重なっているかで二分探索をする。
三角形が重なっているかどうかは、以下の2つの点の少なくともどちらかであるときです。
- 片方の点がもう片方に含まれている
- 片方の辺がもう片方の辺と交差している
残念ながらこの想定解がバグっていたのか、実装がバグっていたのかわかりませんがテストケースが壊れていました。
正しい解法
もし $A, B$ が初期状態で衝突しておらず、後で衝突するときを考えます。
$A$ のある辺について、始点の位置ベクトルを $\boldsymbol{a}$ 、そこから終点までのベクトルを $\boldsymbol{u}$ とします。
$B$ のある頂点の位置ベクトルを $\boldsymbol{b}$ 、 $B$ が移動する速度のベクトルを $\boldsymbol{v}$ とします。
$A$ の辺と $B$ の頂点が衝突すると考えたとき、衝突する点は変数 $t, s$ を用いて $\boldsymbol{a} + s \boldsymbol{u} = \boldsymbol{b} + t \boldsymbol{v}$ と表せます。
この式は二元一次連立方程式であるため、行列計算によって $s, t$ を求めることが可能です。
このとき、 $0 \le s \le 1$ かつ $t \ge 0$ なら実際に時間 $t$ で衝突していると考えられます。

これを $A$ のすべての辺と $B$ のすべての頂点について行います。
次に、同じことを、 $A$ が速度 $-\boldsymbol{v}$ で $B$ に向かっていると考えて、 $A, B$ を逆にして行います。
これによって衝突する最短の時間がわかります。
ただし、 $A, B$ が初期状態で衝突している場合は、この判定法ではうまくいきません。
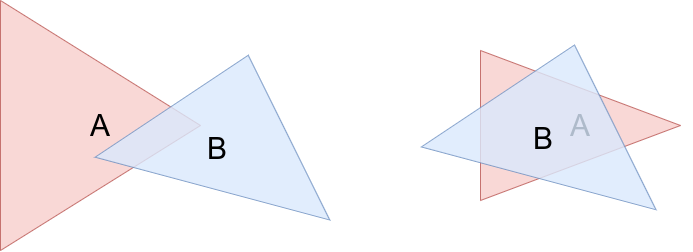
例えば次のような場合を考えてみましょう。
この例では頂点と辺がくっついているわけではないため、上で述べた解き方では正しい衝突までの時間が出ません。
そこで、当初の想定解の部分で述べた、三角形が重なっているか判定する方法を使い、重なっていれば 0 を出力します。
計算量は $O(1)$ です。
#5 - Takahashi is Nervous
FA: noimi さん
$N$ 頂点 $M$ 辺の連結な無向グラフがあります。
頂点 $1$ から頂点 $N$ への長さが $L$ の倍数になる最短パスを求めてください。
- $1 \le N, M \le 500$
- $1 \le L \le 100$
この問題ではグラフにそのまま最短距離のアルゴリズムを適用しても答えを求めることができません。
そこでグラフの頂点を $L$ 倍し、頂点 $(v, r)$ に頂点 $v$ までの距離を $L$ で割ったあまり $r$ の情報をのせることにします。
頂点 $(1, 0)$ から頂点 $(N, 0)$ までの最短距離をダイクストラ法で求めることで、 $O((M+N) L \log(NL))$ で答えを求めることができました。
#6 - Sum is X, Min is Y
FA: noimi さん
非負整数からなる集合 $A$ があります。
$A$ の空でない部分集合 $S$ のうち、 $\sum_{x \in S} x \equiv X \mod 1009$ かつ $\min S = Y$ となるものの個数を求めるクエリが $Q$ 個与えられます。
クエリに答えてください。
- $1 \le N \le 1000$
- $1 \le Q \le 10^5$
$dp[i][j] =$ 先頭から $i$ 個見たとき、和が $j$ になる部分集合の個数
という DP の配列をつくります。
すると、 $dp[i][j] - dp[i - 1][j]$ = $i$ 番目で終わり、和が $j$ になる部分集合の個数
となります。
このとき $A$ を降順にソートしておくことで、 $i$ 番目で終わる $\Leftrightarrow$ $i$ 番目の要素が最小となります。
これより、クエリあたり $O(1)$ で求めることができました。