ZONe mad_hacker

2021/04/27 に発売されたエナジードリンクで、缶には何やらプログラムが書かれています。

⚠️hacked⚠️hacked⚠️

究極の没入マッドネスを体感せよ👁

ZONe mad_hacker; 登場

⚠️hacked⚠️hacked⚠️#ZONeエナジー #madhacker pic.twitter.com/QnK53WoII0
— ZONe Energy (@zone_energy_jp) April 26, 2021

何が書かれているのか？

どうやら JavaScript で書かれているようです。

気になったのでRubyに翻訳してみました！¹²

binarySearch
bubbleSort
dpFib
GCD
linearSearch
bfs
mergeSort

まだ全て書けたわけではないですが、ゴールデンウィークなのでどんどん書いていきたいです。

binarySearch (二分探索）

図書館で本を探したことがあるでしょうか。
また、家の本棚から本を探したことがありますか？

図書館では本は著者名の順に並んでいます。あなたの家の本棚ではどうでしょうか。

本が何かの順番に並んでいれば、適当な本を取り出したとき、

それが探している本よりも右にあるならそれより左だけを探せばいい
それが探している本よりも左にあるならそれより右だけを探せばいい

というふうに探すと効率的です。

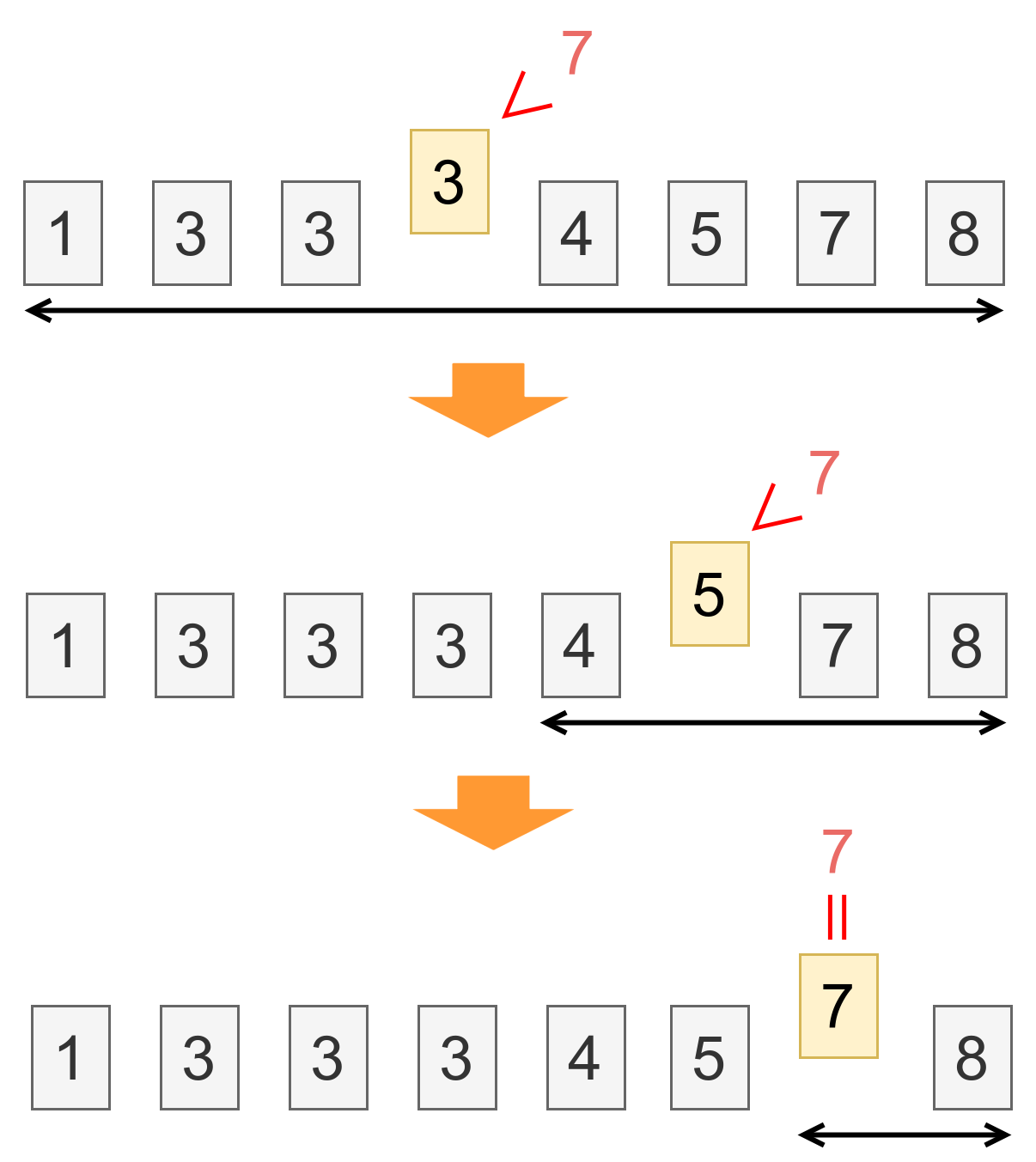
二分探索では、「適当な本」として探す範囲の中央を取ります。
これにより、探す範囲は半分、半分、また半分とどんどん狭くなっていきます。
例えば、探す範囲の長さが $64$ なら、 $64, 32, 16, 8, 4, 1$ となります。
このようにどんどん狭めることで、莫大な長さの配列（例えば、長さが $10^9 = 1,000,000,000$ ）からも、少ない回数（この例では最大 $30$ 回）の探索で $val$ を見つけることができます。

関数 binary_search は、配列 $arr$ の $[min, max]$ の範囲から $val$ という値を探します。
配列 $arr$ はソートされている（順番に並んでいる）必要があります。
$val$ が $arr$ の中にあるなら、その位置を返します。
もし $val$ が $arr$ の中になければ、 nil （「ない」という意味）を返します。

def binary_search(arr, val, min = 0, max = arr.size - 1)
  return nil if max < min                    # もはや探すべき範囲はない
  half = min + (max - min) / 2               # max と min の中間の点
  return half if arr[half] == val            # 見つけた
  (val < arr[half]) ?                        # 中間の点が val よりも右側か？
    binary_search(arr, val, min, half - 1) :   # そうなら、中間よりも左側を探す
    binary_search(arr, val, half + 1, max)     # そうでなければ、中間よりも右側を探す
end

bubbleSort (バブルソート)

書類がバラバラな順番で積まれていて、これを通し番号の順に並べ替える必要があるとします。
あなたならどのように並べ替えますか？

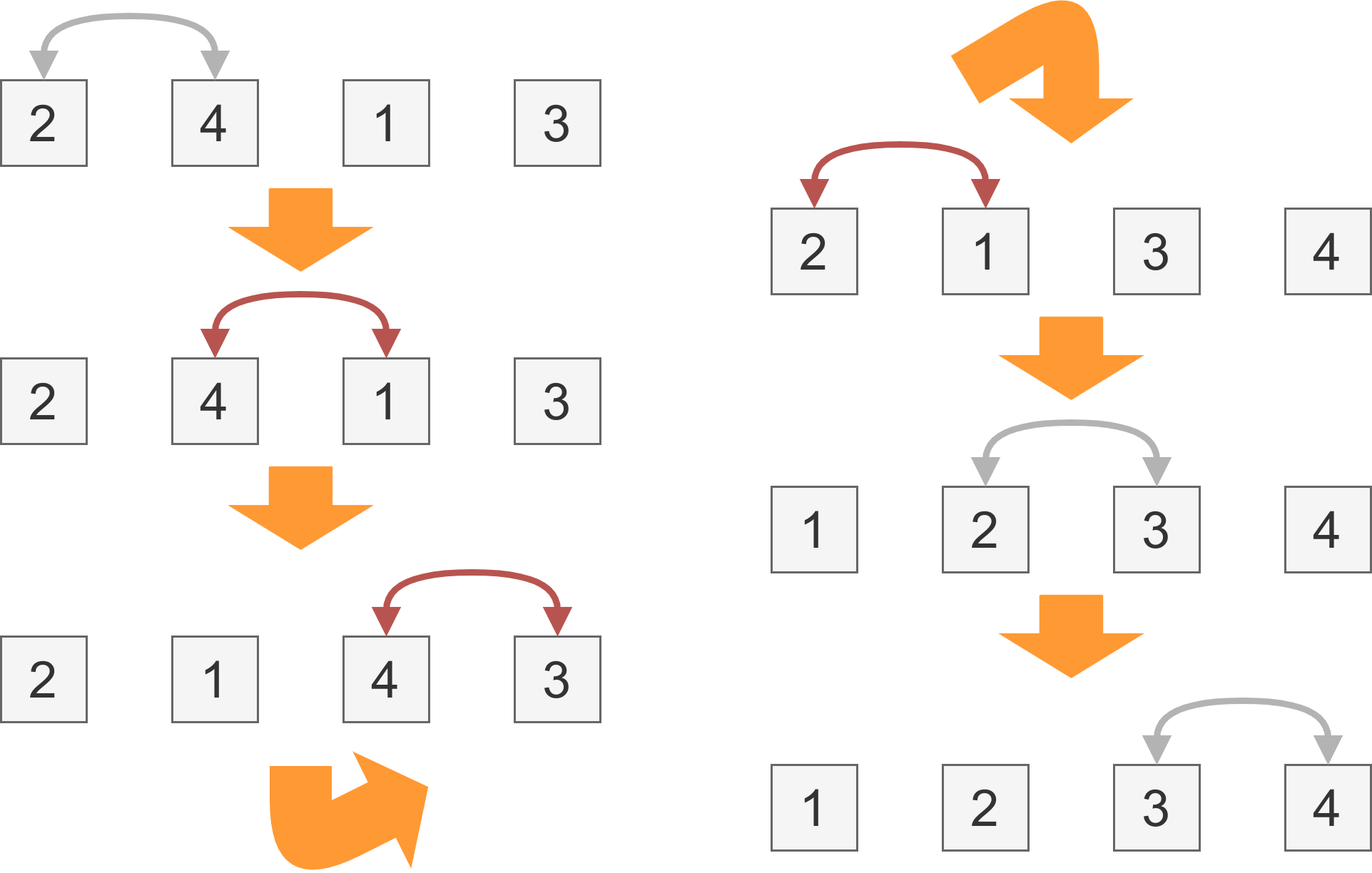
書類を並べ替える（ソートする）一つの方法は、「バブルソート」です。

バブルソートでは、隣り合う $2$ 枚の書類を選び、それが逆順に並んでいたら入れ替えます。

残念ながらバブルソートはあまり効率的なアルゴリズムではなく、要素数の $2$ 乗に比例した回数の比較が必要です。例えば、 $1,000$ 枚の紙があれば、およそ $1,000,000$ 回近くの比較が必要になります。

さらに効率的なマージソートを後で紹介します。

関数 bubble_sort(arr) は配列 $arr$ を昇順に並び替えた後の配列を返します。

def bubble_sort(arr)
  new_arr = arr.dup                                       # arr を複製する
  len = new_arr.size                                      # 配列の長さ
  (0 ... len).each do |i|                                 # len 回繰り返す
    (0 ... len - 1).each do |j|                             # len - 1 回繰り返す
                                                              # 隣り合う 2 要素が逆順になっていたら入れ替える
      new_arr[j], new_arr[j + 1] = new_arr[j + 1], new_arr[j] if new_arr[j] > new_arr[j + 1]
    end
  end
  new_arr                                                 # 新しい配列を返す
end

ちなみに、ある配列に対する、バブルソートをしたときの交換回数を転倒数と呼びます。
競技プログラミングでは転倒数に関する問題が出ることもあります。

dpFib (フィボナッチ数列)

フィボナッチ数列を知っていますか？僕は知っています。

……という冗談はさておき、フィボナッチ数列は $0, 1, 1, 2, 3, 5, \ldots$ という数列で、自然界のいたるところに現れます。
例えば、花びらの枚数など³。

フィボナッチ数の一般項は以下のように求められます⁴。
$$F_n = \frac{\phi^n - (1 - \phi)^n}{\sqrt5}$$
式の中に黄金比 $\phi = \frac{1 + \sqrt5}{2}$ が現れているのがわかりますね。

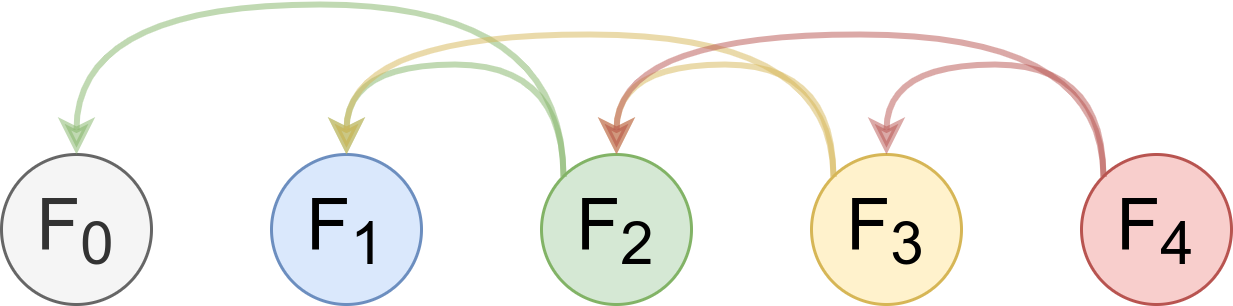
フィボナッチ数は以下のような漸化式を使っても求めることができます。

$$\begin{aligned} F_0 &= 0 \\ F_1 &= 1 \\ F_n &= F_{n - 2} + F_{n - 1} \quad (n \ge 2) \end{aligned}$$

下に示すプログラムでは、この漸化式をそのまま使ってフィボナッチ数を計算しています。

ナイーブなプログラム

def fib(n)
  return 0 if n == 0
  return 1 if n == 1
  fib(n - 2) + fib(n - 1)
end

しかしこのプログラムでは、困ったことに、計算回数が $\phi^{n-1}$ に比例する回数になってしまいます。
たとえば fib(10) は $177$ 回、 fib(20) は $21,891$ 回、 fib(30) は $2,692,537$ 回です。
この調子で計算していては、 fib(100) の計算など、どれだけ時間がかかるか分かったものではありません。

そこで使われるプログラミング的テクニックが動的計画法 (DP: Dynamic Programming)です。
動的計画法では、フィボナッチ数の計算において、それぞれの fib(n) の値を覚えておきます。
このようにすることで、 $n$ 番目のフィボナッチ数の計算に必要な計算回数を $n$ に比例する回数にできます。

ZONe mad_hacker の缶に書かれているコードには動的計画法の書き方の一つ、メモ化再帰と呼ばれる手法が使われています。

関数 dp_fib(n) は $n$ 番目のフィボナッチ数を計算して返します。

def dp_fib(n, memo = {})
  return memo[n] if memo[n]                             # メモがあればそれを返す
  return 0 if n == 0                                    # fib(0) = 0
  return 1 if n == 1                                    # fib(1) = 1
  (memo[n] = dp_fib(n - 1, memo) + dp_fib(n - 2, memo)) # fib(n - 1) と fib(n - 2) を計算し、メモに入れ、返す
end

因みに、この方法を使っても $n = 10^{18}$ のような場合は流石に時間がかかりすぎます。
そういう場合は行列表現とバイナリー法を組み合わせたり（行列累乗と呼ばれます）、きたまさ法という方法を使って $n$ の対数に比例する時間で計算します。
競技プログラミングでは行列累乗を使う問題もよく出題されることがあります。

GCD (最大公約数)

最大公約数が何かについては小学校で習ったと思うので、詳細には立ち入りません。

ユークリッドの互除法は、 $2$ つの数の最大公約数を計算するシンプルかつ効率的なアルゴリズムで、内容は以下のとおりです。

片方が $0$ なら他方が最大公約数である
片方をもう片方で割ったあまりと置き換え、 1. に戻る

例として、 $10$ と $14$ の最大公約数を計算してみたいと思います。

$$(10, 14) \to (10, 4) \to (2, 4) \to (2, 0) \to 2$$

このように、 $a$ と $b$ の大きい方の対数に比例する計算回数で計算を終えることができます。

「片方をもう片方で割ったあまりと置き換える」という操作において注意するべきは、大きい方で小さい方を割ることを続けるなら、計算が終了しないということです。

そこで以下のコードでは、毎回 2 つの数を入れ替えることで、そうならないようにしています。

関数 gcd(a, b) は $a$ と $b$ の最大公約数を求め、それを返します。

def gcd(a, b)
  return a if b == 0
  gcd(b, a % b)
end

linearSearch (線形探索)

先に説明した二分探索はとても高速ですが、探索する対象がソート済でなければ使えません。
順番に並んでいないものの中から何かを探したいときは線形探索を使うことになります。

たとえば、本から、「う」で終わる二字熟語が最初に現れるのはどこか探したいとします。
どこにその単語があるかは予測できないので、ページを 1 枚 1 枚めくり、すべての行を見て探すと思います。

線形探索はそのように、 1 つ 1 つ確かめる探索です。

長さが $n$ の対象から探すとき、計算回数は、名前のとおり最大で $n$ に比例する回数となります。

関数 linear_search(arr, val) は配列 $arr$ から $val$ を探します。
$arr$ の中に $val$ があるなら、一番左の位置を返します。
もしなければ、 nil を返します。

def linear_search(arr, val)
  len = arr.size              # arr の長さ
  len.times do |i|            # i = 0 から len - 1 まで繰り返す
    return i if arr[i] == val   # arr[i] が val だったら i を返す
  end
  nil                         # false を返す
end

bfs (幅優先探索)

木構造と呼ばれるデータ構造があります。

木構造では、一つのオブジェクトが一つの値を持ち、また、 0 個以上の「子供」のオブジェクトを持ちます。
木構造においてこのようなオブジェクトはノードと呼ばれます。

木構造の例として、 DOM があります。
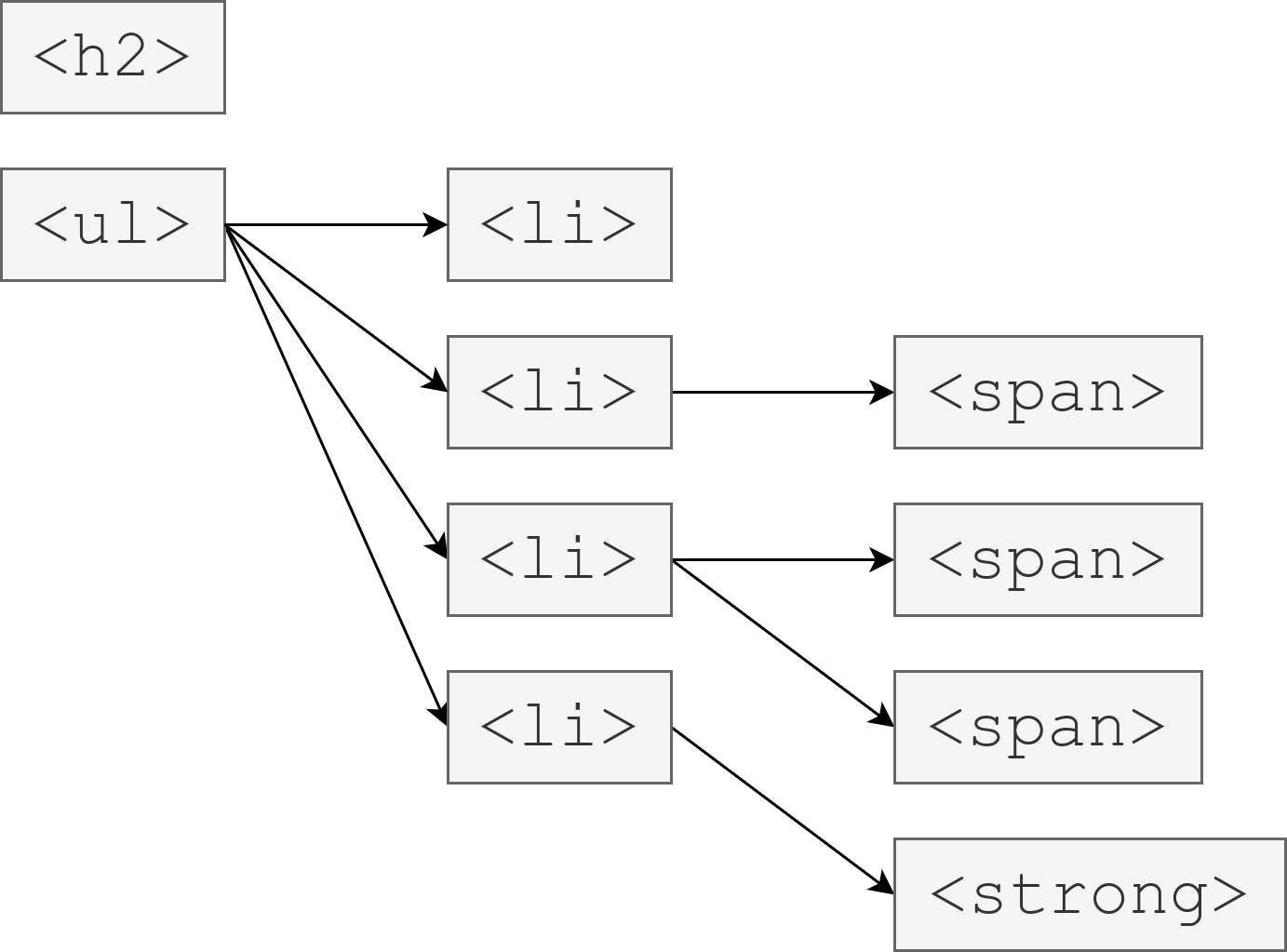
HTML に触ったことがある人ならおそらくわかるでしょうが、 HTML 文書は要素の木構造で表すことができます。この構造は DOM (Document Object Model) と呼ばれ、これによりプログラムから文書を操作するのが容易になります。

HTML	構造	表示

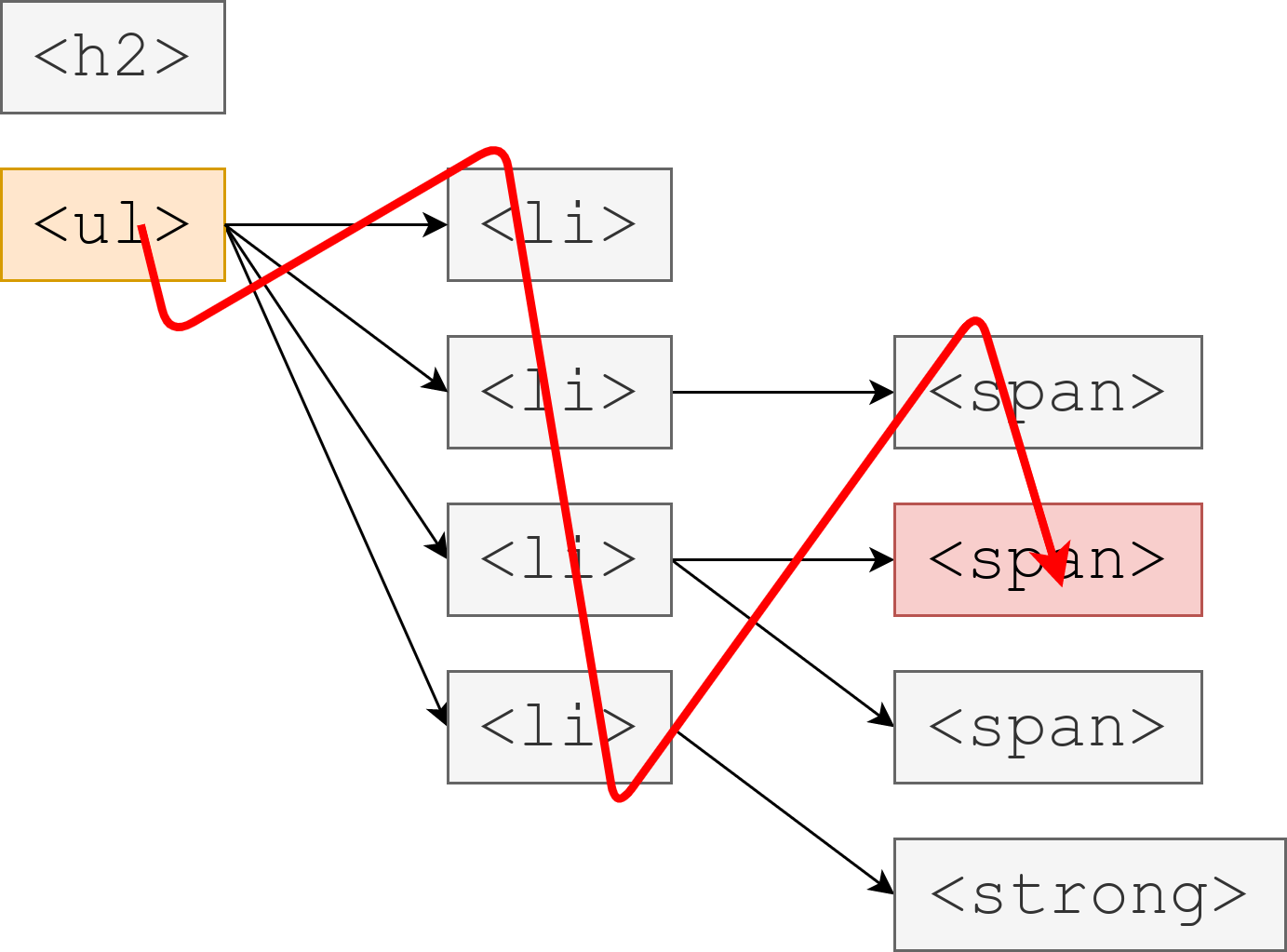
幅優先探索は、そのような木構造を、根（一番左）に近い順に調べていく探索です。

下の図は <ul> を根とする木に対して、 <span style="color:red">400</span> を探す幅優先探索を行った図です。

関数 bfs(root, val) は $root$ を根とする木から、値が $val$ であるようなノードを探し、あればそのノード、なければ nil を返します。

def bfs(root, val)
  queue = [root]                      # root が入ったキュー queue を作る
  until queue.empty?                  # queue が空になるまで繰り返す
    current = queue.shift               # queue の先頭の要素を取り出す
    return current if current.val == val  # 見つけた
    current.children.each do |child|    # current のそれぞれの子に対して繰り返す
      queue << child                      # queue の末尾に child を追加
    end
  end
  nil                              # 見つからなかった
end

余談ですが、 Ruby の実装の一つである CRuby では、配列は Deque として実装されているため、 push (<<), pop だけでなく shift, unshift も定数時間で行うことができます。
しかし、 JavaScript では Array#shift の計算回数は配列の長さに比例するはずですが……。

ZONeエナジープログラミングコンテスト “HELLO SPACE”

mad_hacker の発売を記念してプログラミングコンテストが開かれました。
05/17まで開催されています。

賞金総額は70万円！

これは楽しそうですね！

プログラミングをあまりやったことがない方、または普段プログラミングコンテストなどに出たことがない方などもこの機会に一度参加してみてはいかがでしょう？

著作権があるので、そのまま掲載はできません ↩
隠れている場所は想像で補いました。コーディング規約にあわせて適宜書き換えた場所もあります。また、不要となったため省略した変数もあります ↩
https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A3%E3%83%9C%E3%83%8A%E3%83%83%E3%83%81%E6%95%B0#%E3%81%9D%E3%81%AE%E4%BB%96%E3%81%AE%E8%A9%B1%E9%A1%8C ↩
https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A3%E3%83%9C%E3%83%8A%E3%83%83%E3%83%81%E6%95%B0#%E4%B8%80%E8%88%AC%E9%A0%85 ↩

ZONe mad_hacker にデザインされたプログラムを解説してみた