MojaCoder で人生初のコンテストを開いたので、感想を書きます。
ネタバレ注意です。
Magurofly Beginner Contest 001
コンテストをしてみたかったので用意していた1問に加え2日で5問作って開催しました。キツかった。
今度からは時間に余裕を持ってやろうと思います。
あと、トップページにはペナルティが何分や配点などの情報、Clar先(重要)は書くべきだった。
案の定というか(当時は予想していなかったんですけど)いくつかClarが来て問題の不備が発覚し、アナウンスをする必要がありました。
(アナウンスといっても問題に追記してその旨をツイートするだけですが)
#1 Hastur's Broadcast
First Accepted: chinerist さん
RSA暗号を題材にした問題作ってみたいなーと思っていて、Hastad's Broadcastがあったのでこれを使いました。
$e$乗根を求める問題にしなかったのは、そうするといろいろ制約を増やす必要があると思いそれをしたくなかったからです。
問題
$m \equiv c_1 \mod n_1$
$m \equiv c_2 \mod n_2$
$m \equiv c_3 \mod n_3$
となる最小の正の整数 $m$ を求めよ。
解法
全探索 or 中国剰余定理です。
正の整数というのがわかりにくかったのか、ペナを出している人がたくさんいました。
半分わざとです。ごめんなさい。
#2 Bit Equation
First Accepted: sansen さん
年齢算を$(\mathbb{N}, \oplus, \&)$でやったらどうなるかという興味本位でした。
ストーリーだけ書いたのでちょっとわかりにくかった?
問題
$A = C \& (Y \oplus X \oplus A)$となる最小の非負整数$Y$を求めよ。
解法
ビット毎に全探索 or $C \& (A \oplus (C \& (A \oplus X)))$ です。
#3, #6 Dungeon Attack (Easy, Hard)
First Accepted: どちらも sansen さん
行列累乗を$(\mathbb{Z}, \max, +)$でやるやつあんまり見ないなと思ったので出しました。
問題数水増しのために行列累乗部分を外してEasyを作りました。
Easyは行列累乗では解けないようにしてもよかったかもしれません。貼るだけだと面白くないので。
スタートとゴールの場所が書いていないというとんでもないミスをやらかしてしまいました。
他にも文章力が足りず、いろいろ不明瞭なところがあったので反省です。(例:ゴールに着いても制限時間内であれば他の地点へ行ける、一つの地点で時間を潰すことができる、など)
問題
$N$ 頂点 $M$ 辺のグラフで、頂点 $1$ から頂点 $N$ への辺の本数が $T$ 以下となるパスのうち重みの総和が最大となるものを求め、重みの総和を出力せよ。
解法 #3
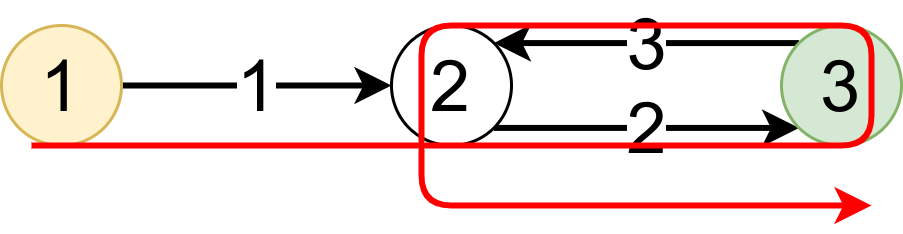
まずサンプル 1 を図示してみます。
正解となる通り方をするとこうなります。
このように、辺を何度も通ることでスコアを稼ぐことができます。
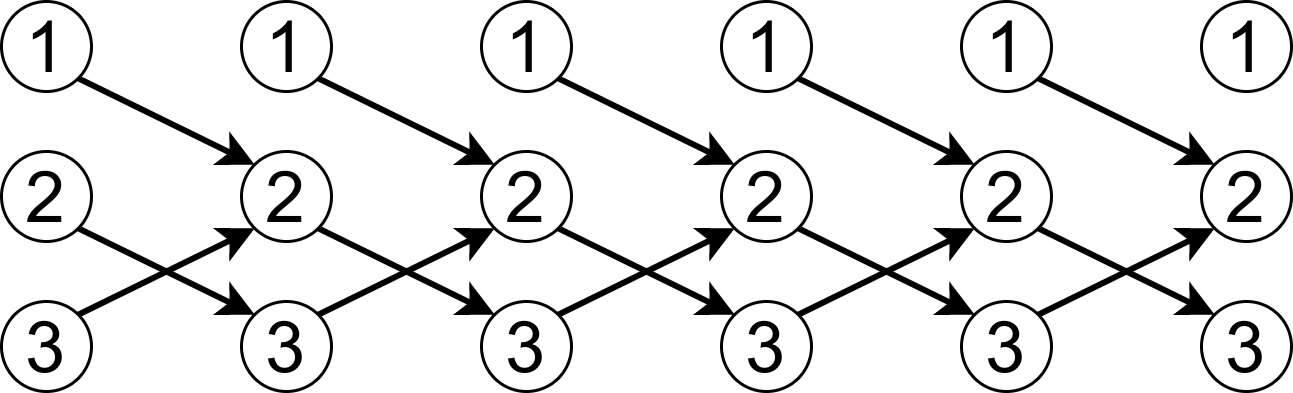
$T, N$ が $T, N \le 100$ と小さいので、時刻 $t$ が $0, 1, 2, \ldots, T$ のとき、それぞれの頂点 $v$ における最大スコアを求めることを考えてみましょう。
DPの表は以下のようになります。
| $t$ \ $v$ | 1 | 2 | 3 |
|---|---|---|---|
| $0$ | $0$ | $-\infty$ | $-\infty$ |
| $1$ | $0$ | $1$ | $-\infty$ |
| $2$ | $0$ | $1$ | $3$ |
| $3$ | $0$ | $6$ | $3$ |
| $4$ | $0$ | $6$ | $8$ |
| $5$ | $0$ | $11$ | $8$ |
$t = 5$ のとき、頂点 $3$ の最大スコアは $8$ です。
$t = i$ のとき $t = i + 1$ のときの各頂点のスコアは $O(N^2)$ で計算できるため、全体で $O(TN^2)$ で解くことができました。
解法 #5
上のような DP の遷移は行列として表すことができ、行列累乗によって解くことができます。
このとき、通常の行列とは違い、和を $\max$ 、積を $+$ として定義します。これは半環になるため行列の形で計算できます。
時刻 $t$ のときの頂点 $v$ のスコアを $S_{tv}$ とすると、遷移行列 $A$ を使って次のように表すことができます。
$$ \begin{bmatrix} S_{t1} \\ S_{t2} \\ \vdots \\ S_{tN} \end{bmatrix} = A^t \begin{bmatrix} S_{01} \\ S_{02} \\ \vdots \\ S_{0N} \end{bmatrix} $$
先程のテーブルの一番上と同じように、
$S_{01} = 1$
$S_{0v} = -\infty \quad (2 \le v \le N)$
となります。
遷移行列 $A$ は以下のように定義されます。
$A_{ii} = 0$ : これは時間が経った時同じ頂点にとどまってもいいからです。
$A_{B_i A_i} = C_i$ : これは辺によるの移動です。
答えは $S_{TN}$ となるため、 $O(N^3 \log T)$ で解くことができました。
……行列累乗するには少し $N$ が大きすぎたので、反省です。
#4 ASCII Squares
First Accepted: chinerist さん
いもす法×文字列がやりたかったので作りました。
当日の典型90問に爆破されるとは思わなかった。
問題
$N$ 個の長方形が与えられる。 $H\times W$ 文字の描画領域に長方形を描画せよ。
解法
いもす法を使い、値が $1$ 以上になるマスを塗ります。
#5 As Soon As Possible 2
First Accepted: chinerist さん
逆方向からダイクストラをするのがやりたかったので作りました。
制約違反があったので、ごめんなさい。
問題
$N$ 頂点 $M$ 辺の強連結なグラフが与えられる。うち $Q$ 個の頂点に対し、その頂点から頂点 $1$ へ行き戻ってくるような最短パスの長さを出力せよ。
解法
順方向と逆方向にダイクストラをして足します。
サイクルを列挙みたいな方法もあったりしませんか?わからないですが
全体の反省
いくら短時間で作ったとしても、ミスだらけで参加者が困ってしまうようではいただけませんね。
問題を増やすよりも問題の見直しをするべきでした。
今度はもっと十分に推敲・テストをして作ります。