tl;nr
異常検知の問題で, 2-out-of-3ロジックを, 3つ以上の検出器を用い, 且つ各検出器の異常検出効率, 誤検知率がばらばらの場合に拡張します. N個の検出器を用い, 最適なMを決めてM個以上で異常を検出した場合に全体として異常と判定するM-out-of-Nロジックと, 各検出器の判定結果から異常/正常の尤度を求めて, 尤度の大きい方の結果を最終的な判定結果とする尤度法の2つの方法について, pythonで計算し, 性能を見ていきます.
はじめに
初めての投稿です. 宜しくお願いします. 異常検知の問題で, 一つの事象を複数回観測しした結果をどう組み合わせれば全体としての検出能力, すなわち異常を正しく検出できる確率(検出効率)と正常を誤って異常としてしまう確率(誤検知率)を最適化できるかを考えます. ここでは, 正常/異常の二つの状態から, 測定によりどちらであるかを判定することを考え, 検出器の検出効率と誤検知率は既知であるとします.
2-out-of-3ロジック
同じ効率を持つ3つの検出器を用意した場合は, 3つの測定結果が得られますが, その多数決, つまり3つのうち2つ以上で得られた結果を最終結果とすることにより, 個々の検出器より検出効率, 誤検知率を向上できます. 各検出器に対して, 検出効率の代わりに, とり逃し確率(不感率)を$\bar{\epsilon}=1-\epsilon$ ($\epsilonは検出効率$), 正常を誤って異常と判定してしまう誤検知率を$f$とします. 2-out-of-3ロジックでの不感率, 後検知率はそれぞれ$\bar{E}$, $F$とすると,
\bar{E} = \Sigma_{m=0}^{1} {}_{m}\mathrm{C}_{3} (1-\bar{\epsilon})^{m} \bar{\epsilon}^{3-m} = -2\bar{\epsilon}^{3} + 3\bar{\epsilon}^{2} \tag{1}
F = \Sigma_{m=2}^{3} {}_{m}\mathrm{C}_{3} f^{m} (1-f)^{3-m} = -2f^{3} + 3f^{2} \tag{2}
と計算できます. どちらも同じ形の式なので, 誤検知率$F$について, 元の値$f$に比べてどれだけ小さくなるかを計算すると,
\frac{F}{f} = -2f^{2} + 3f = -2(f-\frac{3}{4})^{2}+\frac{9}{8} \tag{3}
となります. これを両対数グラフで描くと以下の図の黒色のグラフのようになります:
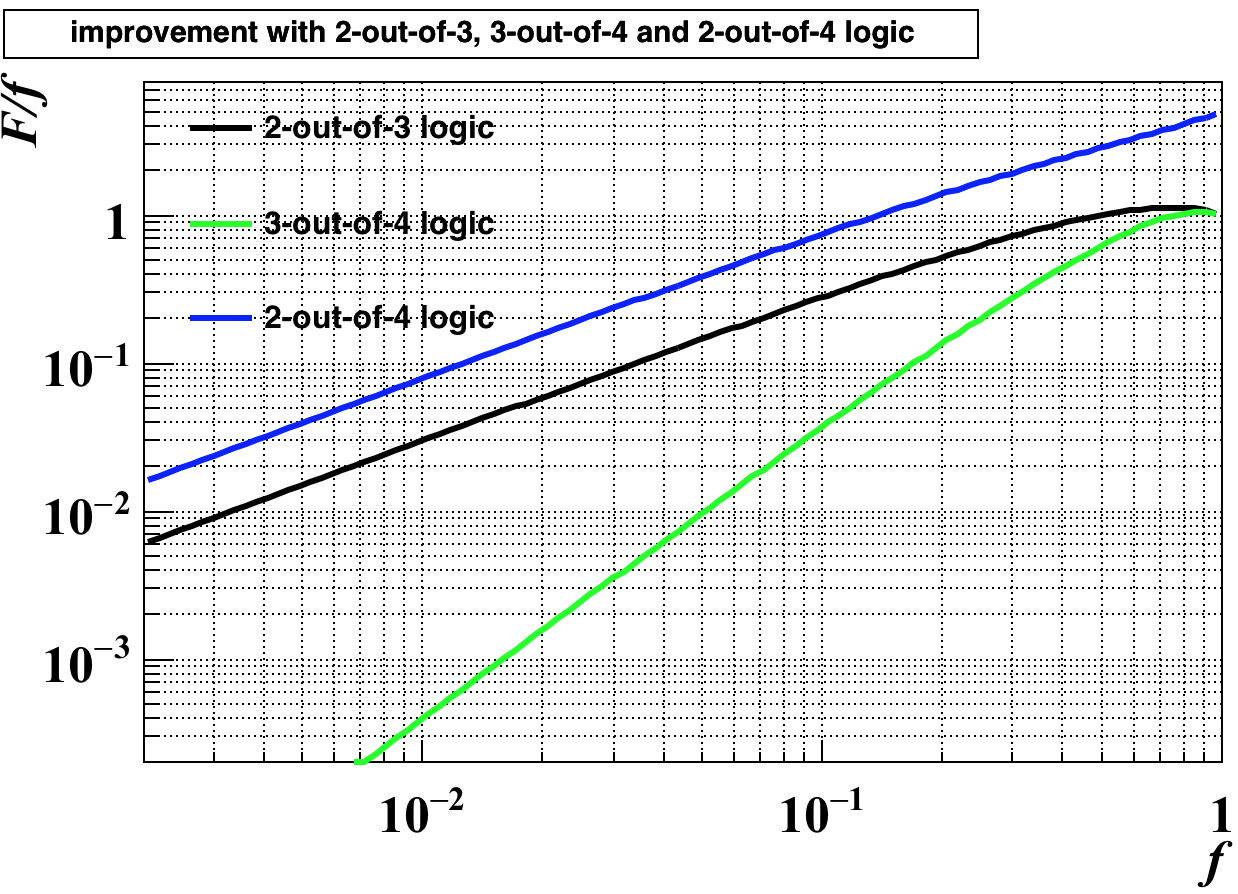
グラフはC++のデータ解析ライブラリROOTを用いて描いています. 1 元の誤検知率(または不感率)が50%以下であれば, 2-out-of-3ロジックを使うことで, 誤検知率(または不感率)を小さくできます. また, 元の数値が小さいほど相対的な改善度合いも大きく, 例えば$f=0.2$だと, $F/f=0.52$と, およそ元の半分になり, $f=0.05$だと$F/f=0.145$と一桁近く小さくなります.
M-out-of-Nロジック (同じ検出能力の場合)
前節の式(1),(2)の2, 3のところにそれぞれ$M$, $N$に置き換えると検出器が多数ある場合にも一般化できます. $N$が奇数の場合は, $M=(N+1)/2$とすると, 全体としての不感率, 後検知率は元の値より同じだけ向上します. $M>(N+1)/2$だと誤検知率, 不等号の向きが逆だと不感率をそれぞれ重視した判定になります. 例えば$N=4$であれば, $M=3, 2$の時の誤検知率はそれぞれ先の図の緑, 青色のグラフのようになり, 不感率はそれぞれもう一方の色のグラフのようになります.
一般化M-out-of-Nロジック
個々の検出効率がバラバラな場合は, それらをどう組み合わせれば最適な判定となるかは個々の検出能力によるため, 一般的に示すことは難しいと思われます. そこで, 事前に知っている$N$個の各検出器の検出能力の値から, 最適な$M$の値を予め決めておき, 運用時はその$M$個以上で異常判定を得た場合に全体として異常を検出したことにします. 全体としての検出性能の式を書き下すことはできますが, 変数が多くなり全体の傾向を見るのの適切ではないと思われるので, pythonで計算することにします.
- 一般的に各検出器は, 閾値を調整することで不感率, 誤検知率を調整することができますので, ここでは不感率は検出器毎で共通の値とし, 誤検知率だけがバラバラの値を考えます.
- 「最適な」$M$を決める際の指標はいろいろあり得ますが, ここでは文献[1]に従って, 異常サンプル, 正常サンプルそれぞれの検出効率($1-\bar{E}$, $1-F$)の調和平均(F値)を用います. およそですがFP, FNがバランスして小さくなるほど良いと判定します.
- (3)式にあるように, 例えば誤検知率が大きすぎると, 判定結果を足し合わせても誤検知率は小さくならない場合が有ります. 従って, 誤検知率が大きい順に検出器を省き, $N-1$個, $N-2$個, ...の場合も考慮し, F値を比較して最適な条件を選びます.
コード
githubにアップしました. 組み合わせの計算を行う必要がありますが, itertoolsのライブラリを使うと与えたリストに対して全てのパターンを出力してくれるので便利です.
pythonでの計算例
5つの検出器があり, 不感率$\bar{\epsilon}$は全て0.01, 誤検知率がそれぞれ0.01, 0.02, 0.1, 0.3, 0.5だったとします. 一般化M-out-of-Nロジックでの性能は,
python findBestDetCombi.py -p 0.01 0.02 0.1 0.3 0.5
input false positive rates : [0.01, 0.02, 0.1, 0.3, 0.5]
input false negative rate : 0.01 (common for all the detectors)
****M-out-of-N logic****
(4, 5) : (0.0004840000000000001, 0.0009801495999999998, 0.9992678636138077)
(3, 4) : (0.0009620000000000002, 0.00059203, 0.99922295075394)
(2, 3) : (0.0031600000000000005, 0.00029800000000000003, 0.9982689486922889)
best condition : N = 5, M = 4, FP = 0.0004840000000000001, FN = 0.0009801495999999998
のようになり, 5つともの検出器を使って, $M=4$個以上の検出器で以上判定された場合に全体として異常判定とするのが最も性能が良いようです. 50%も誤検知率があってもこの場合は含めたほうが全体としての性能は良いということになります. 最後の検出器の誤検知率が70%とすると, $N=4$, $M=3$がベストとなり, 最後の検出器は含めないほうが良いという結果になります.
もう少し性能の悪いものばかりを組み合わせた場合はどうでしょうか? 例えば, 0.1, 0.2, 0.3, 0.4, 0.5の5つだと,
(4, 5) : (0.027899999999999998, 0.0009801495999999998, 0.9853761011810264)
(3, 4) : (0.0522, 0.00059203, 0.9729200871810318)
(2, 3) : (0.11699999999999999, 0.00029800000000000003, 0.9377340290709841)
best condition : N = 5, M = 4, FP = 0.027899999999999998, FN = 0.0009801495999999998
4-out-of-5とすることで, 誤検知率は3%程度にまで下がっています.
尤度を用いる方法
上記の方法は, 個々の判定結果の個数を数えているだけで, 明示的に性能の高い検出器($\bar{\epsilon}$,$f$が小さい)の決定を重視するようなことはしていないので, 情報を使い切っていないような気がします. 安直に考えると, 各検出器の判定結果に対して, 性能が高いものに高い重みをかけた上で足し合わせれば良いと思われます. その「重み」に対応するものとして, 異常状態と正常状態をそれぞれ仮定した時の負の対数尤度(Negative Log Likelihood, NLL)を計算し, NLLが小さい(尤度が大きい)仮定を最終結果として採用します.
具体的に式で書くと, $N$個の検出器の不感率と誤検知率をそれぞれ$\bar{\epsilon_{1}}$,$\bar{\epsilon_{2}}$,...,$\bar{\epsilon_{N}}$,$f_{1}$,$f_{2}$,...,$f_{N}$, 観測結果を$y_{1}$, $y_{2}$,...,$y_{N}$ ($y_{i}=0,1$;1の時に異常を検出したとする)としたとき, 異常を仮定した時にこの結果が得られる負の対数尤度$L_{1}$は
L_{1} = -\Sigma_{n=1}^{N} (y_{i}\log(1-\bar{\epsilon_{i}})+(1-y_{i})\log\bar{\epsilon_{i}})
となり同様に, 正常状態を仮定した時の尤度$L_{0}$は
L_{0} = -\Sigma_{n=1}^{N} (y_{i}\log f_{i}+(1-y_{i})\log(1-f_{i}))
となります. この両者を比較して, $L_{1}>L_{0}$であれば異常, 逆であれば正常と評価します.
pythonでの計算例
先程の$M$-out-of-$N$ロジックのコードでのクラスに, 別のメソッドとしてこの方法による判定を計算するコードを実装しました. 検出能力の期待値を計算するのに, $N$個の検出器での全ての検出パターンを網羅して, それぞれ発生確率と尤度を計算して正しく判定されない確率を足し合わせて評価します. 全てのパターンを書き出すのに, range(2**N)でforループを回し, それぞれを二進数表記することで全パターンを取得しています. (何かライブラリがありそうですが...)
先程と同様に, 不感率$\bar{\epsilon}$を0.01, 誤検知率を0.01, 0.02, 0.1, 0.3, 0.5とすると, 計算結果は
(0, 5) : (0.000581, 0.0006890599, 0.9993649671289094)
(0, 4) : (0.0009620000000000002, 0.00059203, 0.99922295075394)
(0, 3) : (0.0031600000000000005, 0.00029800000000000003, 0.9982689486922889)
(0, 2) : (0.01, 0.01, 0.99)
best condition : N = 5, FP = 0.000581, FN = 0.0006890599
となり, 5つとも使ったほうが良いという結果になります. 最後の検出器の誤検知率を0.7にすると, 先程のM-out-of-Nロジックとは少し違う結果を返します:
(0, 5) : (0.0008720000000000002, 0.00059203, 0.9992679653898449)
(0, 4) : (0.0009620000000000002, 0.00059203, 0.99922295075394)
(0, 3) : (0.0031600000000000005, 0.00029800000000000003, 0.9982689486922889)
(0, 2) : (0.01, 0.01, 0.99)
best condition : N = 5, FP = 0.0008720000000000002, FN = 0.00059203
誤検知率が大きい場合, M-out-of-Nで試した, (0.1, 0.2, 0.3, 0.4, 0.5)やは, この方法では性能の改善が見込めないようで, 一番後検知率のよいもの一つだけで判定した方がマシということになりました.
結局どちらの方法がいいのか
すでに上記で同じ誤検知率で両方のアルゴリズムを試していますが, M-out-of-Nの方が少々性能がよいようです. 元の目論見では, 尤度を使ったほうが性能が出ると思っていましたが...
参考文献
-
筆者がpythonのmatplotlibに精通していないだけ. ↩