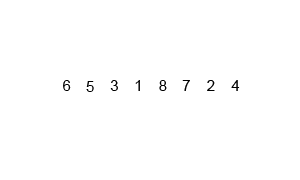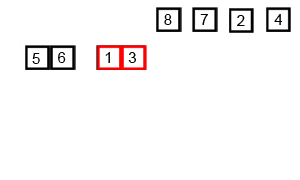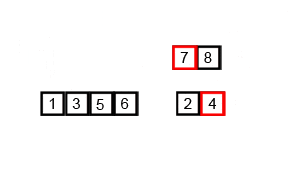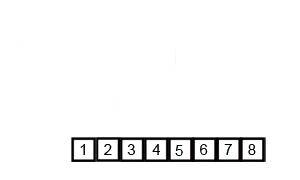基本的なソートアルゴリズムとPythonによる実装例

概要

基本的なソートアルゴリズムの概要と、Pythonによる実装例をまとめました。　

挿入ソート（Insertion Sort）

概要

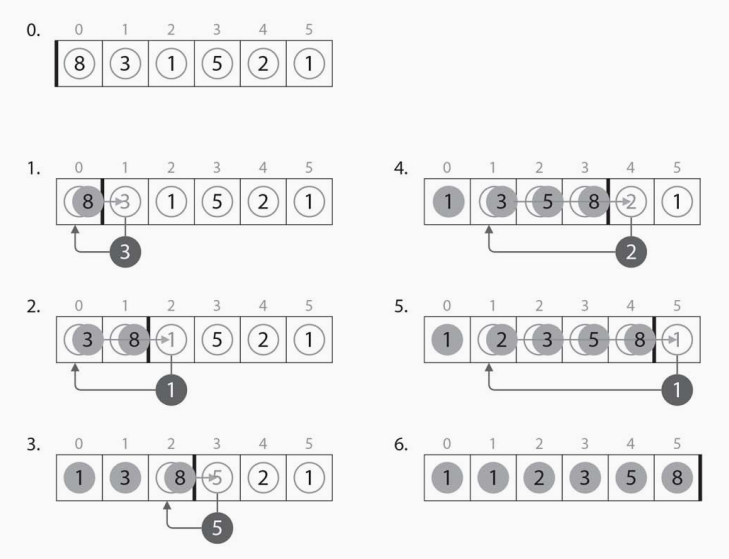
挿入ソートは手に持ったトランプの並べ替え方に例えられる手法です。配列をソート済みの部分と未ソートの部分に分けて考え、未ソート部分の要素をソート部分の然るべき位置に挿入していくイメージです。平均計算時間・最悪計算時間はともにO($n^2$)ですが、ある程度整列されたデータに対しては高速に動作します。安定(stable)なソートアルゴリズムです。

実装例

# 配列aを挿入ソートで昇順に並べ替える
def insertion_sort(a):
    for i in range(len(a) - 1):
        # a[i]の一つ右の要素: a[j]をソート対象に定める
        j = i + 1

        # a[j]がソート済みの位置に収まるまで繰り返す
        while i >= 0:
            # a[j]を一つ左の要素と比較し、a[j]の方が小さければ交換する
            if a[j] < a[i]:
                a[i], a[j] = a[j], a[i]
                # 比較対象が左に移動しているので、indexを1ずつ減らす
                i -= 1
                j -= 1
            else:
                break

参考

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=ALDS1_1_A
https://ja.wikipedia.org/wiki/挿入ソート

バブルソート（Bubble Sort）

概要

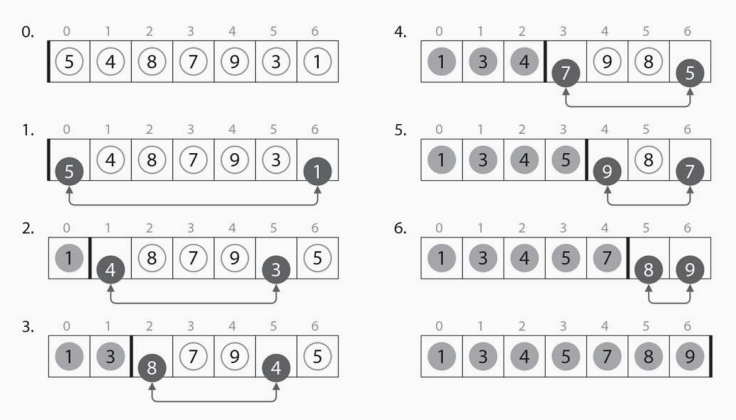
バブルソートは隣り合う要素で大小が逆になっているものを交換していく手法です。下図のように列の末尾から要素の交換を行っていく場合、列の先頭から順にソートされていくイメージです。バブルソートで整列するのに必要となる要素の交換回数は反転数（転倒数）と呼ばれ、列の乱れ具合を表す数値として用いられます。平均計算時間、最悪計算時間はともにO($n^2$)で、安定(stable)なソートアルゴリズムです。

実装例

※上の図とは逆に、列の先頭から末尾に向かって要素の交換を行なっていきます

# 要素数2以上の配列aを昇順にソートする
def bubble_sort(a):
    # (要素数−1)回繰り返す
    for i in range(len(a) - 1):
        # 列の先頭2要素を最初の比較対象に選ぶ
        l = 0
        r = 1

        # rが末尾に達するまで、隣り合う要素の大小を比較する
        while r < len(a):
            # 隣り合う要素の大小が逆であれば交換する
            if a[l] > a[r]:
                a[l], a[r] = a[r], a[l]
            # 比較対象のindexをインクリメントする
            l += 1
            r += 1

参考

https://ja.wikipedia.org/wiki/バブルソート
http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=ALDS1_2_A

選択ソート（Selection Sort）

概要

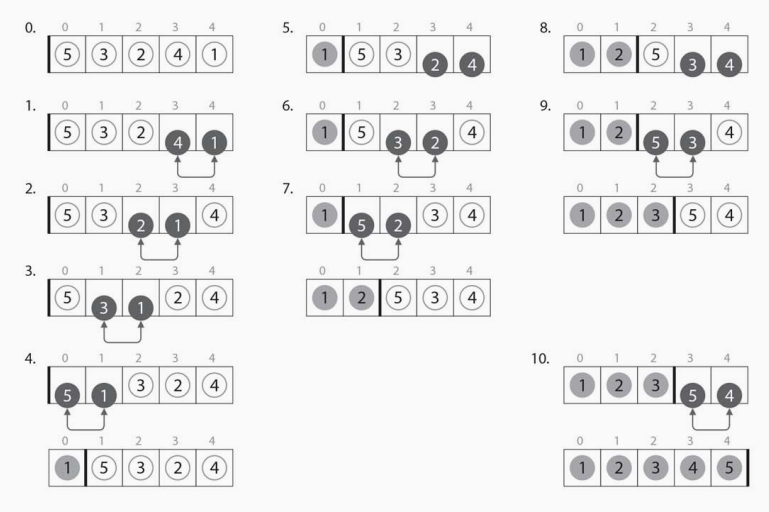
選択ソートは最小値を逐次探していき、未ソート部分の先頭に移動していくことで整列を行う手法です。平均計算時間、最悪計算時間はともにO($n^2$)で、不安定(unstable)なソートアルゴリズムです。

実装例

# 配列aを昇順にソートする
def selection_sort(a):
    for i in range(len(a)):
        # 最小値のindex
        min_idx = i

        # i以降の要素で最小のものを探す
        for j in range(i + 1, len(a)):
            if a[j] < a[min_idx]:
                min_idx = j

        # 発見した最小値を未ソート部分の先頭に移す
        if i != min_idx:
            a[i], a[min_idx] = a[min_idx], a[i]

参考

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=ALDS1_2_B
https://ja.wikipedia.org/wiki/選択ソート

マージソート（Merge Sort）

概要

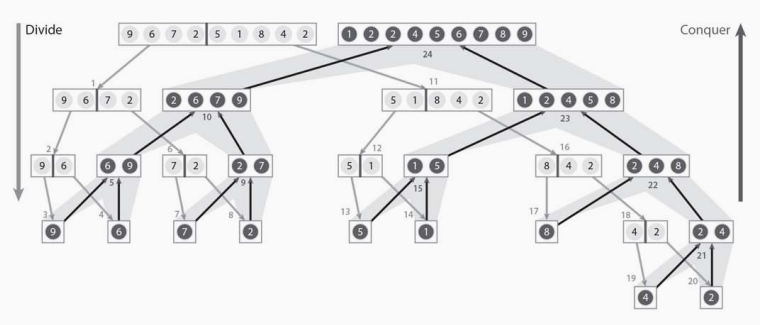
マージソートは分割統治法（Divide and Conquer）を用いて整列を行う手法です。対象となる配列を一つの要素になるまで分割し、大小関係を比較しながらマージを行うことで、最終的に整列された配列を得ることができます。n個の要素を持つ配列の分割に必要となる計算量は$O(logn)$、マージに必要となる計算量は$O(n)$となるため、マージソートの計算量は$O(nlogn)$となります。安定(stable)なソートアルゴリズムですが、一時的な作業記憶領域を必要とする場合があります。

実装例

# 配列aを昇順に並べ替える
def merge_sort(a):
    if len(a) == 1:
        return

    # 配列を二つに分ける
    m = len(a) // 2
    x = a[:m]
    y = a[m:]

    # 分割とマージを再帰的に行う。最終的に一つの要素まで分割された段階からマージが行われていく
    merge_sort(x)
    merge_sort(y)
    merge(x, y, a)

# 配列x, yをマージし、aにセットする
def merge(x, y, a):
    # x, yのindex
    i = 0
    j = 0

    # x, yの先頭の要素を比較し、小さい要素から順にaにセットしていく
    while i < len(x) or j < len(y):
        # xの要素を全て追加済みの場合、y[j]をセットする
        if i == len(x):
            a[i+j] = y[j]
            j += 1
        # yの要素を全て追加済みの場合、x[i]をセットする
        elif j == len(y):
            a[i+j] = x[i]
            i += 1
        # x[i]がy[j]以下の場合、x[i]をセットする
        elif x[i] <= y[j]:
            a[i+j] = x[i]
            i += 1
        # y[j]がx[i]より小さい場合、y[j]をセットする
        else:
            a[i+j] = y[j]
            j += 1

参考

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=ALDS1_5_B&lang=en
https://ja.wikipedia.org/wiki/マージソート

その他（追加予定）

• シェルソート
• クイックソート
• ヒープソート
• 基数ソート
• バケツソート