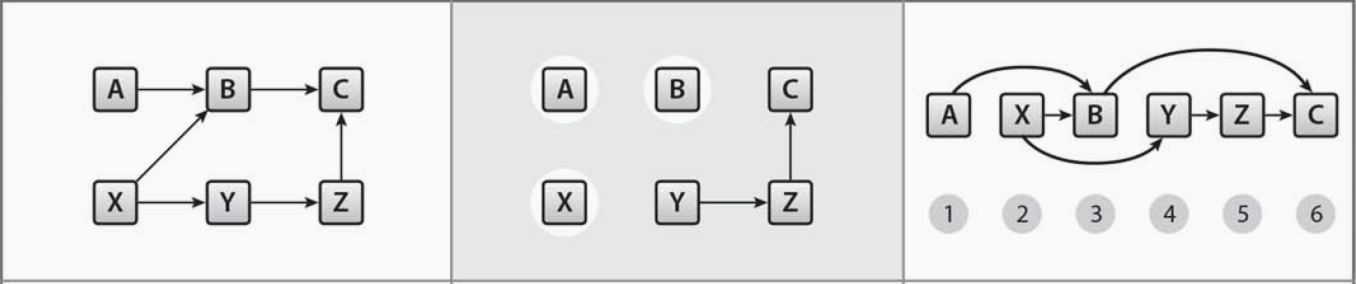
有向非巡回グラフ（DAG）とトポロジカルソート

有向非巡回グラフ（DAG）

有向非巡回グラフ（Directed Acyclic Graph: DAG）とは、閉路のない有向グラフのことである。サイクルが存在しないため、ある頂点から同じ頂点に戻ってこれないという特徴がある。

有向非巡回グラフは要素の因果関係や物事の依存関係をモデル化するのに有効である。例えばあるタスクを行う前に別のタスクを完了させておく必要がある場合、タスクを頂点、順序の制約を有向辺とみなすと、各タスクの依存関係を有向非巡回グラフで表現することができる。また後述するトポロジカルソートを使用することで、制約条件に従ってタスクを完了させるための適当な順序を得ることができる。ただしジャンケンのグー・チョキ・パーのように依存関係（強さの順序）がサイクルを形成するような場合、巡回グラフとなるため順序付け（トポロジカルソート）を行うことはできない。

トポロジカルソート

トポロジカルソート（Topological sort）は、有向非巡回グラフ（DAG）の各ノードを順序付けして、各ノードをその出力辺の先のノードより前にくるように並べることである。グラフがトポロジカルソート可能であることは、そのグラフが有向非巡回グラフであることと等価である。トポロジカルソートの活用例としては、Job scheduling、論理合成、Makefile等でのファイルのコンパイル順序の決定、リンカのシンボル依存関係の解決などが挙げられる。

例題 1

prerequisites[i] = [A, B]が与えられたとき、コースAを受講するには事前にコースBを受講しなければならないとします。例えば[0, 1]のペアは、コース0を受講するためには、まずコース1を受講しなければならないことを示しています。与えられた制約条件に従って全てのコースを終了することが可能な場合はtrueを、不可能な場合はfalseを返してください。

出典：https://leetcode.com/problems/course-schedule/

考察

この問題は一種のグラフ探索問題としてモデル化することができます。ここでは各コースをグラフの頂点とみなし、コース間の依存関係を2つの頂点間の有向エッジとしてモデル化します。そして、すべての依存関係（制約条件）を満たす有効なコースのスケジュールを構築できるかどうかを判断するということは、対応するグラフがDAG（Directed Acyclic Graph）であるかどうか、つまりグラフにサイクルが存在しないかどうかを判断することと等価です。

グラフ探索問題の典型的な戦略に、DFS（深さ優先探索）の一種であるバックトラックがあります。バックトラックは制約充足問題を解くのによく使われる一般的なアルゴリズムで、解の候補を段階的に構築し、その候補が有効な解をもたらさないと判断した時点で候補を放棄する（バックトラックする）というものです。

各コースの環状依存性のチェックは、バックトラックによって行うことができます。ここでは、受講可能なコースがなくなるか、以前受講したはずのコースが再び現れる（サイクルを検出する）まで、グラフを段階的に探索していきます。

実装例

from collections import defaultdict

class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: bool
        """

        def hasCycle(node, visited):
            """
            :param node: 現在訪れているノード
            :param visited: 過去に訪れたノードの集合
            :return: bool (閉路が存在するか否か)
            """
            # すでに保存された結果があればそれを返す
            if node in checked:
                return checked[node]

            # すでに訪れたnodeに再会（閉路を検出）
            if node in visited:
                return True
            else:
                visited.add(node)

            result = False

            # 隣接するノードに対して再帰的に探索を行う
            for adj in g[node]:
                if hasCycle(adj, visited):
                    result = True
                    break

            checked[node] = result
            return checked[node]

        g = defaultdict(list)
        checked = {}  # 効率化のため、結果を保存しておく

        # 有向グラフ（隣接リスト）を生成
        for course in prerequisites:
            a, b = course[0], course[1]
            g[b].append(a)

        # グラフの各頂点から探索を開始し、閉路が存在するかどうか調べる
        for node in list(g):
            if hasCycle(node, set()):
                return False

        return True

補足

アルゴリズムの全体的な構造は、以下の3つのステップで構成されています。

Step 1

与えられたコースの依存関係のリストから、グラフデータ構造を構築します。ここでは、グラフを表現するために隣接リストを採用しています。これはハッシュマップや辞書で実装することができます。隣接リストのkeyは各コースを表し、そのコースを終了後に受講できるコースのリストを値として保持します。

Step 2

次に構築されたグラフの各ノード（コース）を列挙し，そのノードから探索を開始した際に閉路を検出できるかを確認します。

Step 3

以前探索した経路を再度探索するのは無駄なので、動的計画法の要領で結果をcheckedに保存しておき、探索済みの場合はそれを返すようにします。

例題 2

prerequisites[i] = [A, B]が与えられたとき、コースAを受講するには事前にコースBを受講しなければならないとします。例えば[0, 1]のペアは、コース0を受講するためには、まずコース1を受講しなければならないことを示しています。与えられた制約条件を満たしつつ、全てのコースを受講可能な順序を返してください。複数の解が存在する場合は、そのうちのひとつを返すものとします。条件を満たす順序が存在しない場合、空の配列を返してください。

出典: https://leetcode.com/problems/course-schedule-ii/

考察

入力辺（In-degree）を利用したトポロジカルソート

トポロジカルソート順の最初のノードは、入力辺を持たないノードになります。基本的に、入力辺（in-degree）の数が0のノードは、トポロジカルソートされた順序の最初のノードになり得ます。このようなノードが複数ある場合、その相対的な順序は問題にならず、どれから始めても構いません。

まず、in-degreeが0のノード（コース）をすべて受講します。これは、前提条件となるコースがないコースを真っ先に受講することを意味します。次にこれらのコースをグラフから削除し、それらから発生している辺も削除すると、次に処理されるべきコースを見つけることができます。これもまた、入力辺が0のノードです。すべてのコースが処理されるまで、この作業を続けます。

実装例

from collections import deque, defaultdict

class Solution(object):
    def findOrder(self, numCourses, prerequisites):
        # 入力辺、出力辺のそれぞれに対してグラフを用意する
        in_degrees, out_degrees = defaultdict(list), defaultdict(list)
        arr, s = [], set(list(range(numCourses)))
        
        for edge in prerequisites:
            dst, src = edge[0], edge[1]
            out_degrees[src].append(dst)
            in_degrees[dst].append(src)

            # 入力辺を持つノードを除外
            if dst in s:
                s.remove(dst)

        # 入力辺を持たないノードをqに入れる
        q = deque(list(s))

        # 入力辺を持たないノードがなくなるまで繰り返す
        while q:
            node = q.popleft()
            arr.append(node)

            # 隣接ノードを走査
            for adj in list(out_degrees[node]):
                # nodeからの入力辺を削除
                in_degrees[adj].remove(node)

                # 隣接ノードの入力辺の数が0になった場合、qに追加する
                if len(in_degrees[adj]) == 0:
                    q.append(adj)

            # nodeをグラフから削除
            del out_degrees[node]

        # グラフから全てのノードが削除されていればトポロジカルソート完了
        if len(out_degrees) == 0:
            return arr
        # グラフに入力辺を持つノードが残っている場合、閉路が存在する（トポロジカルソート不可）
        else:
            return []

方針

1. 入力辺の数が0のノードをキューに追加
2. キューから先頭ノードを取り出し、ソート順序に追加
3. 先頭ノードの隣接ノードを走査し、先頭ノードからの入力辺を取り除く
4. 隣接ノードが持つ入力辺の数が0になった場合、その隣接ノードをキューに追加
5. 先頭ノードをグラフから削除
6. キューの中身がなくなるまで2~5を繰り返す

上記の操作の完了後、 グラフから全てのノードが取り除かれていればトポロジカルソート成功、グラフにノードが残っていればトポロジカルソート失敗となる。

補足

実装例ではキュー(deque)を用いたが、Stackを用いても構いません。その場合トポロジカルソート順は異なるものになりますが、いずれにせよ制約を満たす順序が得られるはずです。