概要
グラフや木の探索に用いられる幅優先探索と深さ優先探索について、Pythonでの実装を用いながら紹介します。
幅優先探索 (Breadth First Search: BFS)

幅優先探索(BFS)はグラフにおける探索方法の一種で、与えられたnodeから近いnodeを順に探索していきます。深さ優先探索(DFS)ではスタックを用いるのに対し、BFSはキューを使って実装することができます。ノード間の最短距離を求めたい時などに使えます(辺の重みの有無、有向/無向等の性質によって実装が変わってくるので注意)。以下にPythonによる実装の一例を示します。
実装
# Make tree as follows:
# 1
# / \
# 2 3
# / \ / \
# 4 5 6 7
from collections import deque
class Node:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
node1 = Node(1) # Root node
node2 = Node(2)
node3 = Node(3)
node4 = Node(4)
node5 = Node(5)
node6 = Node(6)
node7 = Node(7)
node1.left = node2
node1.right = node3
node2.left = node4
node2.right = node5
node3.left = node6
node3.right = node7
# キューを作成して初期ノード(root)を入れる
q = deque()
q.append(node1)
# キューが空になるまで繰り返す
while len(q) > 0:
# キューの先頭(左端)からnodeを取り出す
node = q.popleft()
if node is not None:
print(node.val)
# nodeの子要素をキューの末尾(右端)に入れる
q.append(node.left)
q.append(node.right)
出力結果
1
2
3
4
5
6
7
深さ優先探索 (Depth First Search: DFS)
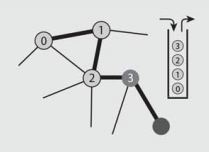
深さ優先探索(DFS)はグラフにおける探索方法の一種で、与えられたnodeから可能な限り遠くまで探索していく手法です。幅優先探索(BFS)ではキューを用いるのに対し、DFSはスタックまたは再帰を使って実装することができます。以下にPythonによる実装の一例を示します。
実装
# Make tree as follows:
# 1
# / \
# 2 5
# / \ / \
# 3 4 6 7
class Node:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
node1 = Node(1)
node2 = Node(2)
node3 = Node(3)
node4 = Node(4)
node5 = Node(5)
node6 = Node(6)
node7 = Node(7)
node1.left = node2
node1.right = node5
node2.left = node3
node2.right = node4
node5.left = node6
node5.right = node7
def traverse(node):
if node is not None:
print(node.val)
# 子要素に対して再帰的に呼び出していく
traverse(node.left)
traverse(node.right)
traverse(node1)
出力結果
1
2
3
4
5
6
7
補足
上記のように木を探索する手法は先行順巡回 (pre-order)とも呼ばれます。他にも中間順巡回 (in-order)、後行順巡回 (post-order)といった手法があるので、気になる方は調べてみてください。