概要
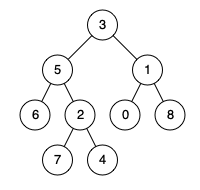
木構造における最小共通祖先(Lowest Common Ancestor: LCA)とは、ある二つのノードが与えられた時、その両方を自身以下に持つノードのうち、最も低い(葉に近い)位置にあるノードのことを指します。一方のノードがもう一方のノードの直接の祖先となっている場合は、直接の祖先となっているノードがLCAとなります。例えば以下の二分木において、6と4のLCAは5、0と1のLCAは1となります。
LCAを探索するアルゴリズムは複数ありますが、本記事では各ノードから自身の祖先を辿っていき、最初に遭遇する共通の祖先を探し出す手法を紹介します。
方針
各ノードから自身の祖先を辿ろうとする場合、各ノードは自身の親を知っていなければなりません。そこで方針としては下記になります。
- 各ノードを巡回し、各ノードの親をdictionaryに保存しておく
- 与えられた二つのノードのうち、一方のノードから親を辿っていき、rootに達するまでに辿ったノード(全ての祖先)をsetに保存しておく
- もう一方のノードから親を辿っていき、2で保存したsetに含まれるノードが現れた時、それが共通の祖先(LCA)となる
注:1では与えられた二つのノードの親が見つかった時点で巡回を打ち切る方が効率的ですが、今回は便宜上全ノードを巡回することにします。
実装例
class TreeNode(object):
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution(object):
# 各ノードをDFSで巡回しつつ、親ノードをdictionaryに保存していく
def traverse(self, node, parents):
if node is None:
return parents
if node.left is not None:
parents[node.left] = node
self.traverse(node.left, parents)
if node.right is not None:
parents[node.right] = node
self.traverse(node.right, parents)
return parents
# ノードp, qのLCAを探索するメソッド
def lowestCommonAncestor(self, root, p, q):
# 各ノードをkey、その親をvalueに持つdictionaryを作成しておく
parents = {root: None}
parents = self.traverse(root, parents)
# 一方のノード(ここではp)の祖先を保存しておくためのsetを用意する
ancestors = set()
# 自分自身がLCAになる可能性もあるため、まずは自身をセットする
parent = p
# pの親を辿っていき、祖先となるノードを全てsetに保存していく
while parent is not None:
ancestors.add(parent)
parent = parents[parent]
# 次にqから親を辿っていき、pの祖先とぶつかった時点でLCAとみなす
node = q
while node not in ancestors:
node = parents[node]
return node