GoogleSpreadSheetでバグ収束予測をするには？

テストフェーズの中盤で、この先、いつ頃バグが収束するのか？、この先何件バグが発生するのか？将来を予測したい時があると思います。

そんな時は、これまで発生したバグの件数を元に、今後どのように成長曲線が引けるかと予測するとよいです。
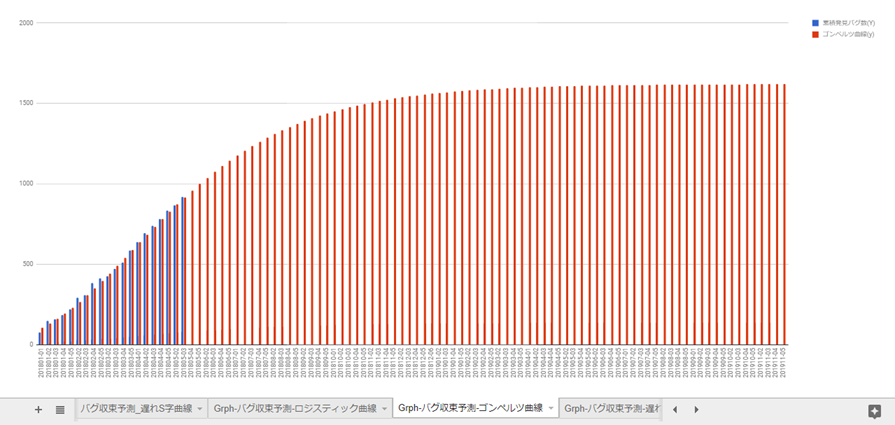
こんな感じです。青棒グラフは実際に発生したバグの累積です。赤棒グラフは予測値です。

今回道具として用いるのは「GoogleSpreadSheet」とそれのアドオンの「Solver」です。
Excelの分析ツールのソルバーでも同じことができるのですが、その辺はググれば出てくるので、ここは敢えて「GoogleSpreadSheet」でやろうかと。

今回使うアドオンの「Solver」ですが、「GoogleSpreadSheet」に登録する際、「Googleドライブファイルの表示と管理」や「外部サービスへの接続」等、いくつか許可を求めてきます。ちょっと気持ち悪いのでサブアカウントで試しました。
下記で試したGoogleSpreadSheetを公開しています。
式を埋めるのが面倒な方は、こちらをコピーして利用してください。
公開リンク:バグ収束予測GoogleSpreadSheet

目次

1. 「GoogleSpreadSheet」にアドオン「Solver」を登録する。
2. 代表的な成長曲線3種類を引いてみる。
   
   2.1.ロジスティック曲線
   
   2.1.1.データと式の設定
   
   2.1.2.「Solver」の実行
   
   2.1.3.グラフ化
   
   2.2.ゴンペルツ曲線
   
   2.3.遅れS字曲線
   
3. バグ実績件数と一番マッチしている成長曲線で将来を予測する。
4. 参考文献

#　ところで、「Solver」って何に使うの？
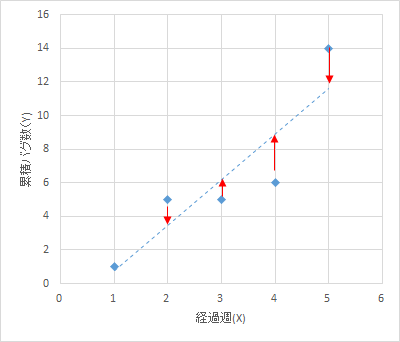
今回は、バグの実績件数(下図の青の点)に、近似曲線(下図の点線)を引くときの、最適な傾き、切片等の関数の最適なパラメータを求めるのに「Solver」を使います。

下図の赤の線の誤差が最小になるように(最小二乗法 - Wikipedia)、傾き、切片をうまいこと算出するツールとして、「Solver」を使います。

1．「GoogleSpreadSheet」にアドオン「Solver」を登録する。

「メニュー」バーの「アドオン」メニューをクリックします。
「メニュー」アイテムから、「アドオンを取得...」をクリックします。

「アドオン」ダイアログが開きます。

右上の「アドオンを検索」テキストボックスに、「Solver」と入力して、「Enter」キーを押して検索します。

検索結果から「Solver」を選び、「＋無料」ボタンをクリックします。
※非線形モデル(non linear)に対応したアドオンを選ぶ必要があります。

「ログイン」ダイアログが表示されますので、自身のアカウントアイコンのあたりをクリックします。

「Solver」がアクセス許可を求めてくるので、「許可」ボタンをクリックします。
ちょっと気持ち悪いです。

アドオンの登録が上手くいくと、このようなツールチップが表示されます。

2. 代表的な成長曲線3種類を引いてみる。

バグ実績は、20週分採取している前提です。

2.1. ロジスティック曲線

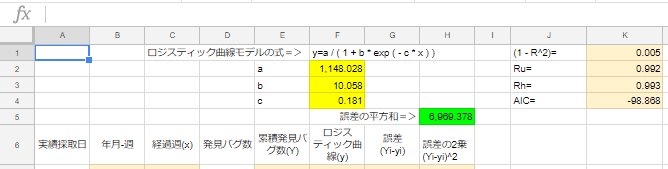
ロジスティック曲線モデルの式＝＞y=a/(1+b*exp(-c*x)

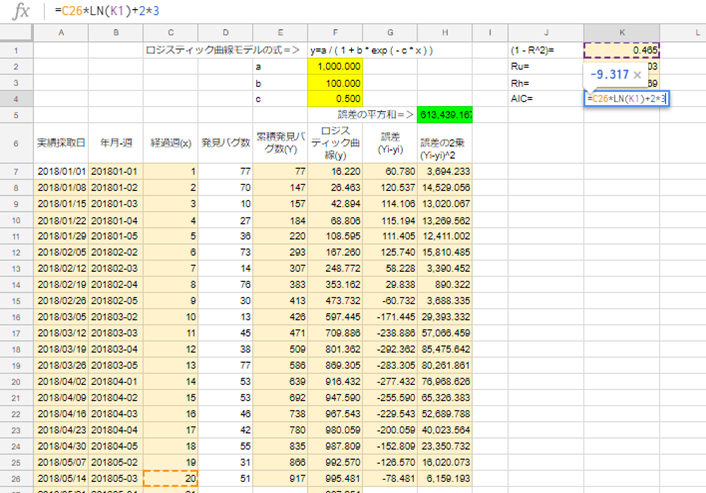
2.1.1. データと式の設定

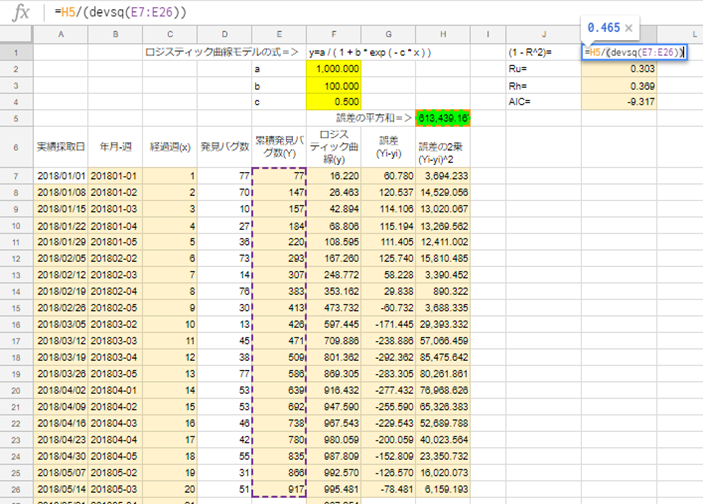
K1セルに「=H5/(devsq(E7:E26))」を入力。
※バグ実績の最終週(E26セル)までを範囲としています。ご利用の際には、この範囲を適宜変えてください。

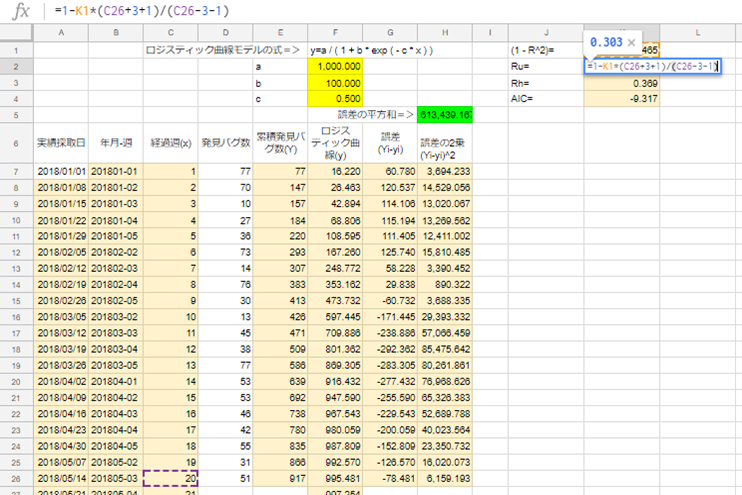
K2セルに「=1-K1*(C26+3+1)/(C26-3-1)」を入力。
※最終週(C26セル)を対象としています。ご利用の際には、ここを適宜変えてください。

K3セルに「=1-K1*(C26-1)*(C26+3+1)/((C26+1)*(C26-3-1))」を入力。

K4セルに「=C26*LN(K1)+2*3)」を入力。

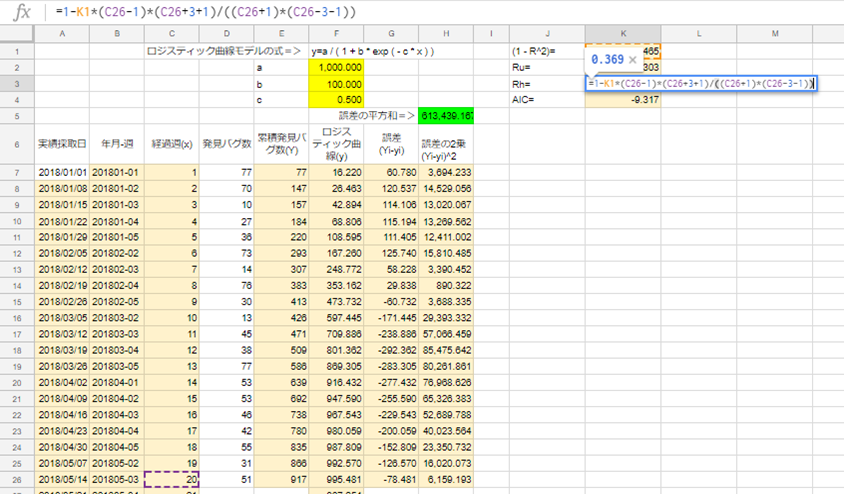
F2セルに「1000」、F3セルに「100」、F4セルに「0.5」を入力。
※このa,b,cの値は、この後「Solver」で最適な値に算出しなおされますので、大体の数字を入力しておきます。今回は20週目のバグ累積件数が917件なので、aは「1000」としました。bはその10分の1の「10」、cは適当の「0.5」。
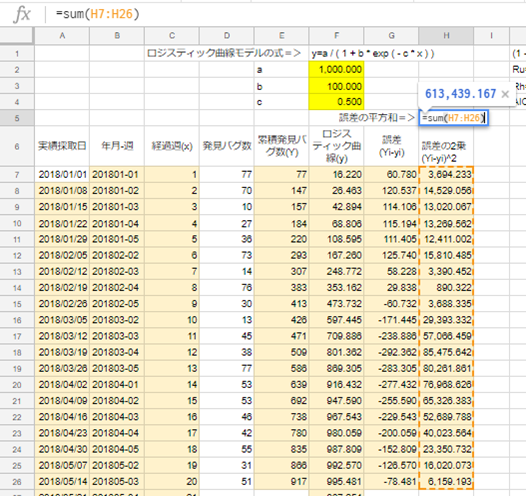
H5セルに「=sum(H7:H26)」を入力。

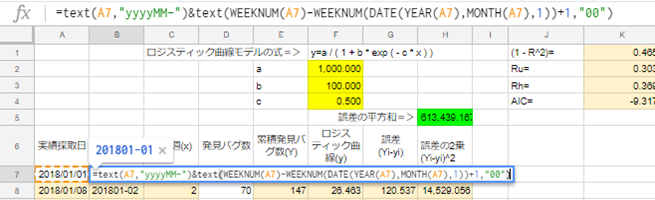
A7セルに実績採取を開始した日、この例では「2018/01/01」を入力し、A8セルからA106セルまでは、一つ上のセルに「+7」した式をずっと埋めます。
B7セルに「=text(A7,"yyyyMM-")&text(WEEKNUM(A7)-WEEKNUM(DATE(YEAR(A7),MONTH(A7),1))+1,"00)」を入力し、A7セルをコピーし、B8セルからB106セルまで式を貼り付けます。

C7セルに「1」を入力し、C8セルからC106セルまでは、一つ上のセルに「+1」した式をずっと埋めます。
D7:D26セル範囲に、発見したバグ件数を入力します。
E7セルに「=D7」を入力し、E8セルに「=F7+D8」を入力し、E8セルをコピーし、E9セルからE106セルまで貼り付けます(バグ数を週ごとに累積しています)。
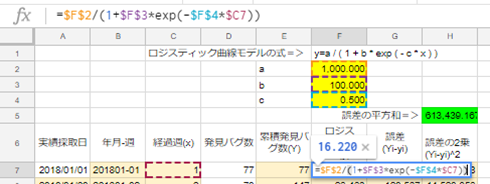
F7セルに「=$F$2/(1+$F$3*exp(-$F$4*$C7))」を入力し、F7セルをコピーし、F8セルからF106セルまで式を貼り付けます(ロジスティック曲線の式です)。

G7セルに「=E7-F7」を入力し、G7セルをコピーし、G8セルからG106セルに貼り付けます。

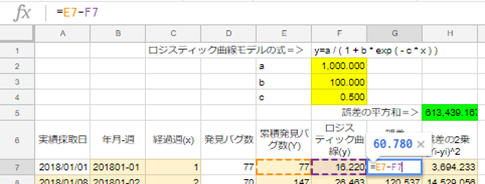
H7セルに「=G7^2」を入力し、H7セルをコピーし、H8セルからH106セルに貼り付けます。

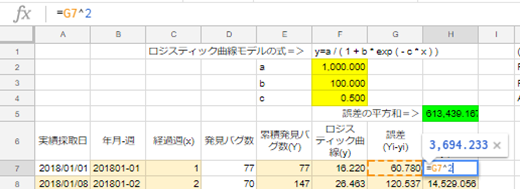
2.1.2. 「Solver」の実行

「メニュー」バーの「アドオン」メニューをクリックします。
「メニュー」アイテムから、「Solver-Start」をクリックします。

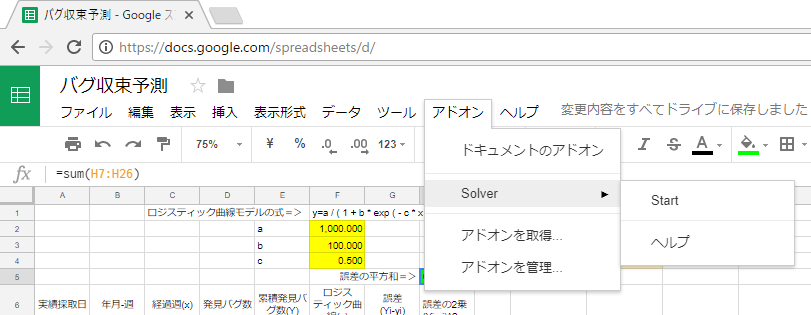
右サイドメニューに「Solver」のパラメータを設定する画面が表示されます。
「Set Objective:」(Excelソルバーで言うところの「目的セル」)に「H5」を入力。
「To:」(Excelソルバーで言うところの「目標値」)を「Min」に。
「By Changing：」(Excelソルバーで言うところの「変化させるセル」)を「F2:F4」を入力。
※H5セルは誤差2乗の合計。この値が最小(Min)になるように「Solver」がうまいことa,b,cの値(F2:F4)を変える。
「Solve」ボタンをクリックすると、計算が始まります。

計算が終わると次のようなダイアログが右下に表示されます。

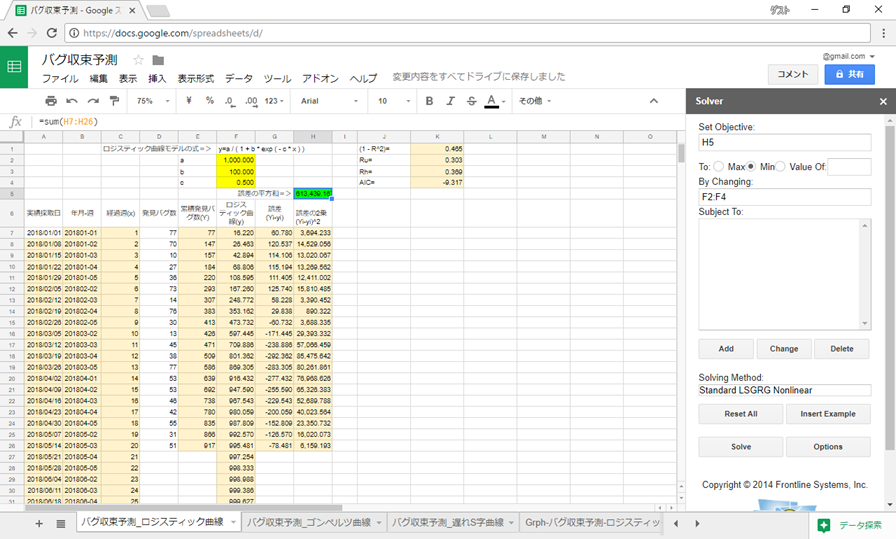
すると、a,b,cの値(F2:F4)が変わっています。
20週目(2018年5月3週)のバグ実績が917件。aの値が約1,148なので、今後1,148件まで成長する見込み。
56週目(2019年1月4週)で予測値が「1,147.582件」で四捨五入して1,148件。
大体この時期にバグが収束すると予測。

2.1.3.グラフ化

青の棒グラフが、バグの実績値(累積)。赤の棒グラフがロジスティック曲線で引いた予測です。

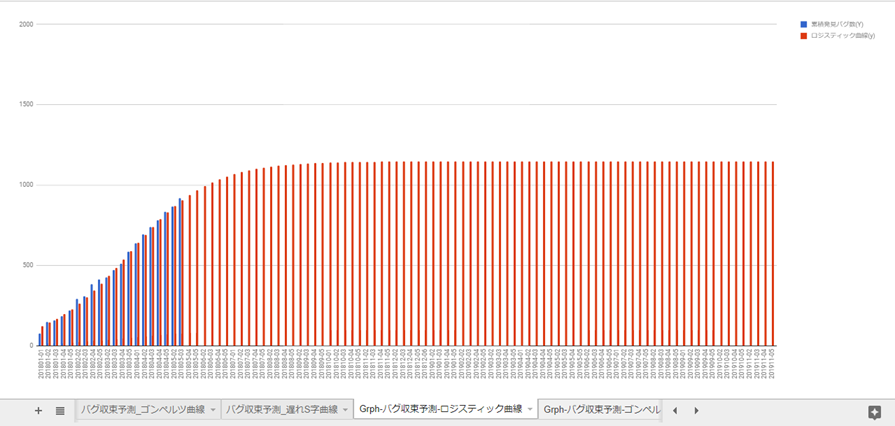
2.2. ゴンペルツ曲線

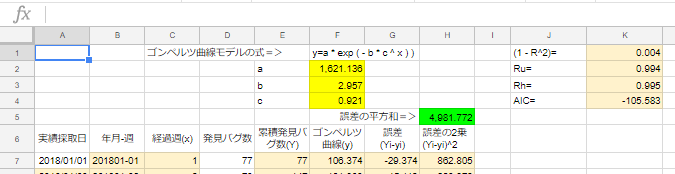
ゴンペルツ曲線モデルの式＝＞y=a*exp(-b*c^x)
ちょっと手抜き。

ロジスティック曲線で作ったシートをコピーして、ゴンペルツ曲線用のシートを作ります。

F7セルに「=$F$2*exp(-$F$3*$F$4^$C7)」を入力し、F7セルをコピーし、F8セルからF115セルまで式を貼り付けます(ゴンペルツ曲線の式です)。
※収束時期がずっとあとなので、A、B、C、Fの列の式を115行までコピーします。

ロジスティック曲線同様に「Solver」を使った結果、
すると、a,b,cの値(F2:F4)が変わっています。

aの値を見ると1,621.136件。四捨五入で今後1,621件まで成長する見込み。
109週目(2020年1月5週)で予測値が「1,620.521件」で四捨五入して1,621件。
大体この時期にバグが収束すると予測。

ロジスティック曲線と比べて、ゴンペルツ曲線で予測すると、今後発生するバグ数と収束時期がだいぶ違います。
どちらを選んだ方がよいでしょうか？それは3章でやります。

2.3. 遅れS字曲線

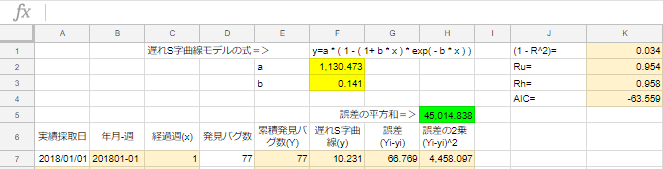
遅れS字曲線モデルの式＝＞y=a*(1-(1+b*x)*exp(-b*x))

ロジスティック曲線で作ったシートをコピーして、遅れS字曲線用のシートを作ります。
遅れS字曲線は、パラメータがa,bの2つなので、Ru、Rh、AICの式を少し変えます。
K2セル「=1-K1*(C26+2+1)/(C26-2-1)」
K3セル「=1-K1*(C26-1)*(C26+2+1)/((C26+1)*(C26-2-1))」
K4セル「=C26*LN(K1)+2*2」
F7セルに「=$F$2*(1-(1+$F$3*$C7)*exp(-$F$3*$C7))」を入力し、F7セルをコピーし、F8セルからF106セルまで式を貼り付けます(遅れS字曲線の式です)。

ロジスティック曲線同様に「Solver」を使った結果、
すると、a,bの値(F2:F4)が変わっています。

aの値を見ると1,130.473件。四捨五入で今後1,130件まで成長する見込み。
67週目(2019年4月2週)で予測値が「1,129.539件」で四捨五入して1,130件。
大体この時期にバグが収束すると予測。

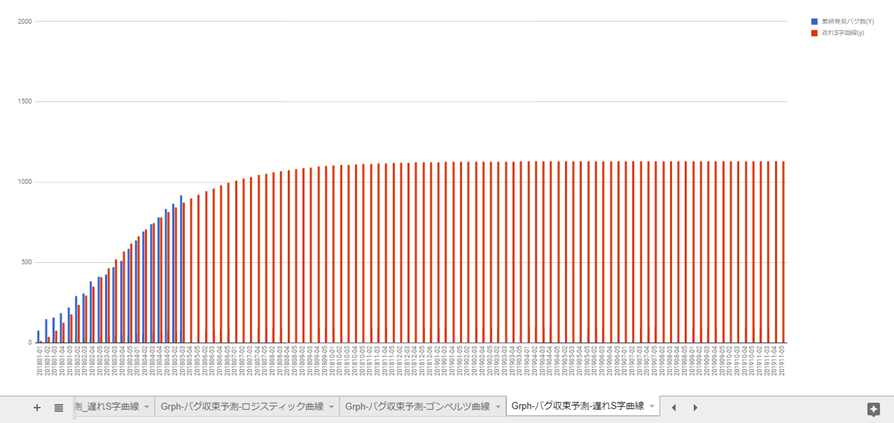
ロジスティック曲線、ゴンペルツ曲線と比べて、遅れS字曲線で予測すると、こちらも今後発生するバグ数と収束時期がだいぶ違います。

3. バグ実績件数と一番マッチしている成長曲線で将来を予測する。

難しい話はよくわからないですが、最適なモデルを選択する基準がいくつかあって、今回は、(1)上田選択基準(Ru)、(2)芳賀ほかの選択基準(Rh)、(3)赤池の情報量基準(AIC)で決めます。

3つの曲線のRu、Rhの値が最大で、AICが最小の曲線を選択します。
今回の例では、ゴンペルツ曲線がこれに該当します。

(1)上田選択基準(Ru)=1-(1-R^2)*(n+k+1)/(n-k-1)
(2)芳賀ほかの選択基準(Rh)=1-(1-R^2)*((n-1)*(n+k+1)/(n+1)*(n-k-1))
(3)赤池の情報量基準(AIC)=n*LN((1-R^2))+2*k
(4)(1-R^2)=誤差の平方和/実測値の偏差平方和=H5/(devsq(E7:E26))
n=データ件数
k=パラメータ(未知の係数)の個数

4.参考文献

Excelでできる最適化の実践らくらく読本―ソルバーで自由自在に解く 単行本 – 2003/6
苅田 正雄  (著),‎ 上田 太一郎  (著),‎ 中西 元子  (著)
単行本: 233ページ
出版社: 同友館 (2003/06)
言語: 日本語
ISBN-10: 4496035804
ISBN-13: 978-4496035807

※新版が出ている。