Big O notation
就活のためアルゴリズムやデータ構造の勉強を改めてやることにしました。今回 Big O 記法の勉強したのでそのまとめ。
まず、良いコードとは?
- Readable
- Scalable (Speed of runtime, Memory) -> Big O で測れる
コードを実行する際、それを実行するコンピューターの性能に依存するのではなく、プログラムそのものの性能を図るための指標として用いられる記法のこと。
Speed of runtime: インプット量が増える度に実行時間が比例してどのくらい増えるか(オペレーションの数が増えるか)
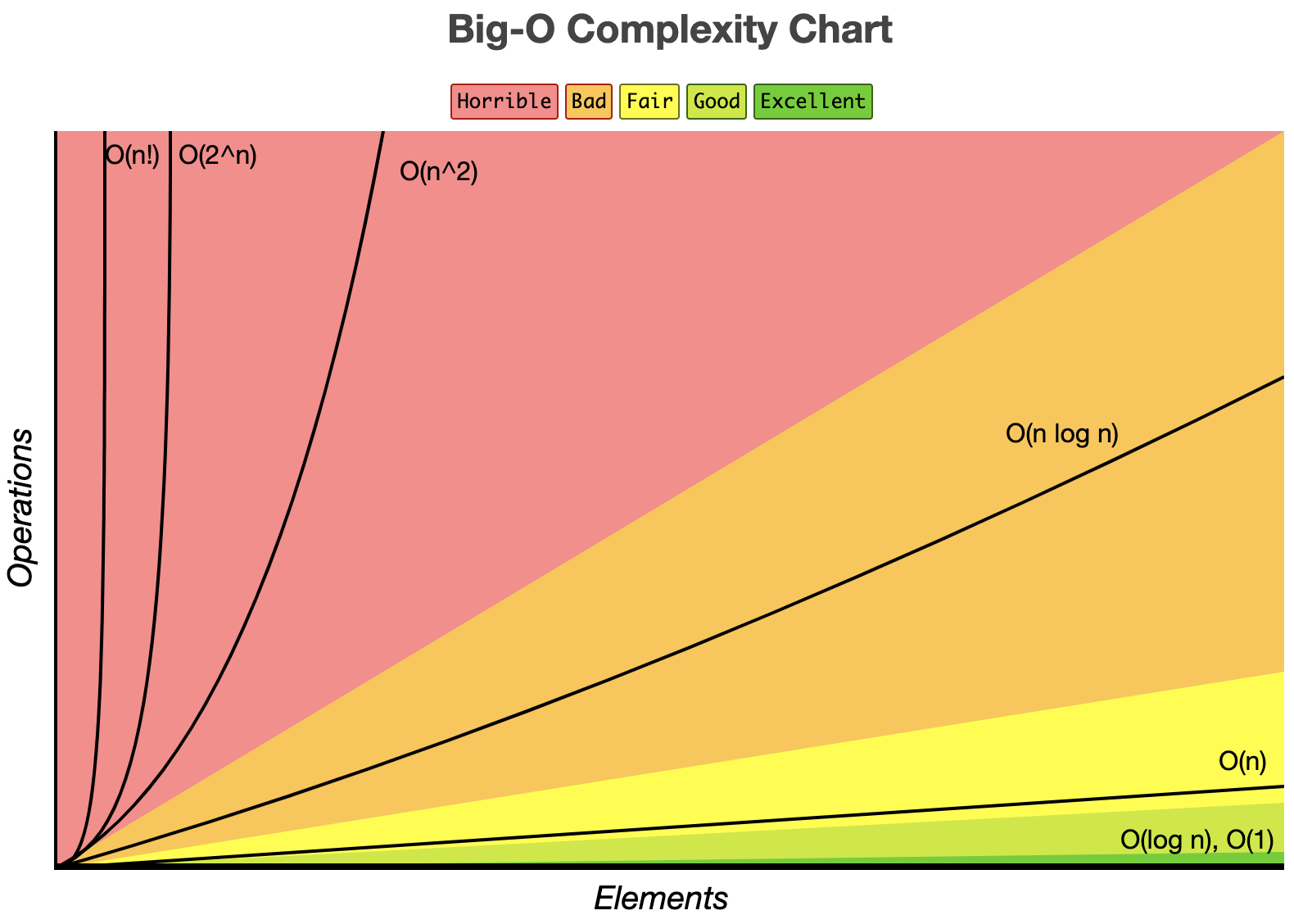
以下のチャートで、インプット数とオペレーションの数の関係がまとめられている。
プログラムを書く時、なるだけ Excellent になる Time Complexity を目指すべし。
基本
O(n) - Linear Time
インプットが増えるに伴い、オペレーションの数も比例して増える。
const arr = ['apple', 'banana', 'peach'];
function findApple(array) {
for (let i = 0; i < array.length; i++) {
if (array[i] === 'apple') {
console.log('Found Apple!');
// break ->見つけた時点で抜け出せるけど、最悪は最後までループするのでそのケースを想定
}
}
}
findApple(arr); // O(n) --> Linear Time
O(1) - Constant Time
インプットが増えてもオペレーションの数は変わらない。必ず2回のオペレーションステップでい続けるので、グラフの場合線は並行である続ける。
const boxes = [0, 1, 2, 3, 4, 5];
function logFirstTwoBoxes(boxes) {
console.log(boxes[0]); //O(1)
console.log(boxes[1]); //O(1)
}
logFirstTwoBoxes(boxes); // O(2) everytime -> O(1)
O(n^2) - Quadratic Time
ネストループ
// O(n^2)
const nums = ['a', 'b', 'c', 'd', 'e'];
function logAllPairsOfArray(array) {
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length; j++) {
console.log(array[i], array[j]);
}
}
}
Time Complexity を計算する上でのルールがある。
BIG O ルール
-
Worst Case
(例:ループだと、一致するものを途中で見つける可能性もあるが、最悪のケース、毎回最後までループしなければいけないケースを想定する)
-
Remove Constant
(例:2n+ 100) -> O(n)となる。 より多くのインプット量を想定したとき、誤差の範囲内になる)
-
Different terms of input
(例:input が複数の場合。O(a + b) or O(a*b)と、Big O もそれぞれ用意。
-> same indentation-> add
-> anything different -> multiply というのが簡単な計算方法。
-
Drop Non Dominants
(2 と同じ考え方)
まとめ
O(1) Constant
- ループなし
O(log N) Logarithmic
- 通常は、Binary SearchなどのSearching AlgorithmsがO(log N) (ソートされてる前提)
O(n) Linear
- n回for loopやwhile loopsを行う
O(n log(n)) Log Linear
- 大抵はSorting operation
O(n^2) - Quadratic
- コレクション内のすべての要素を比較する、 two nested loops
O(2^n) - Exponential
- Nサイズの問題を解決するrecursive algorithm
O(n!) - Factorial
- すべての要素にループを追加
実行時間だけではなく、メモリの使用量もBig O で測ることができる。
Space Complexity
2 ways of storing memory
Heap: store variables that are assigned
stack: function calls
参考
こちらのUdemyで勉強しています。
Master the Coding Interview: Data Structures and Algorithm
グラフの参考はこちらのサイトです。
Big-O Cheat Sheet